こんにちは！
JR「山科」駅から徒歩3分！
京阪「山科」駅から徒歩3分！
京都市営地下鉄東西線「山科」駅 徒歩10秒！
“逆転合格”の「武田塾山科校」です！
山科校は、京都府宇治市、京都市伏見区・南区・中京区・上京区・山科区、長岡京市、向日市、大山崎町、滋賀県大津市など近隣の県からも通塾いただけます。
武田塾には京都大学・大阪大学・神戸大学等の
国公立大学や、早慶上理、関関同立、産近甲龍
といった難関私立大学に逆転合格を目指して
通っている生徒が数多く在籍しています！
今回は苦手とする人が多い円運動について、取り上げたいと思います。
特に遠心力について、よくわかっていない人が多いのではないでしょうか？
まずはこの問題から！
まずはこの問題を解いていきましょう！
すでに学校の授業などで、円運動について勉強していて色々と混乱している人がいるかもしれませんが、
習ったことは一旦忘れてフレッシュな気持ちでこの問題と解説を読んでみてください！
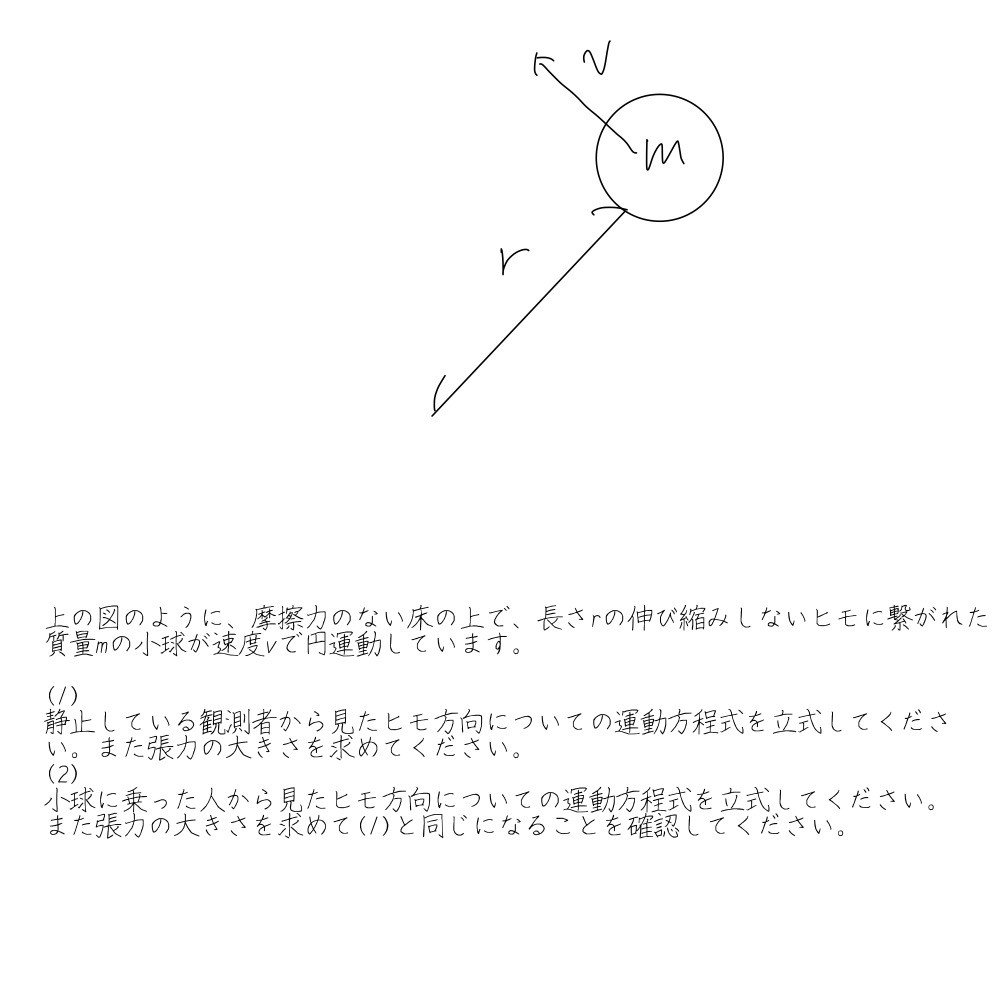
この問題はツルツルな床の上でひもに繋がった小球が円運動をするという問題です。
(2)で遠心力が登場するのですが、一旦（１）を解いてみましょう！
まずは…
これは全ての力学の問題について言えることですが、力学の問題を解くプロセスは、、、
①ある軸上についての力を考える。（未知の場合はTなどの文字でおく）
②その物体の加速度を考える。（未知の場合はaなどの文字でおく。この場合がほとんど）
③運動方程式をたてる。
の3ステップです。一つずつやっていきましょう！
①
まずは力の図示です。
今回考える軸は円の中心方向に向かう軸です。
力には大きく分けて二つの種類があります。
接触力…張力、垂直抗力などの直接手や物で物体に触れて加える力
非接触力…重力、静電気力などの何も触れていないのに働く力。
今回は円の中心向きの方向に働く力は
接触力…張力
非接触力…なし（水平方向に重力は働かないので）
です。張力に関しては未知なので、Tとおきます。
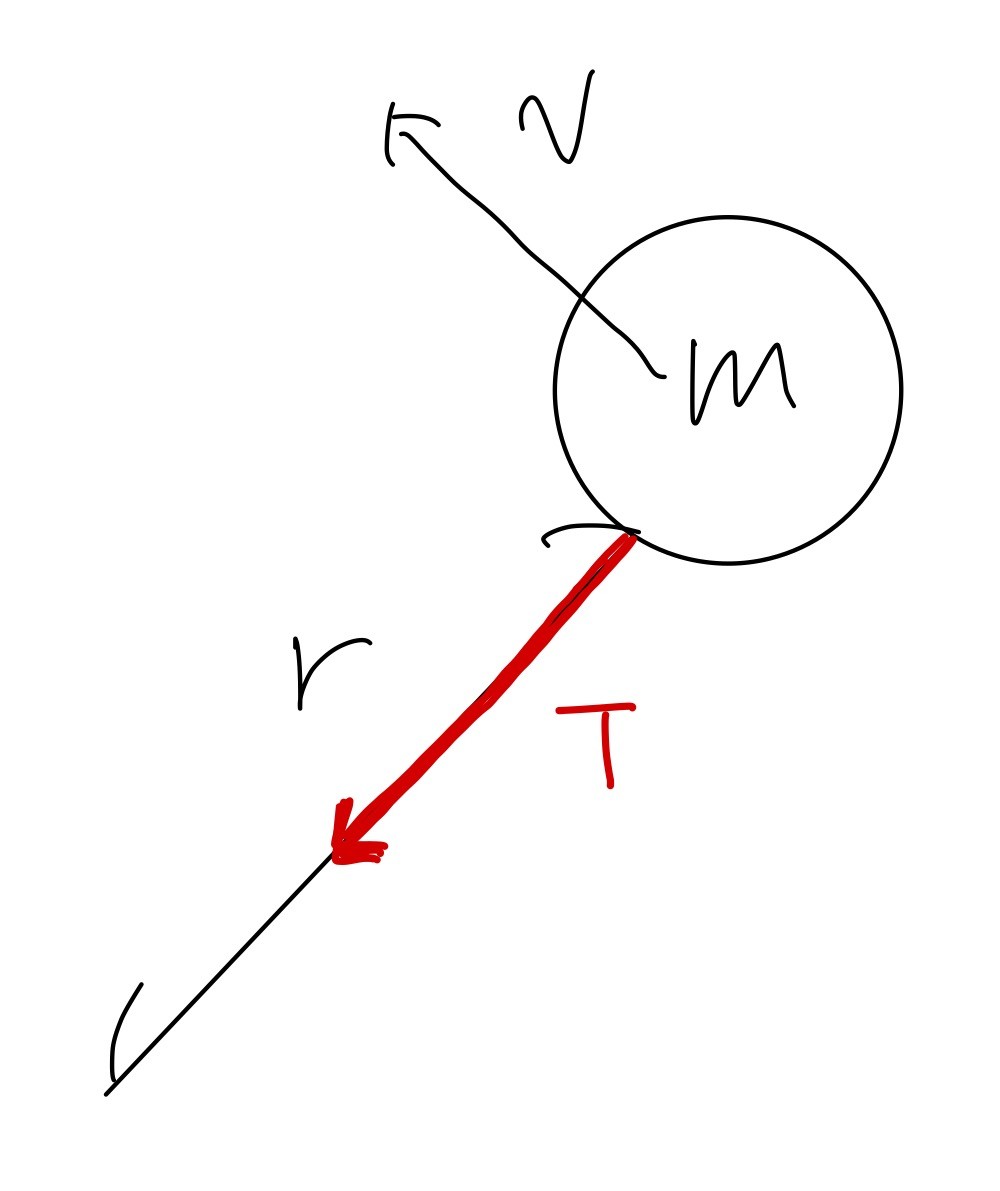
②
次は物体のある軸上についての加速度を考えます。
多くの人はあまり意識せずとりあえず「ma=～」と書いているのではないでしょうか？
本来考えるべきなのは、
運動方程式を立式する上で加速度の情報が必要→しかしながら未知数なので「a」でおく。
ということなのです。
ということで、この問題に関しても円の中心方向についての加速度を考えていきます。
今回に関しても未知数なので、aとおくのかと思いきや、実は円運動に関しては
半径と速度さえわかっていれば、加速度がわかってしまいます。
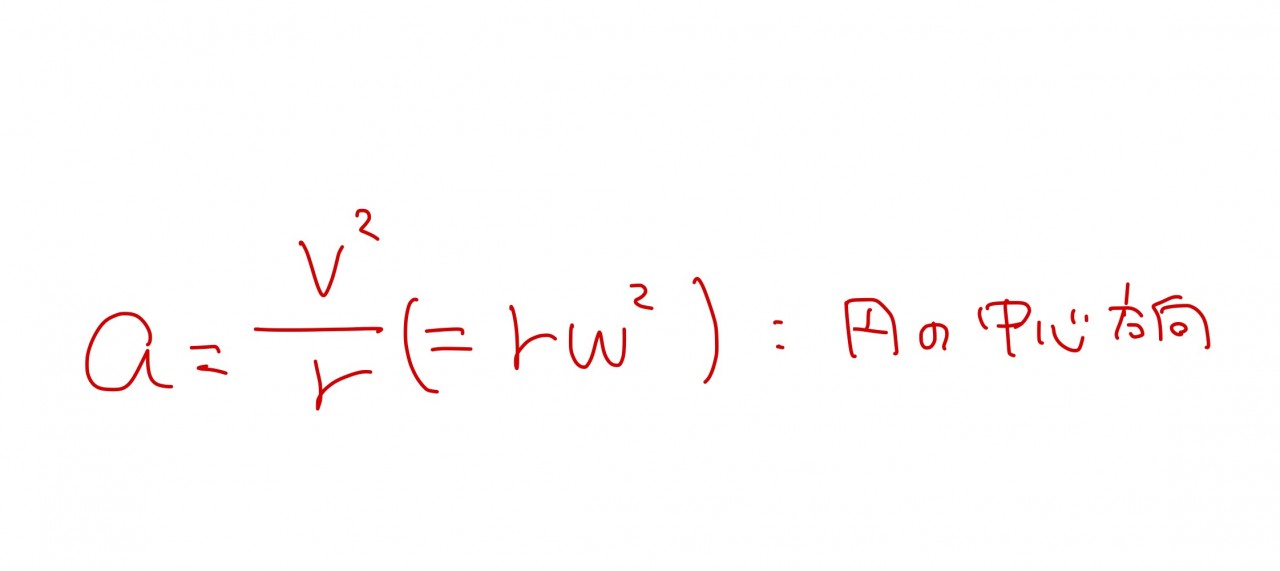
ここで注意して欲しいのは、等速円運動している物体は常に円の中心に向かって加速し続けているということです。
なかなかイメージが湧きにくいかもしれませんが、
車でその場をグルグルと回ることをイメージしてください。
ハンドルを回さないともちろんそのまま直進してしまうことになるので、ハンドルを常に円の中心方向に回して
曲がり続ける必要がありますよね？（たとえば反時計回りをしたいのなら常に左に曲がり続ける必要があります。）
常に曲がり続ける→円の中心方向に向かって速度が変化している→円の中心に向かって加速度が発生している
ということになります。頑張ってイメージできるようになりましょう！
何はともあれ円の中心方向の加速度は求めることができました。
③
力と加速度を求めることができたので後は運動方程式を立てましょう！
運動方程式を立てれば未知数のTも求めることができるはずです！
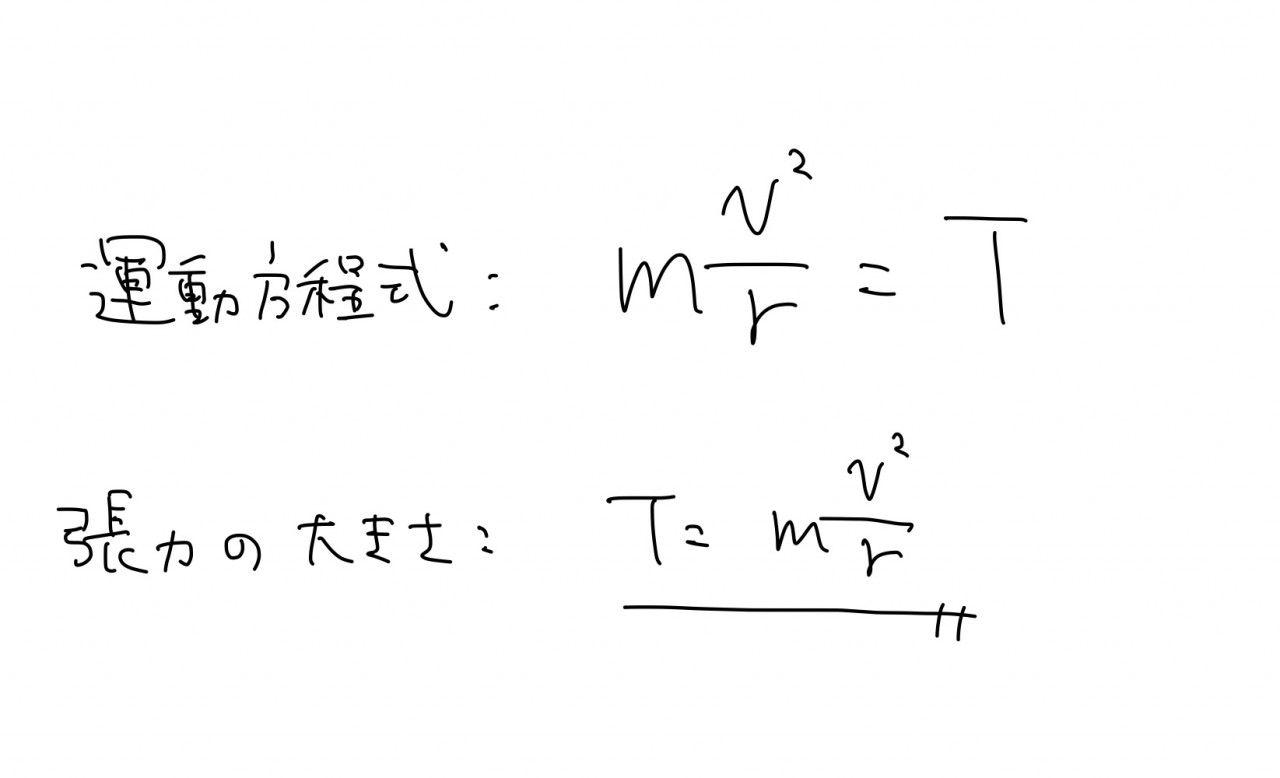
遠心力って？？
次は(2)を解いていきましょう！
まずは観測者が立っている場所を考えましょう。
先程も述べたように円の中心方向に向かって加速していますよね？
加速している人から見た運動方程式を立てるときは注意が必要です。
下の図のような加速度Aで加速している電車を考えてみてください。
この電車の中にあるボールは電車の中の人から見ると左に動いているように見えるはずです。
（電車が発車するときをイメージするとわかりやすいです。進行方向と逆向きによろけてしまうのではないでしょうか？）
さて水平方向の運動方程式をたててみましょう。
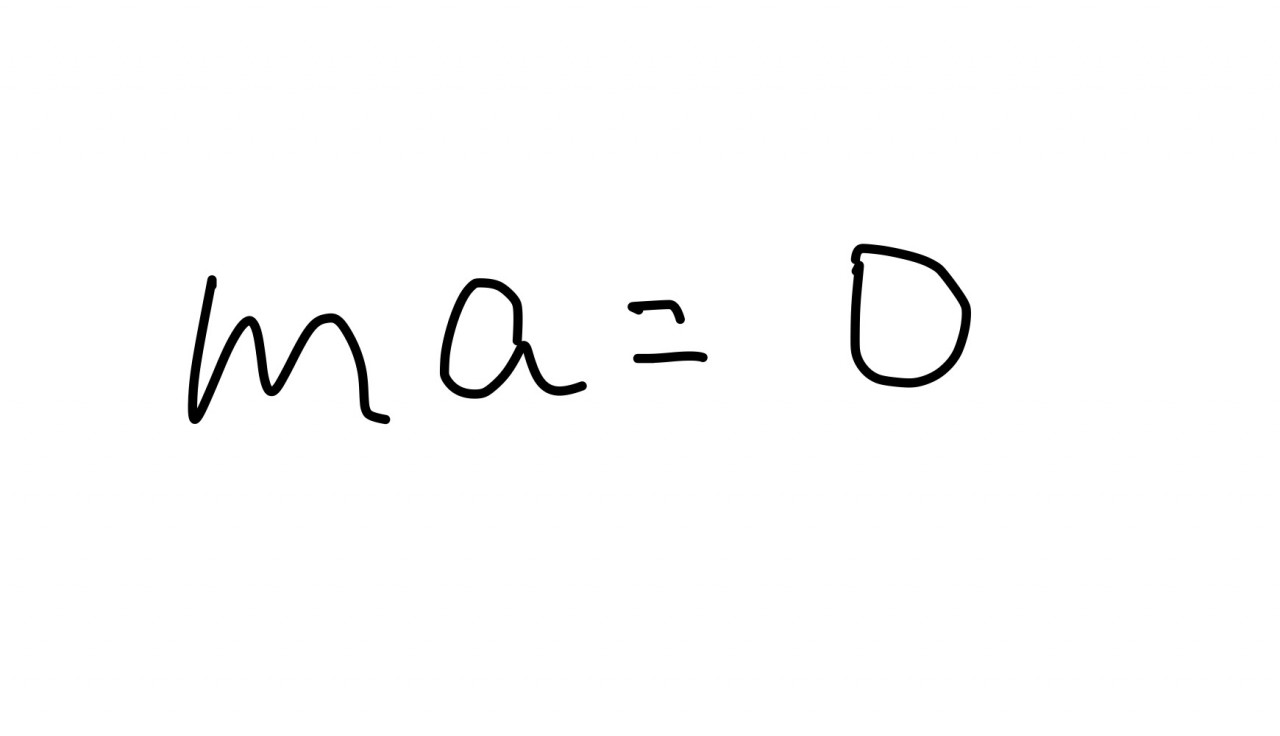←これはおかしい！！！！
水平方向の力は、誰も触っていないし、重力などの非接触力も当然はたらいていないので、0です。
よって水平方向の加速度は0になるので、ボール速度はずっと０、つまり止まっているように見えるはずです。
ですが実際には左に動いているように見えます。
運動方程式の言うことは絶対なので、運動方程式の立て方に問題があったということになります。
加速度がある観測者（速度ではないです！）が立てる運動方程式は、その加速度とは逆向きの方向に慣性力が働くと考えます。
その慣性力の大きさは物体の質量をm観測者の加速度をAとして、mAです。
つまり観測者からみた運動方程式の立式は以下のようになります。
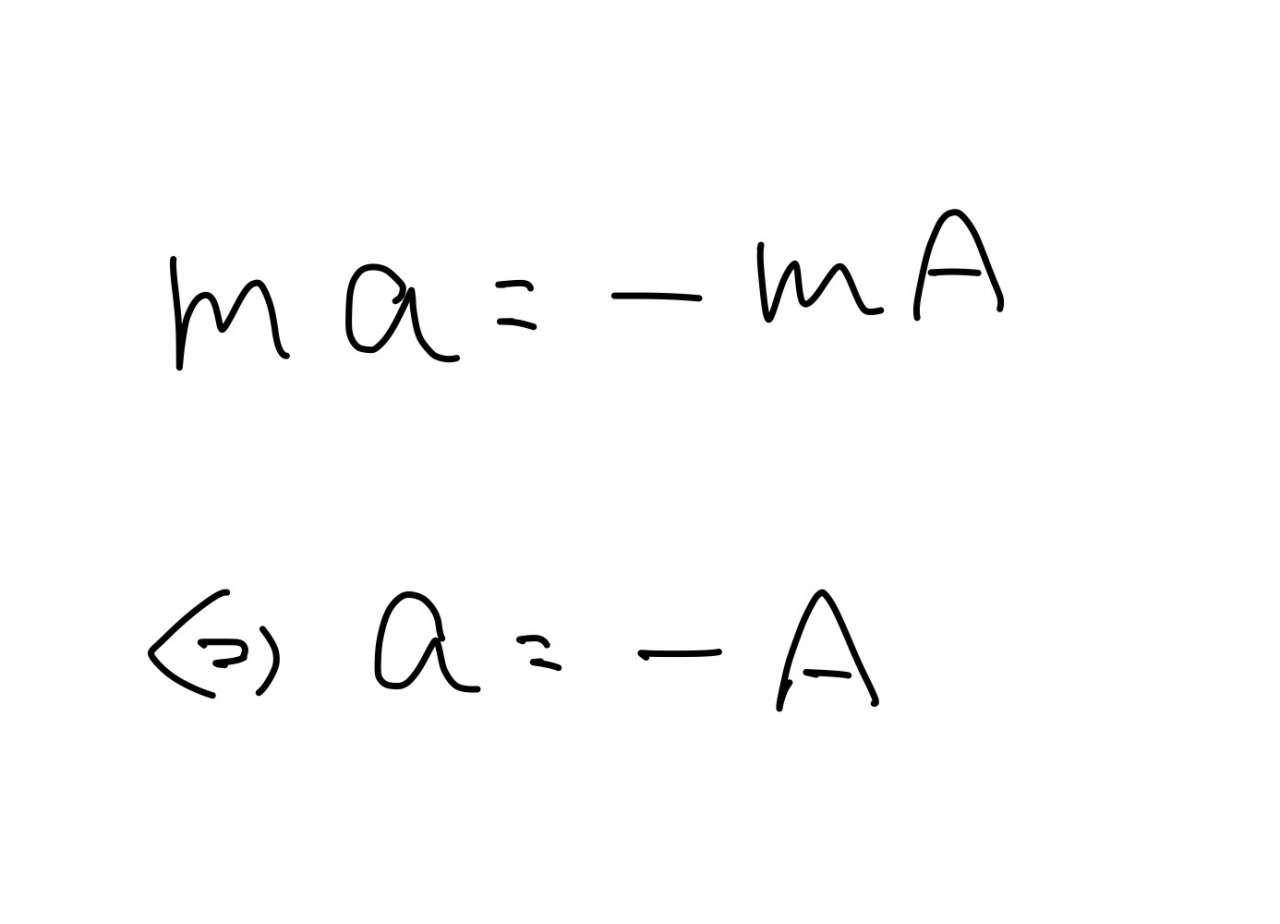
これは左向きに加速しているということになり、正しそうです。
ちなみに電車の外から電車の中を見ている人がこのボールについて運動方程式を立てると、
当然慣性力を考える必要はないので、ma=0のようになりボールは静止しているように見えているはずです。
電車の中から見ている人にとっては左向きに加速しているように、電車の外から見ている人にとっては静止しているように見えている
ということになり、どちらも正しいのです。
同じことを次は電車の中で立っている人について考えてみましょう。（人の体重はｍ[kg]とします。）
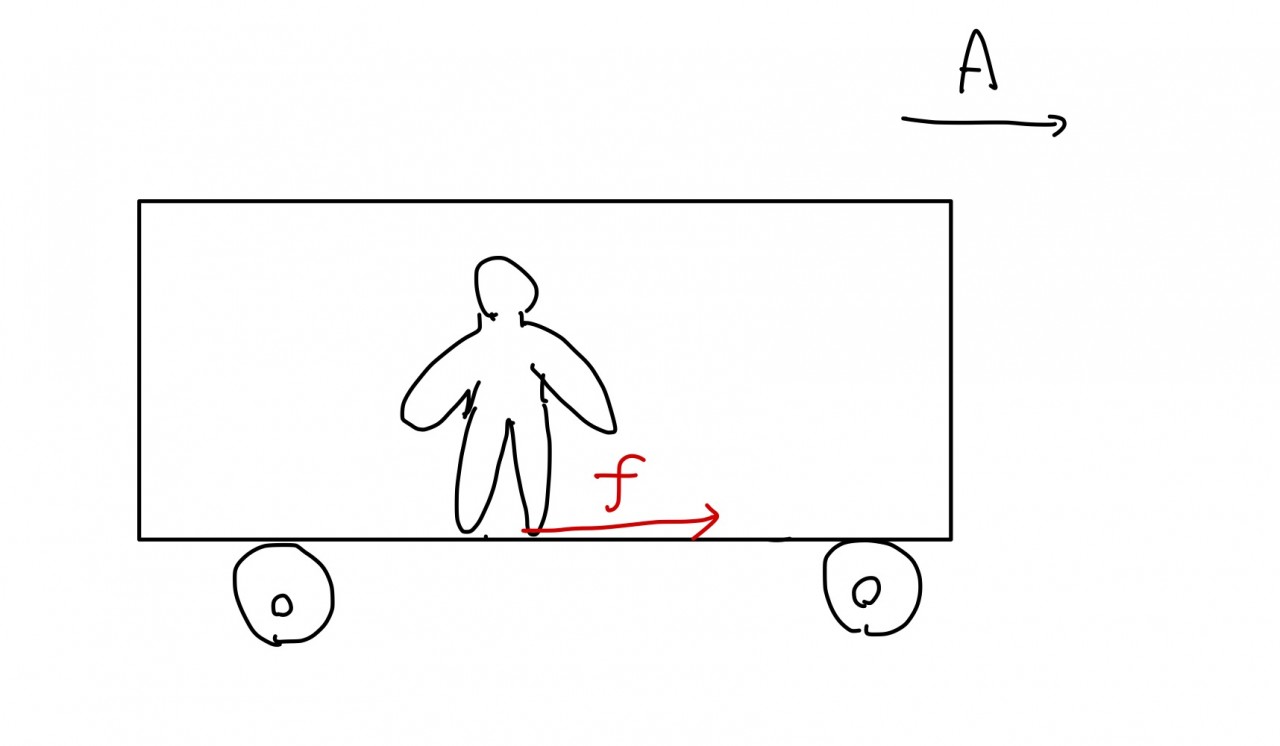
人は通常靴を履いて外に出るため、電車と人の間には摩擦力が働きます。
まずは観測者が電車の中の人である場合を考えましょう。
前述したような慣性力を考えて、また摩擦力をfとして、運動方程式は以下のようになります。
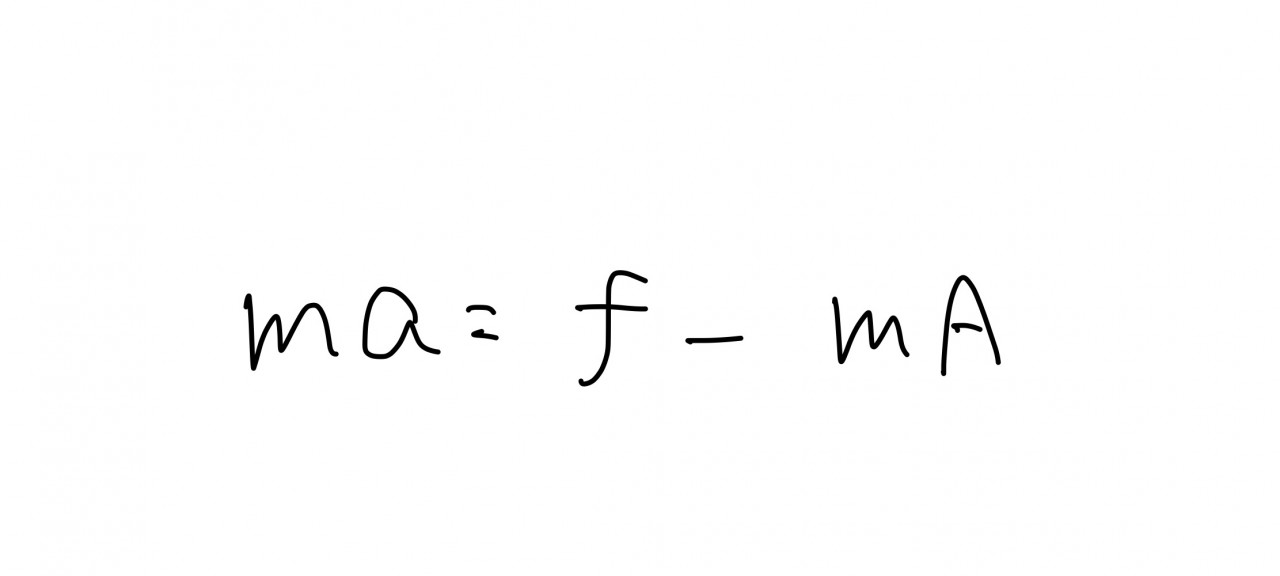
電車の中の人から見ると、人は止まっているように見えるはずなのでa=0なのでf-mA=0
よってf=mAであることがわかるはずです。
次に電車の外にいる人の場合です。
今度は慣性力を考える必要はないので、運動方程式は以下のようになります。
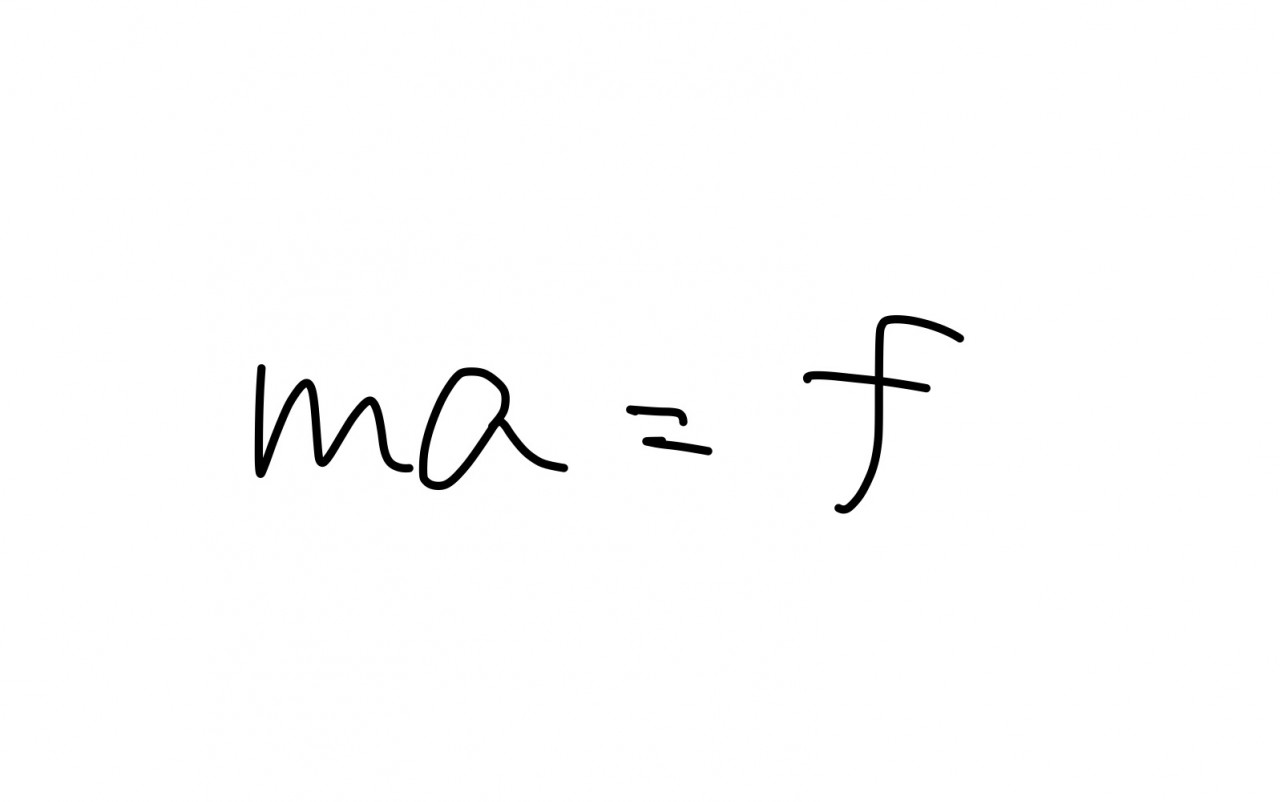
こちらについては電車の外にいる人から見れば、電車と同じ加速度Aで加速しているように見えるはずなので、ma=mA=f
つまりｆ＝mAであることがわかるはずです。
どうでしょうか？加速度のある観測者からみた運動方程式については慣れてきましたか？
それでは本題の(2)についても、まったく同じように運動方程式を立ててみましょう。
円運動は中心向きに加速し続けている運動なので、慣性力は中心から遠ざかるように働いていると考えて運動方程式は以下のようになります。
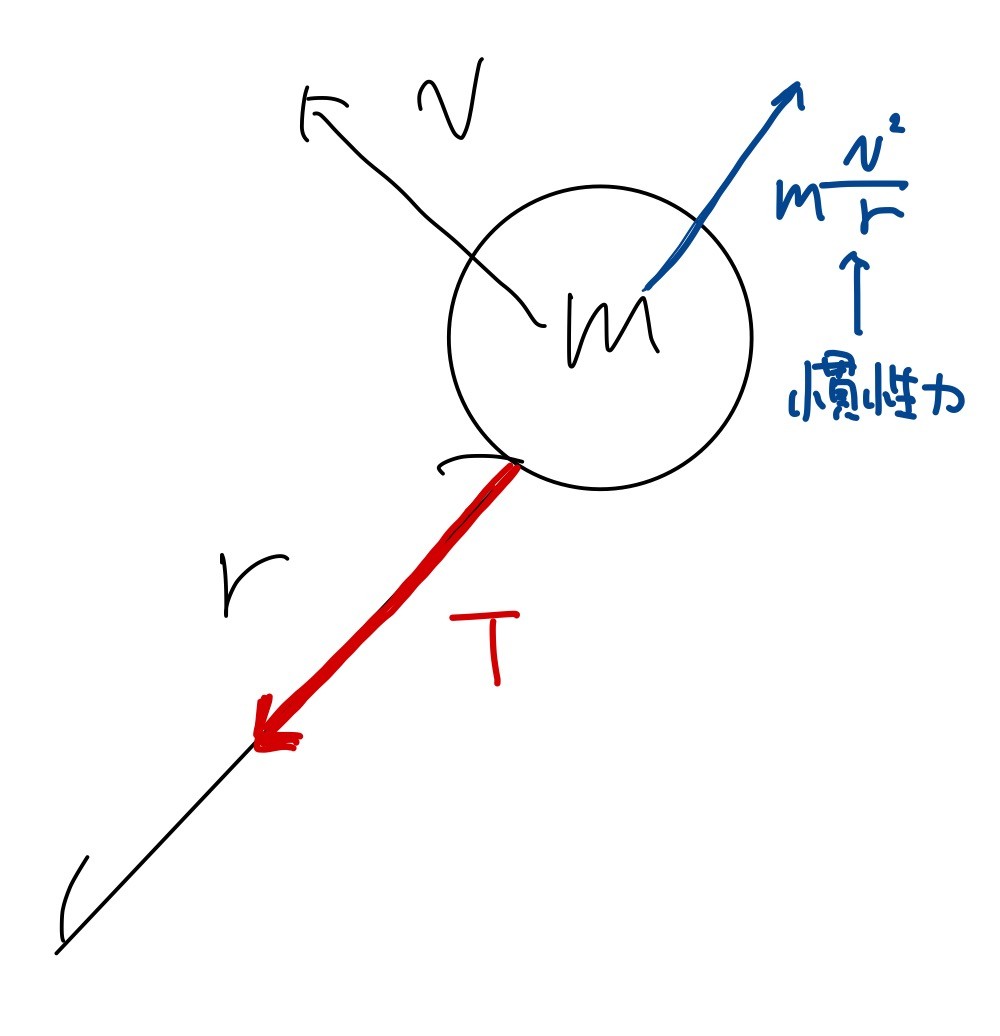
ちなみにこの慣性力のことを遠心力と言います。
遠心力といっても難しいことは何もなく、観測者が加速しているので、運動方程式に補正を加えているだけであることがわかっていただけたでしょうか？
まとめ
なにかと難しいとされている円運動ですが、結局押さえておくべきポイントは、
①円運動している物体の加速度は初めから分かっている！
②加速度のある観測者が運動方程式を立てるときは、慣性力を考える必要がある！
たったの２つだけです。
このブログを読んでポイントを理解できたら、ぜひ今までなんとなく解いてきた問題集にもう一度取り組み、
「意外と円運動って簡単！」と思えるようにしましょう！
勉強方法、参考書の使い方、点数の上げ方、なんでも教えます ★無料受験相談★受付中★
・模試で思うような結果が出なかった
・他塾のやり方が合わず成績が上がらない
・そもそも受験勉強って何をすればよいのかよくわからない、、、
などなど、受験に対する悩みは大なり小なり誰でも持っているもの。
どんな悩みでもOKです。持ってきてぶつけてください！
受検相談では、、、
- 奇跡の逆転合格プログラム
- 1日で英単語を100個覚える方法
- 志望校合格までのすべて
などなど、100％受験に役立つ情報をお話しします！！
ここまで聞いて、ひとりでできそうなら入塾しなくて構いません！
ぜひ一度ご来校ください！
お申し込みは、下記の無料受験相談フォームにご入力いただくか、
075-606-1381までお気軽にお問合せください！！
