こんにちは!
JR「山科」駅から徒歩3分!
京阪「山科」駅から徒歩3分!
京都市営地下鉄東西線「山科」駅 徒歩10秒!
“逆転合格”の「武田塾山科校」です!
山科校は、京都府宇治市、京都市伏見区・南区・中京区・上京区・山科区、長岡京市、向日市、大山崎町、滋賀県大津市など近隣の県からも通塾いただけます。
武田塾には京都大学・大阪大学・神戸大学等の
国公立大学や、早慶上理、関関同立、産近甲龍
といった難関私立大学に逆転合格を目指して
通っている生徒が数多く在籍しています!
交流回路とは?
主に電磁気分野の後半に扱う分野で、最も苦手とする人が多い分野でしょう。
なぜなら、電圧の値が時間変化してしまうからです!
「電源の電圧をV(t)=Vosinωtとする。」という問題に出会ったことはないでしょうか?
これは電圧がVoから-Voの間を三角関数的に変化することを表しています。
普通皆さんが電磁気分野を始めたての頃に出会う問題は電源の電圧はVで一定でしょう。
電圧が変化する方を交流、電圧が変化しない方を直流と言います。
実はコンセントは交流です。なぜ直流ではなく交流を使っているのか気になる人はネットで調べてみてください。
二コラ・テスラという人物に行きつくはずです(笑)
それはさておき、そんな電圧が変化してしまう交流回路難しく感じる人も多いのではないでしょうか?
確かに難しいかもしれませんが、公式を丸暗記せずにこれから書いていくプロセスに従って解いていけば簡単に解けるようになるはずです。
これを読むと出来るようになること
①コンデンサー、コイル、抵抗の電圧、電流が求めることができるようになる。
②インピーダンスを求めることができるようになる。
という感じです。消費電力などについても電流と電圧が判明しているので簡単に求めることができますね!
まずは知識のおさらい
みなさんは、電流Iが流れているコイル、抵抗、電荷Qが溜まっているコンデンサーに発生している電圧を求めることができますか?
覚えることは3つだけですが、逆に覚えていないと電磁気の問題は解くことができないので、ここで確認しておきましょう。
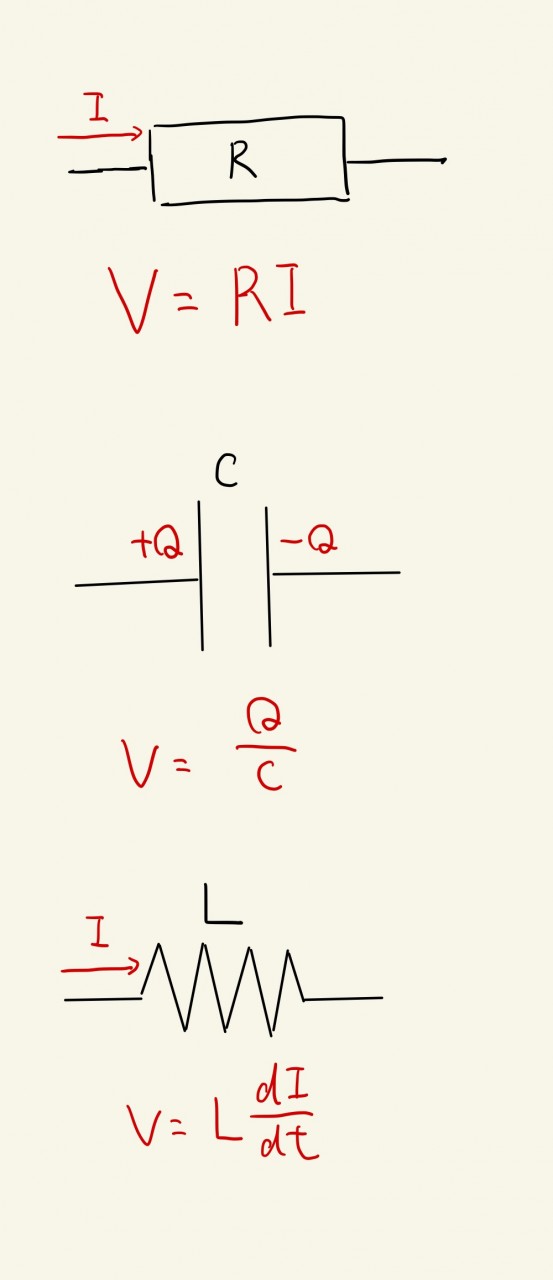
また電荷と電流に成り立つ公式も確認しておきましょう。
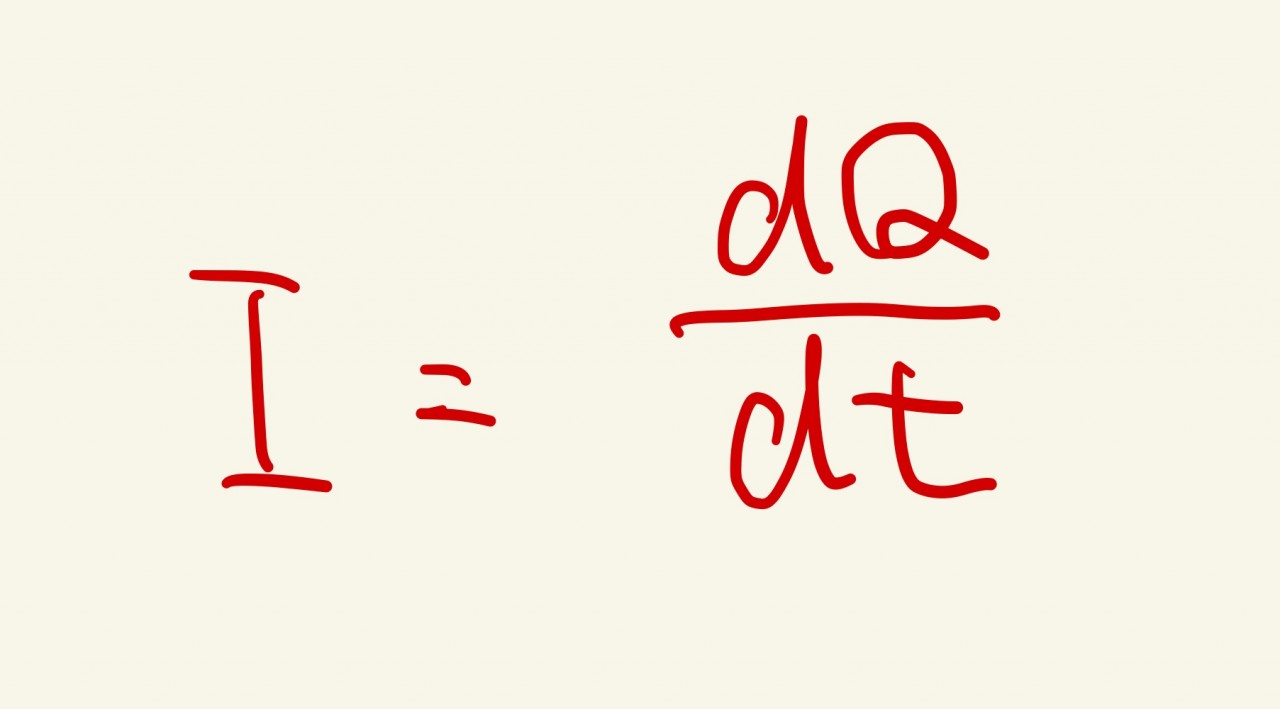
少し難しいかもしれませんが、そもそも電流の定義は一秒間あたりに流れる電荷です。
ということは微小時間Δt秒間電流Iがコンデンサーに流れ込んだらコンデンサーの電荷はIΔt[C]増加しますね?
これが電荷の増加量ΔQと一致するということになります。
Δをdに書き換えると上の公式を導出することができます。これは電荷を時間で微分すると電流になるということを意味します。
物理で微分と聞くと少し身構えてしまうかもしれませんが、数学でやった微分を思い出しましょう。
yをxで微分すると傾きを求めることができたと思います。傾きというのはxを少し増やしたときのyの増加量を
表しましたね?このxをIに、yをQに置き換えて考えれば、すんなり理解することができるはずです。
次に
では、今度は電流Iosinwtがコンデンサー、コイル、抵抗に流れ込むときに発生する電圧の大きさを求めてみましょう。
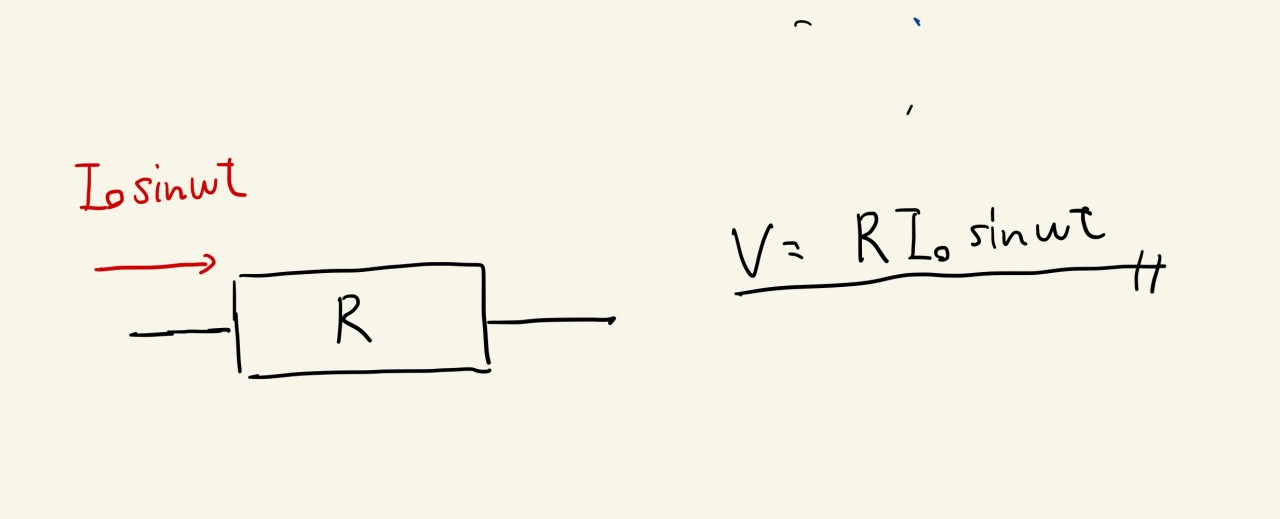


どうでしょうか?
ここで一つ気が付くことがあるはずです。sinの中身(つまりωtのことです。)のことを位相といいますが、
抵抗の位相は電流と電圧で一致していますが、コンデンサーに関しては電圧の位相が電流の位相に比べてπ/2進んでおり、
逆にコイルに関しては電流位相が電圧の位相に比べてπ/2だけ進んでいることがわかるはずです。
またオームの法則がV=RIであることを考えると、コイルの抵抗として機能している値はωL、
コンデンサーの場合は1/ωCであることがわかるはずです。(見かけの抵抗と呼んだりリアクタンスと呼んだりします。)
つまり、電流の値からコンデンサーやコイルに生じる電圧の値を求めたいのならば、
①位相を調節する。
②見かけの抵抗をかける。
のようにすればいいことがわかります。
ここまで読んでみて微分がどうしてもわからない!という人はこれを覚えてしまいましょう!
下に表にしてまとめてみます。
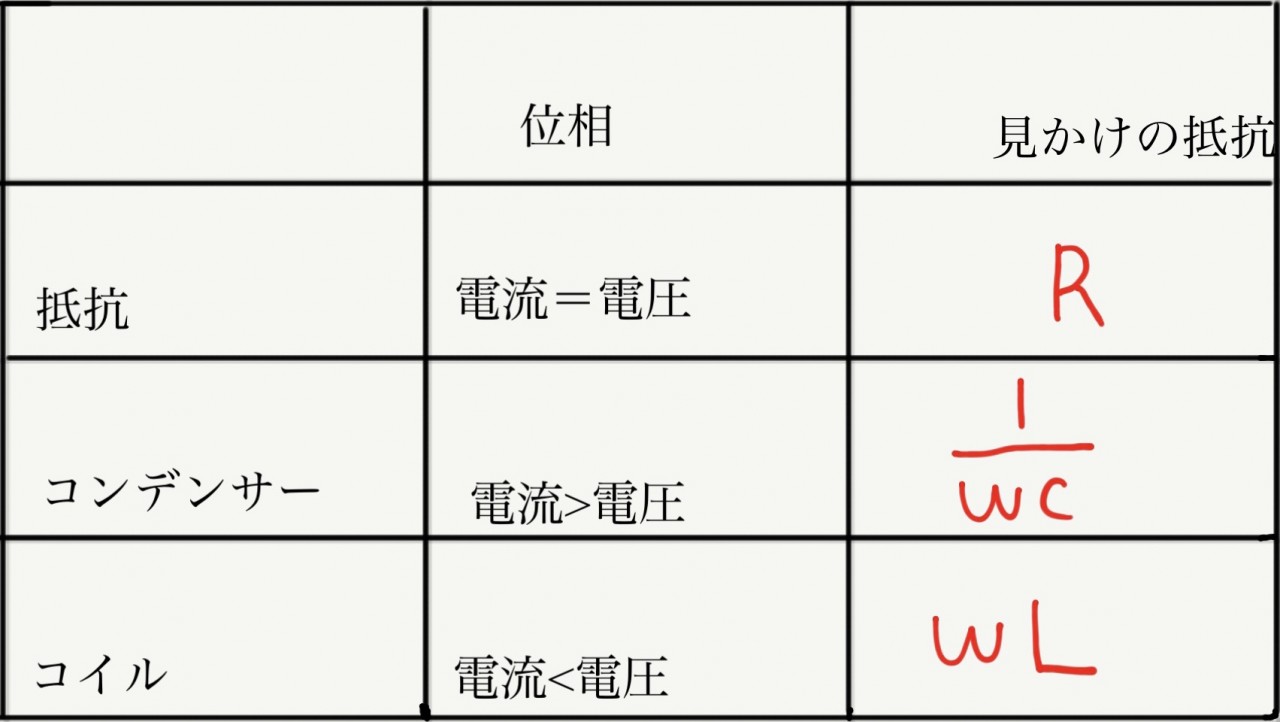
問題を解きながら復習してみよう!
では下のような回路図を考えます。
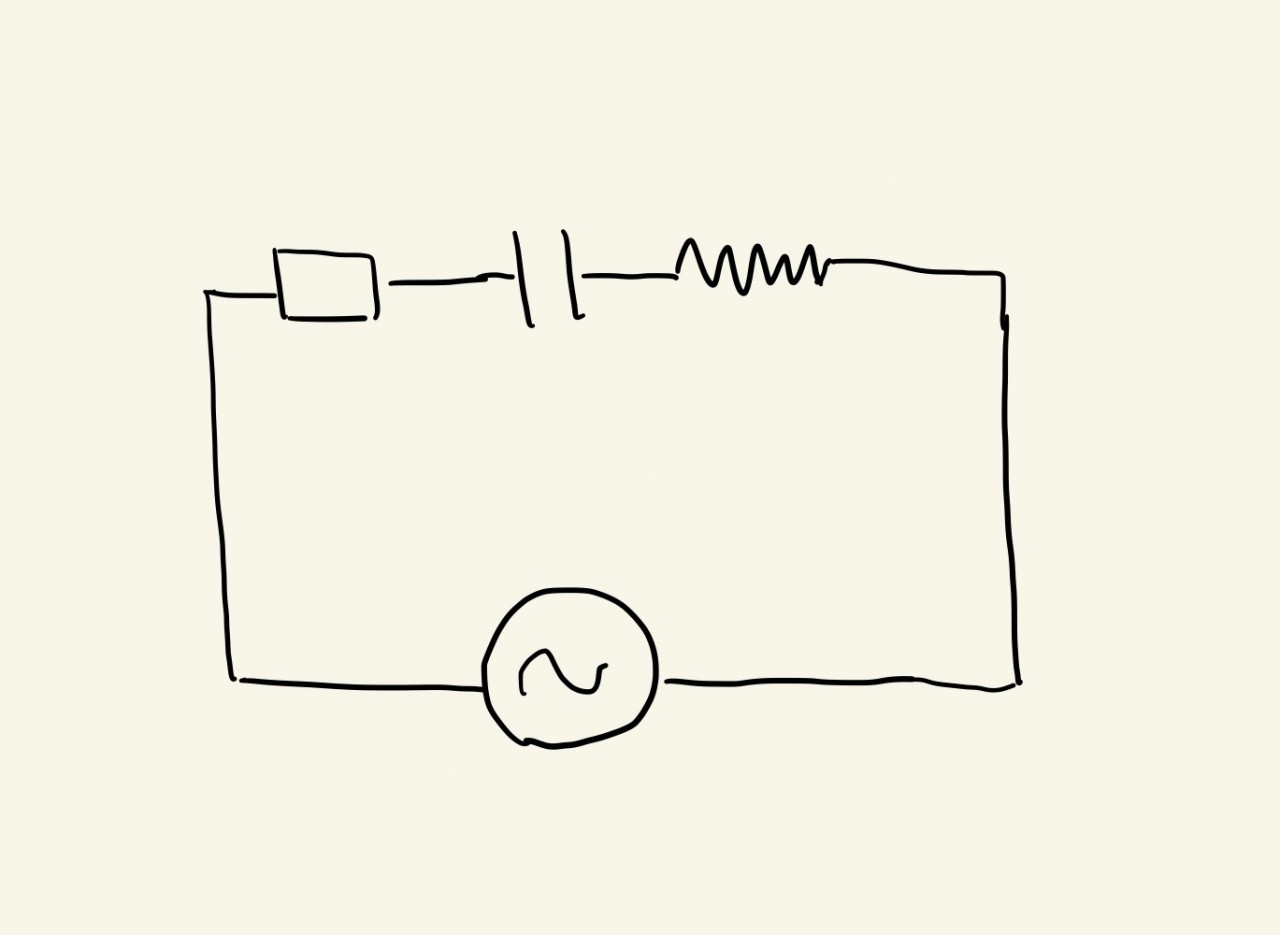
次のステップに従って解いてみましょう。
①電圧か電流の値をおく。直列つなぎなら電流の値を、並列なら電圧の値をおく。
②コンデンサー、コイル、抵抗に発生する電圧を求める。
③キルヒホッフの第二法則を立式する。
④図をかいて電圧や電流の値を決める。(必要があれば)
④については三角関数の合成でやっても良いのですが、少し計算が難しいです。
そこで簡単に図で書ける方法でやりたいと思います。
まずは①から③です!
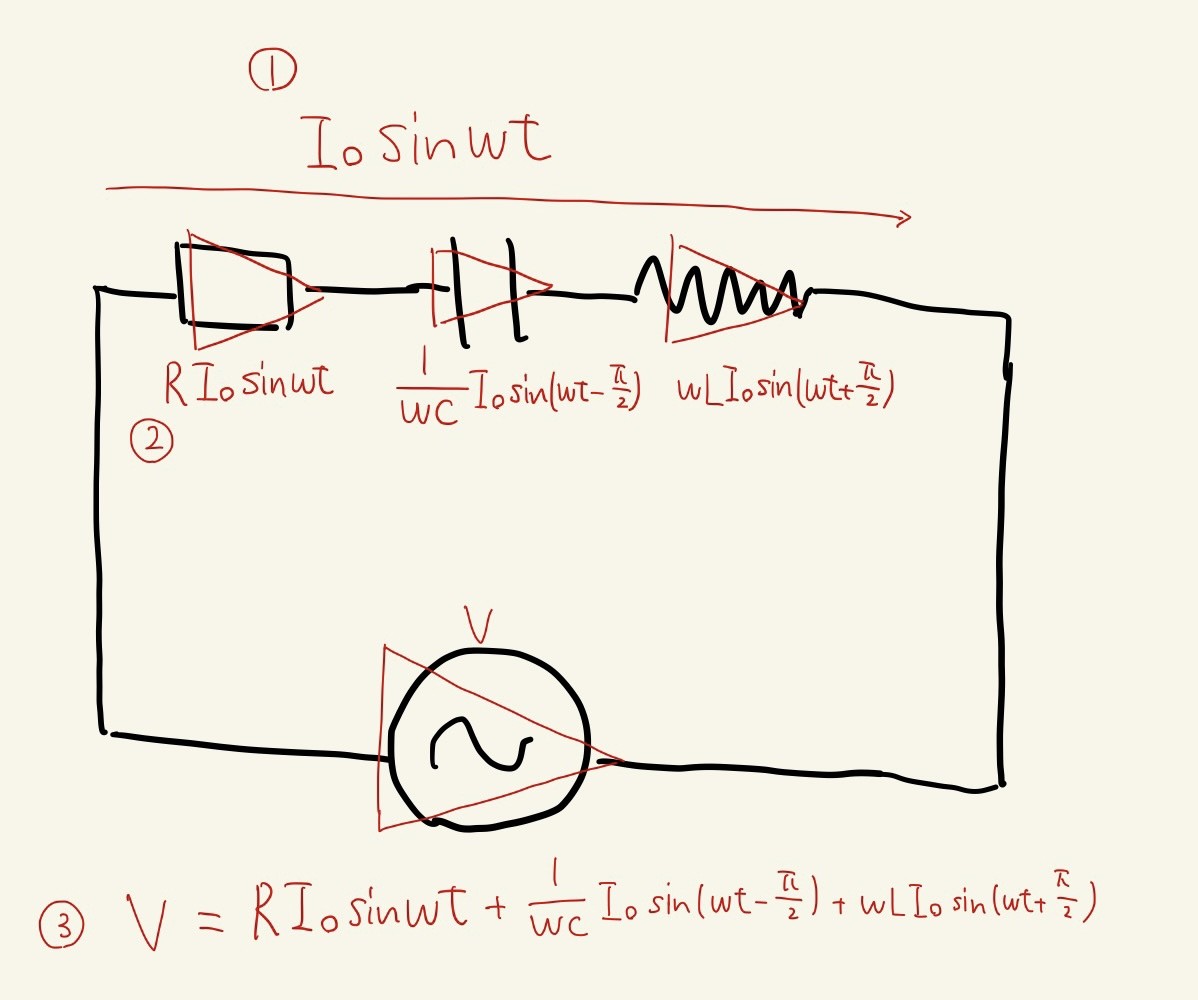
最後に④です。
これはベクトルの足し合わせで考える方法です。図のようなベクトルを書くとy座標の値が足し算を行いたいsinの値と
一致します。つまり3ベクトルを足し合わせてそのy座標の値を考えれば、それが求めたい答えになります。
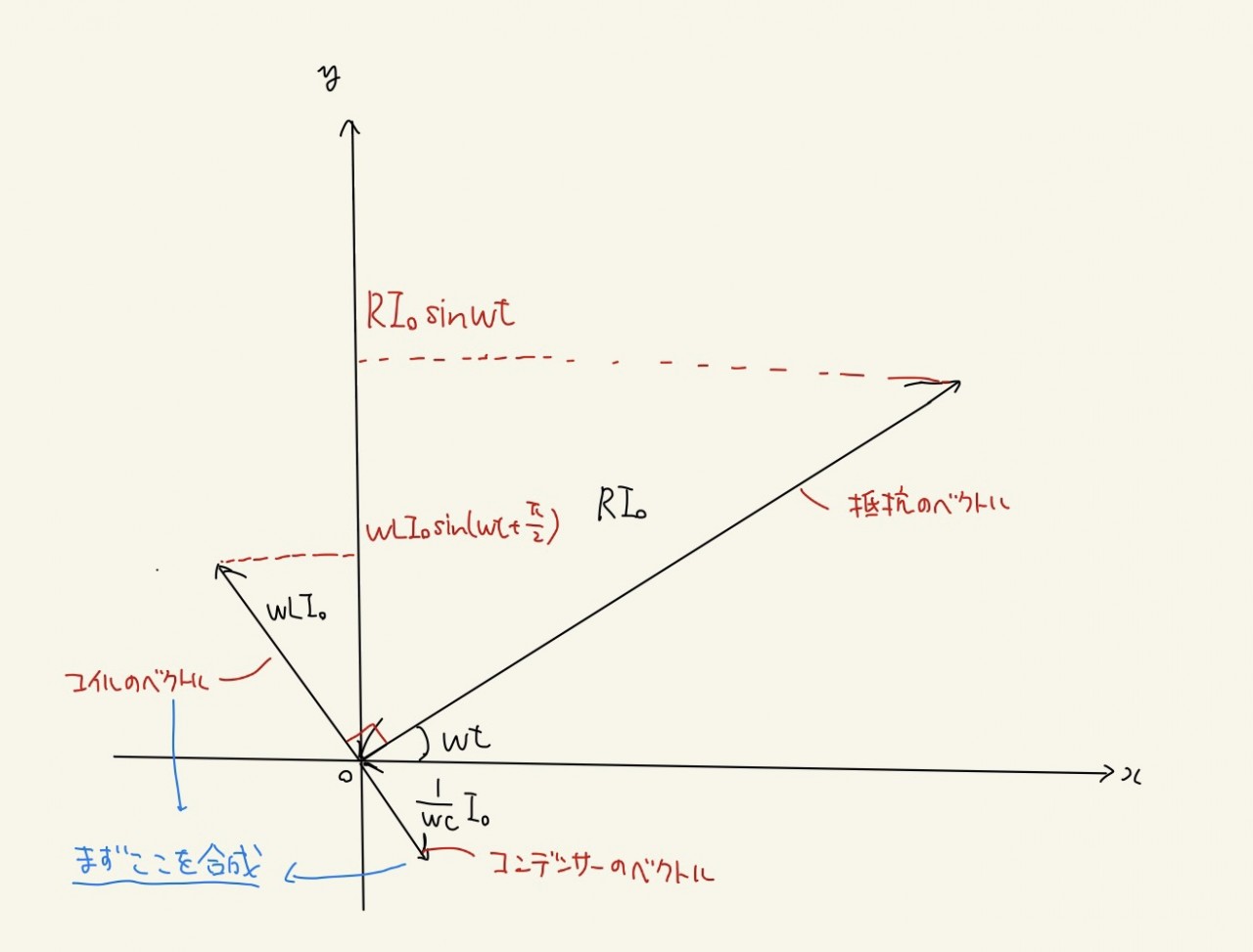
上のような3つのベクトルが書けたら、一組ずつ合成していきます。
コンデンサーとコイルのベクトルが反対方向を向いているので、この二つのベクトルから合成していくと、
簡単にできるでしょう。
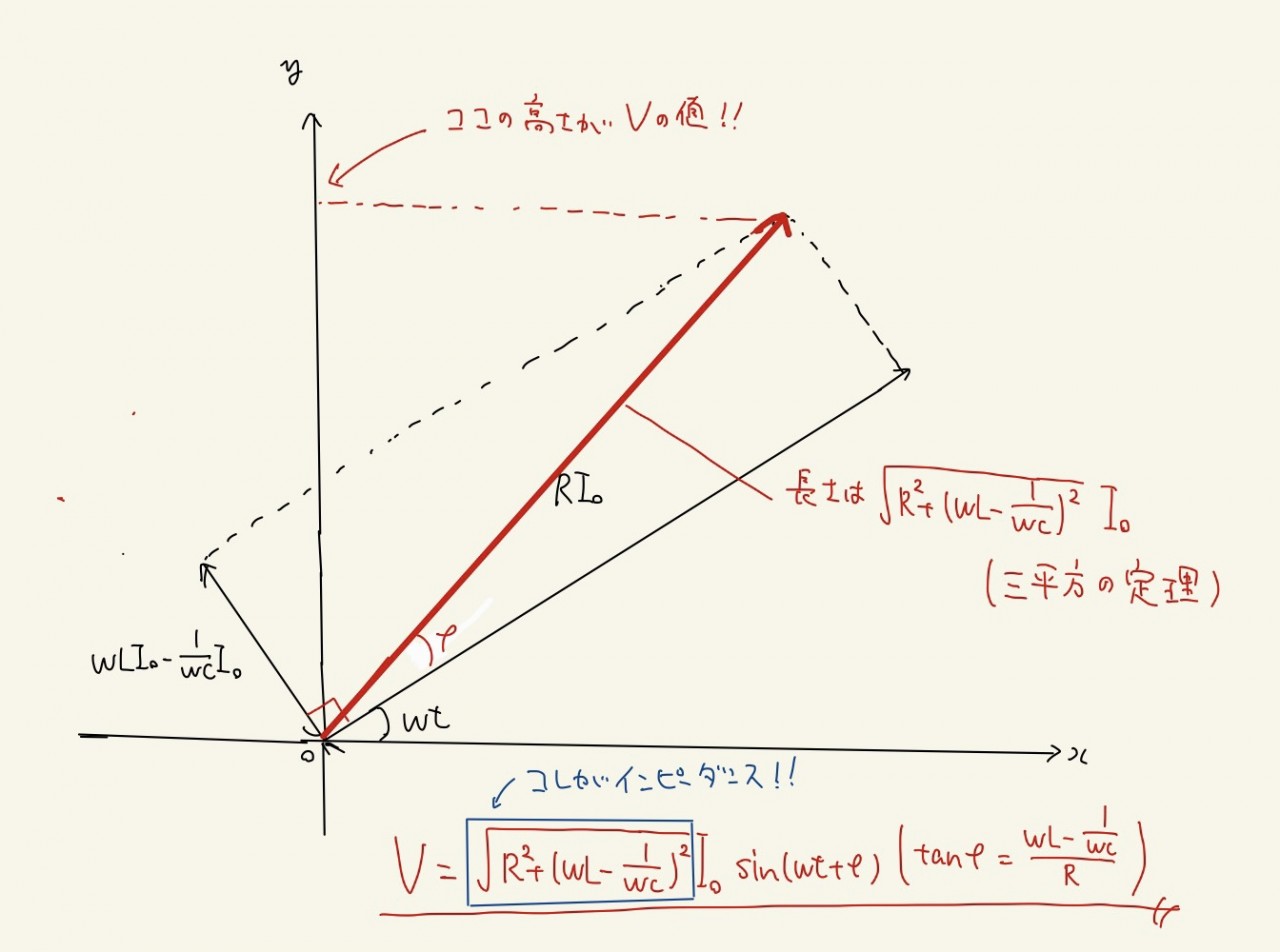
このようにして無事に電源の電圧とインピーダンスを求めることができました。
求めた答えの位相を観察してみると、電源について電圧と電流の位相にはズレが生じます。
このズレはπ/2のように単純なものではありませんが、tanの値については図から求めることができます。
余力のある人は電圧と電流の位相にズレが生じないときのωの値を求めてみましょう。
またそのような状況であるとき、コンデンサーとコイルの電圧がどのように変化しているのか考えてみるといいでしょう。
まとめ
いかがでしたでしょうか?
確かに交流回路は難しい分野ですが、やっていることは普通の直流回路と同じです。
①回路図を書く。
②電流、電圧でおけるものはおく。
③コンデンサー、コイル、抵抗の電圧を求める。
④キルヒホッフの第二法則を立式する。
最後に行った三角関数の合成については物理というより数学的な話なので、ここでは省きました。
交流回路に限らず電磁気の回路問題を解くときにはこの4stepに従って解くことができるように何度も訓練して、おきましょう。
勉強方法、参考書の使い方、点数の上げ方、なんでも教えます ★無料受験相談★受付中★
・模試で思うような結果が出なかった
・他塾のやり方が合わず成績が上がらない
・そもそも受験勉強って何をすればよいのかよくわからない、、、
などなど、受験に対する悩みは大なり小なり誰でも持っているもの。
どんな悩みでもOKです。持ってきてぶつけてください!
受検相談では、、、
- 奇跡の逆転合格プログラム
- 1日で英単語を100個覚える方法
- 志望校合格までのすべて
などなど、100%受験に役立つ情報をお話しします!!
ここまで聞いて、ひとりでできそうなら入塾しなくて構いません!
ぜひ一度ご来校ください!
お申し込みは、下記の無料受験相談フォームにご入力いただくか、
075-606-1381までお気軽にお問合せください!!













