皆さんこんにちは!
今回は、
『誰でも数学で点数が取れるようになる方法』
を伝授したいと思います!
比較的数学のセンスがあると言われ続けてきた私ですが…
『数学のセンス』について熟考し、
やり方一つで『数学のセンス』と
同等の力を手に入れる方法を見つけました。
その方法を忠実に守って勉強してくれた過去の生徒は
『1ヶ月で数学3を完成させた』
『偏差値40から偏差値60まで半年で上がった』
『ずっと偏差値65前後が、70の壁を越えることができた』
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
【『誰でも』やればできる方法】
について、順を追って説明しますが
その方法を『忠実に守る』ことが条件です!
なので、以下の3点を必ず守って読み進めてください!
・読み飛ばさず、納得しながら読む
・この記事の内容を意識しながら数学の勉強をする
・定期的にこの記事に戻って、やり方がズレていないか確認する
では早速!!
今日から「数学のセンス」がある人と同じ…
いや、それ以上の勉強ができるように
『誰でも数学で点数が取れるようになる方法』
を見ていきましょう!!

【広告】==========================
JR「山科」駅から徒歩3分!
京阪「山科」駅から徒歩3分!
京都市営地下鉄東西線「山科」駅 徒歩10秒!
“逆転合格”の「武田塾山科校」です!
山科校は、京都府宇治市、京都市伏見区・南区・中京区・上京区・山科区、長岡京市、向日市、大山崎町、滋賀県大津市など近隣の県からも通塾いただけます。
武田塾には京都大学・大阪大学・神戸大学等の
国公立大学や、早慶上理、関関同立、産近甲龍
といった難関私立大学に逆転合格を目指して
通っている生徒が数多く在籍しています!
=============================
数学が苦手な人ほど、
「数学はセンスだ」
「数学はやってもできない」
なんて思ってしまいますよね。
まず、そんな方に知っておいてほしいことが
『受験数学はセンスではない!』
ということです。
大学受験数学にセンスは必要ない!
まず、皆さんに一つ質問です!
『数学のセンスがある』
って、何をもって
『数学のセンスがある』と判断しますか?

『数学のセンス』とは【 】である!
多くの回答として
「数学の成績がいい」
「発想力がある(問題の解法を思いつく)」
「数学の公式を直ぐ使いこなせるようになる」
などが上がってくると思います。
ところが…
これらは全て結果として見える部分の
『数学のセンス』です。
多くの人が考える『数学のセンス』とは、
結果であって、本質ではないのです!
『数学のセンス』とは【要領の良さ】である!
ここでは『数学のセンス』について
本質的な部分から見直して、
「誰もが数学の問題を解くことができる」方法を伝授します!
数学的視点を明確に持つ
『数学のセンスがある人=要領がいい人』
というのは、
一つの問題を解いた時に
「要点を”無意識”に抑えられている」
という事です。
逆に言えば、数学のセンスがないと思っている人は、
数学のセンスがある人の『視点』を”意識”しながら
勉強しなくてはいけません!
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
「高校数学は演習を積み重ねればできるようになる」
とも、よく言われます。
しかし、”受験”となると時間との勝負になるので
圧倒的な演習量をこなすか、数学の勉強法を正すか。
自分に残された時間も考慮に入れて考えて見てください!
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜

誰でもできる!数学的視点のつけ方
先ほどから出てくる『数学的視点』という言葉…
これは、
「初見問題を解く時に、全く手が動かない!」
という人が欠けている能力の一つとも言えます。
STEP1:公式の覚え方
数学の公式を覚えるときは以下の3点を意識しましょう!
特に、3つ目の(利点)が重要です!!
『いつ使えるのか(条件)』
『式の形(公式)』
『公式の役立ち(利点)』
<例1:三平方の定理>
(条件)直角三角形
(公式)a²+b²=c²
(利点)2辺がわかれば残りの辺もわかる。
逆の定理(公式が成り立つ時は直角三角形)
<例2:底の変換公式>
(条件)log(a)b →対数が与えられている
(公式)log(a)b={log(c)b}/{log(c)a}
(利点)対数の底を合わせることで、計算しやすくなる

STEP2:『操作の流れ』について”目的を基準に”覚える
STEP1では「公式単体の覚え方」についてでしたが
STEP2では、数学的視点の本質とも言える
『操作の流れ』
についてお話ししていきます!
操作の流れとは、
問題文を見てからどの様にアプローチしていくか。
いわば、回答の1行目を書くための流れの事です。
これから説明するやり方を徹底して守り、
まとめた内容を全部覚え切れば、
『数学のセンス』以上の力をつけることができます!
(具体的には、ほとんどの大学の数学入試問題で9割の問題を解くことができます!)
【操作の目的を”細かく”分ける】
数学の理解が難しいと言われる一番の理由が、
『解答の流れ』と『思考の順番』が違う事です。
例えば、直方体の体積を求める問題を見たとき、
解答では3辺の長さを求めるところからスタートします。
本来、体積は(底面積)×(高さ)で求めます。
直方体なら(底面積)=(横)×(縦)で、
結果的に3辺の長さがわかれば体積を求める事ができます。
レベルを上げて、
高校数学の2次関数について見てみましょう。
『aを定数とし、二次関数{y=x²-2ax+3a-2 (0≦x≦1)}の最小値を求めよ』
解答は以下の通り。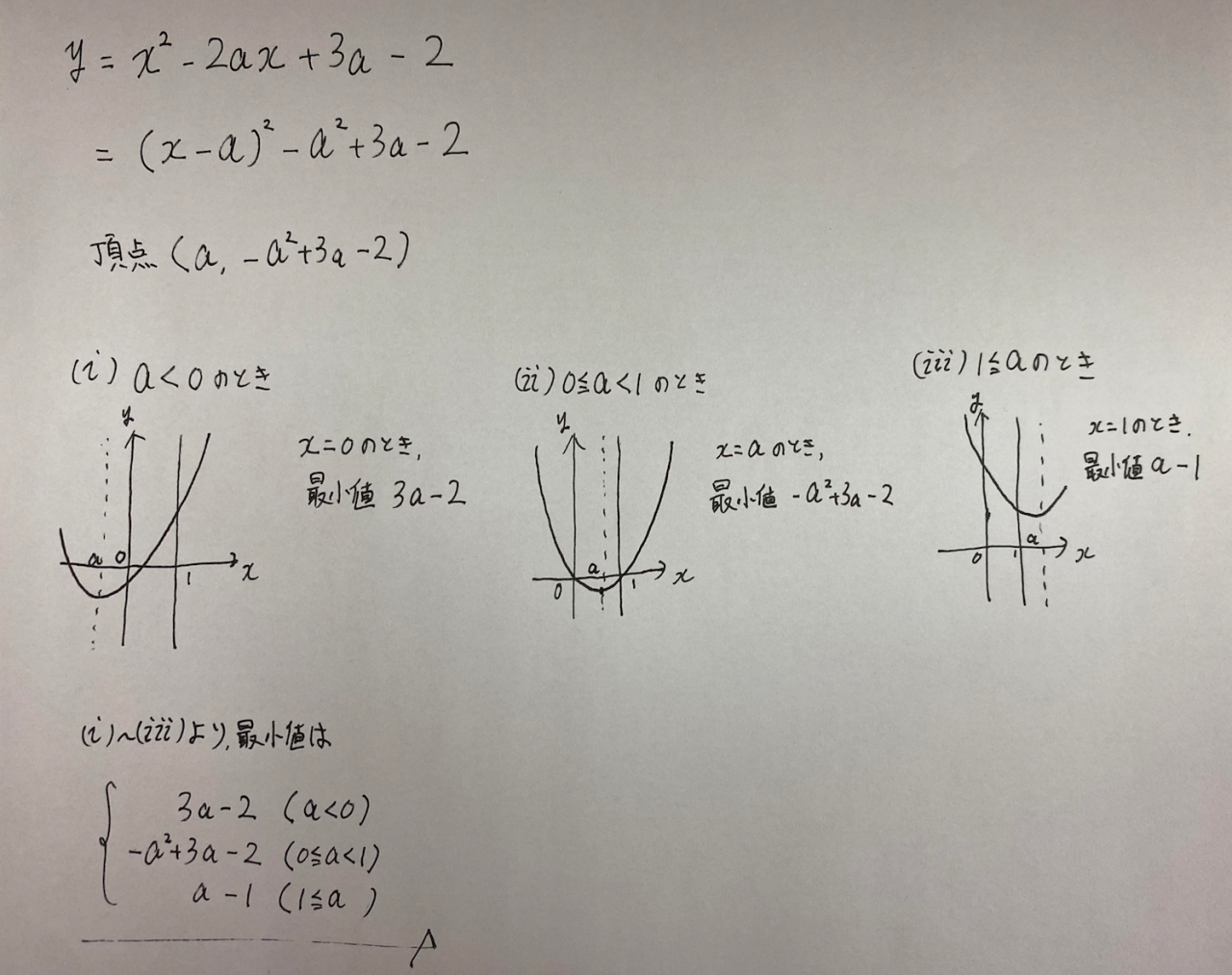
この手の問題は高校数学を学んだ人なら何度も見た事でしょう。
では、この問題を『中学校3年生に教えられますか?』
「まずは平方完成をして〜」
と話したら中学生は「何で??」ってなりますよね…
なので、この問題を解くまでの『操作の流れ』を細かく見て見ましょう!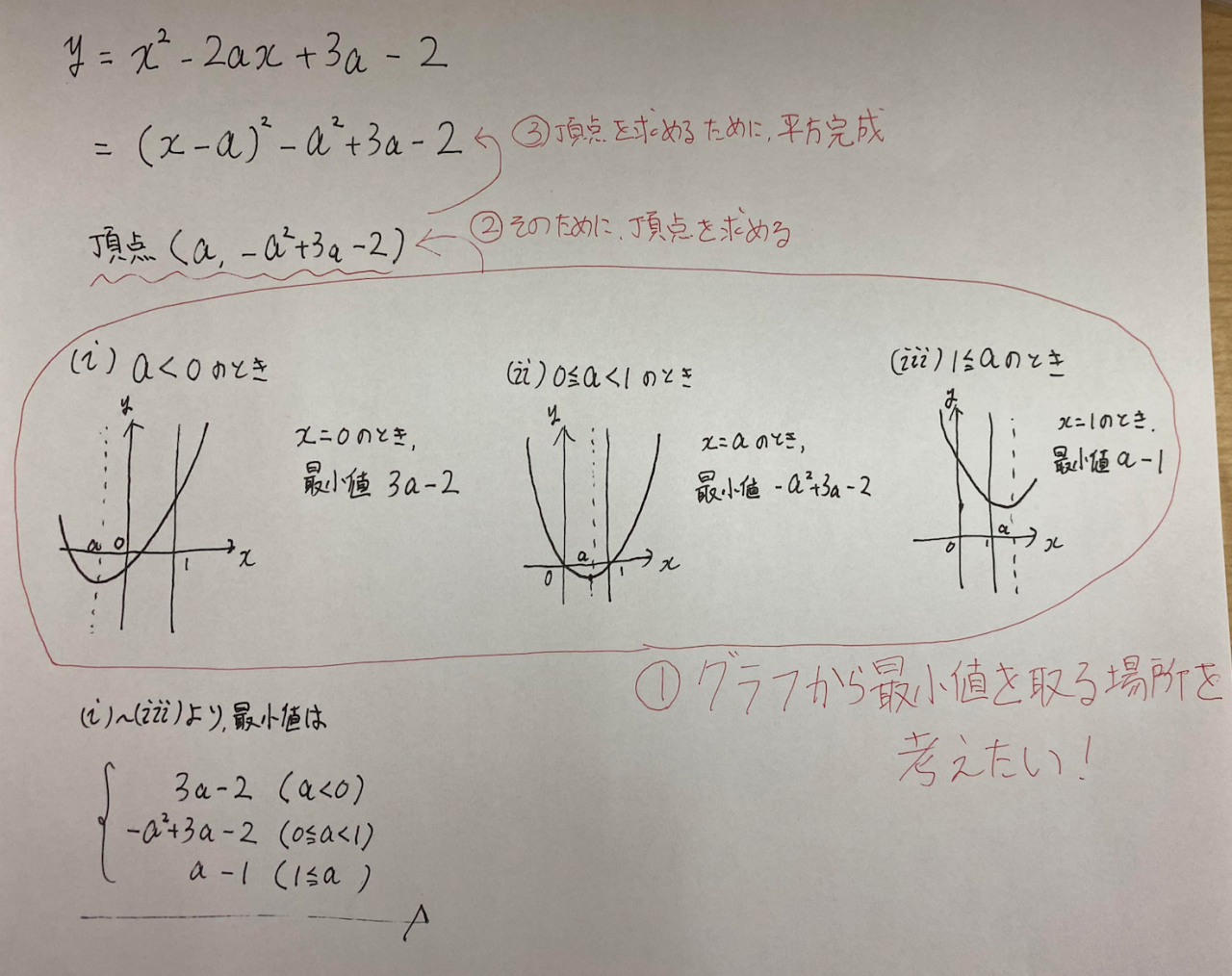
赤で書いたものが、問題を解くまでの「思考の順番」となっています。
二次関数の最大最小問題は『グラフを書く』というのが覚えるべき”知識”であり、
『操作の目的』になります。
①グラフを書きたい
②頂点を知りたい
③平方完成をする
数学では、この様に解を求める為には何が必要か?
という逆算的な考え方が必要なのです。
これを知らずに、何となく演習を積んでいても”数学力”は伸びません!
数学は、どんな教科よりも『目的』が重要
2つのステップに分けた目的は、
『覚えるべき場所を明らかにする為』
・何のために公式を覚えるのか
・何のために式変形をするのか
・何のために図やグラフを書くのか
数学を苦手とする人は皆、
『目的』と『手段』がごちゃ混ぜになっています。
先ほどの問題を再度見て見ましょう↓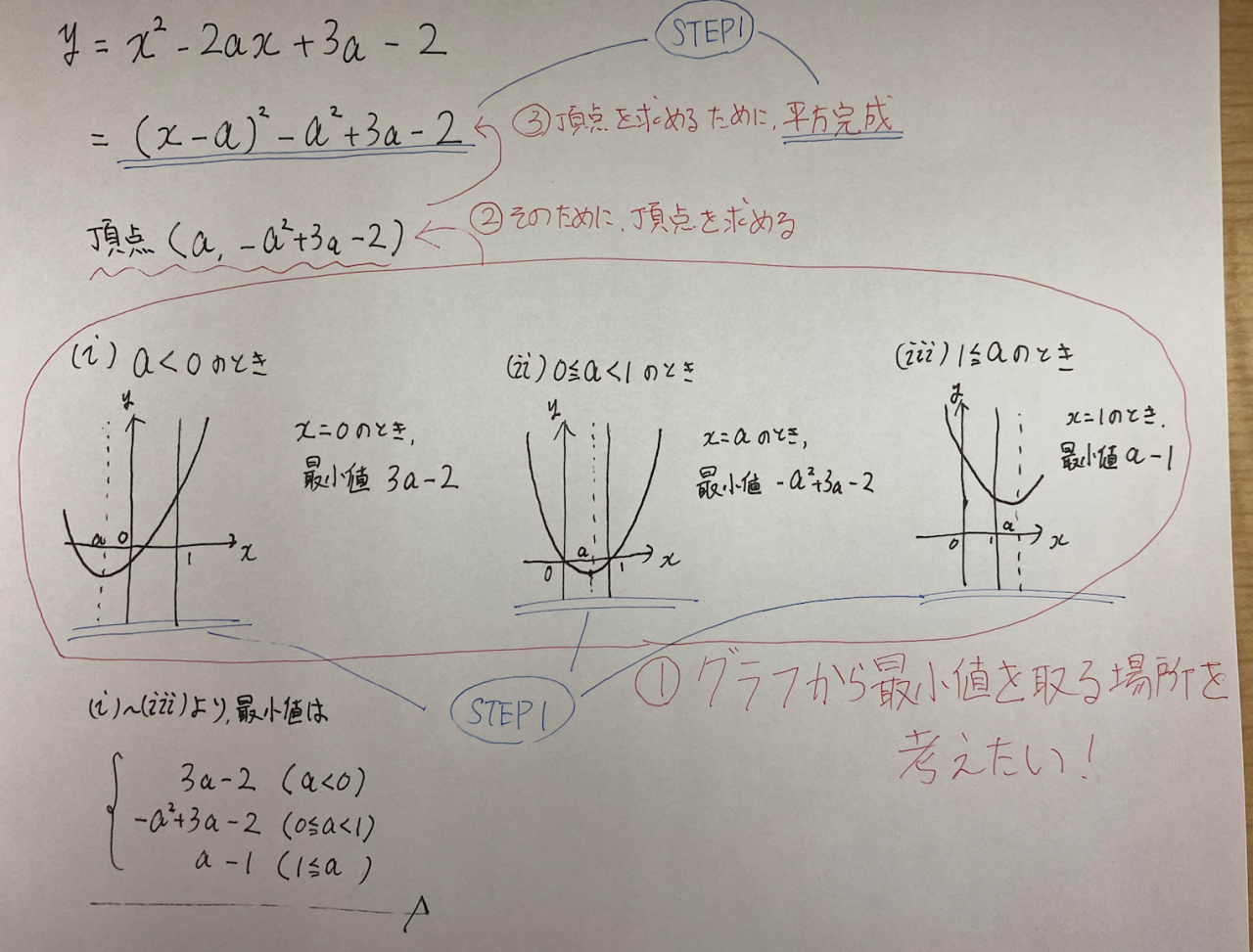
一つの問題の中でも、
『STEP1の覚えるべき公式』と
『STEP2の操作の流れ』
が入っています。
何度も言いますが、
数学は『目的』が一番大事です!!
一つの問題に対して、流れを覚えるのではなく、
『なぜその様な流れになるのか』
を覚える様にしましょう!
【要注意!】”理解する”という言葉は罠
よく聞く、数学の勉強法として
『公式を根本から理解しよう!』
というものがありますが、
はっきり言って「数学的視点」を持っていない人が
公式について深掘りしても無意味です!!!
『公式を根本から理解すれば良い!』
という人は総じて元から「数学的視点」がある人です。
そんな人のアドバイスを聞いても毒にしかならないので気をつけましょう!
(そもそも、根本から公式を理解ってなんやねんって感じですよね!)
数学の成績に直結する勉強法
これまで「数学のセンス」について深掘りし、
『数学的視点』の付け方を話してきました。
ここでは、具体的な数学の勉強法について深掘りしていきます!
2パターンに分けて説明します!
①これから数学の勉強をする人
②数学の偏差値が伸び悩んでいる人
(偏差値別の内容については後ほど…)
①これから数学の勉強をする人
『数学的視点の付け方』を意識しながら進めて欲しいですが、
まずは一通りどの様な解法があるのか知るところから始めましょう!
解答解説を読んで理解できる様になる事が優先となります。
具体的なやるべき内容は後述の
『【偏差値別】数学の勉強内容』
を参考にしてください!
②数学の偏差値が伸び悩んでいる人
一通り学習を終えたが初見問題が取れず、
数学の偏差値が伸びないという人に向けて。
この様な現象に陥っている人の多くは
「解説を見れば理解できる」
「ただ思いつかなかった」
「(独自のやり方で)ケアレスミスをした」
という事が多いと思います。
これらは全て『数学的視点』が
抑えられていない事が原因となっています。
特に「解説を読めば理解できる」というのは、
知識自体は持っていたけど『使えなかった』
という事なのです。
やる事は最初に話した『数学的視点の付け方』を徹底する事ですが…
イチからやり直すのも大変ですよね…
なので最短最速かつ、
実戦形式の中で『数学的視点』を修正する方法を教えます!
数学の実戦形式勉強法
まずは、
「考えたけど思いつかないから何も書かなかった」
という状況を無くすことから始めましょう。
【考えたことをノートに残す】
問題を解く事に意識がいきすぎて、
答えにたどり着くまでの道筋が思いつかなかったら
白紙のまま解答解説を読み出す人がほとんどだと思います。
この勉強の仕方は、数学の勉強を始める人がやるもので、
一通り学習を終えた人はこのやり方からいち早く脱却しなければなりません。
問題を見て
「何を思ったのか」
「何が嫌なのか」
「何の知識を使おう」
それぞれ思ったことをノートに残し、
「これ以上考えられない!」
「問題を解く事ができない!」
と、なってから
解答解説を見ます。
自分が書き出した物で解けるのであれば、
その知識について『数学的視点』を掘り下げ。
書き出したものでない解き方であれば、
同じくその知識について『数学的視点』をまとめ、覚える。
<Point:解き直しの仕方>
ただ問題を解き直して正解するだけでは甘いです!!
その問題を見たときに
「どんな事が考えられ」
「正解へのアプローチ」
を人に説明できるかどうかを確認しましょう!
ただ正解できるだけでは今後、
同じ”考え方の間違い”を犯してしまうからです。
【偏差値別】数学の勉強内容・オススメ参考書
数学の偏差値をあげるのに一番大事なのは
『何から勉強するか』です!
現状の偏差値別に
『何をすべきか』
まとめるので、自分の現状を把握し
数学の偏差値を上げるための勉強を
今日から始めましょう!!
数学偏差値〜44
数学の偏差値が45以下の方は
『主流問題の基礎』を徹底することから始めましょう!
ここでいう『主流問題』とは、
数学の勉強で最初に抑えるべき問題を指します。
以下に挙げる内容について
『一通り説明できる』
ようになることが、
数学の成績を伸ばすための第一歩になります!
では、具体的な内容について見てみましょう!

数学の最初に抑えるべき内容
【数学1・A】
(数と式)数の表し方・式変形のルール
(2次関数)グラフの書き方・最大最小値
(図形と計量)三角比の定義・三角方程式・正弦余弦定理
(整数)倍数約数・不定方程式・n進法
(場合の数)樹形図・順列と組み合わせ
(確率)定義式・足すかかけるか・余事象
【数学2・B】
(式と証明)比例式・恒等式
(複素数と方程式)複素数の定義・因数定理
(図形と式)点と直線の距離・円の方程式
(三角関数)加法定理・三角方程式
(指数対数)指数対数の定義・方程式・不等式
(微分積分)微分積分の意味と計算・接線の方程式
(数列)等差等比数列・シグマ・漸化式の操作
(ベクトル)内積・ベクトル方程式
【数学3】
(式と曲線)曲線の定義式・曲方程式
(複素数平面)複素数計算・ドモアブル
(極限)不定形の式計算・極限公式
(微分法)微分の定義・計算方法
(微分法の応用)接線の引き方
(積分)基本積分・置換積分・部分積分
オススメ参考書
【数学 入門問題精講】
この参考書は、主流問題に的をしぼって細かい解説までしてくれている、
問題集かつ教科書的な参考書になっています。
この参考書に乗ってあることを一通り知っておければ、
次の参考書の解答解説も理解しやすくなります。
数学偏差値45〜54
数学偏差値45を超えても、
なかなか55を超えることができない…
数学偏差値が50前後で止まっている人の原因は
先述の『数学の最初に抑えるべき内容』のなかで、
何となく理解した”つもり”で終わらせている単元がある
ことです。
『数学の成績に直結する勉強法』の
『②数学の偏差値が伸び悩んでいる人』
の勉強法を、主流問題に的を絞って取り組みましょう!
オススメ参考書
【数学 入門問題精講】
※『数学偏差値〜44』のオススメ参考書に記載。
この参考書の中で漏れがないか今一度確認を!
【数学 基礎問題精講】
この参考書は、標準的な入試問題を集めた問題集で、
ここに乗ってある知識を全て活用できる様にすれば、
入試問題で9割の得点を狙う事ができます。
→(参考)【実証】武田塾の数学ルートで合格点が取れるのか⁉︎基礎問題精講で足りる?
(基礎問題精講だけで入試問題を解いた内容が書いてあります!)
この偏差値帯の人であれば、一通り基礎問題精講をやって見て
わかりづらい部分を【入門問題精講】で復習しましょう。
数学偏差値55〜59
数学偏差値55は超えるが、安定して60以上がでない…
そんな人の多くの原因は『苦手単元』が存在する事です。
主流問題を抑えられれば偏差値55は到達しますが、
その先はちょっとした応用を効かせた問題を取れる様にならなければなりません。
(※応用といっても、基礎知識の組み合わせです)
ここの偏差値帯にいる人にやってもらいたい事は
『単元を絞った勉強』をする事です。
オススメ参考書
【基礎問題精講】
※『数学偏差値46〜55』のオススメ参考書に記載。
知識的には基礎問題精講で十分。
解けなかった問題は全てこの参考書
のどこに書いてあったかを確認する様に!
【センター過去問】
「え⁉︎センター試験?」
と、思う方も多いと思います。
今年から共通テストに変わりますが、
ここでのセンター過去問は”目的”が違います。
センター試験は基本的な内容を満遍なく出題してくれています。
自分がどの単元が苦手なのかを見つけるために、
センター過去問はとてもいい教材として使えます!
安定して75%以上を取れる様に、
過去問演習→基礎問題精講対応→過去問演習…
を繰り返していきましょう!!
数学偏差値60〜69
さて、かなりレベルが上がってきましたが…
ここで一旦確認です!!
今まで数学偏差値別にオススメ参考書を上げてきましたが、
ただやればいいというものではありません!
あくまでその偏差値帯にいる場合のオススメであって、
偏差値が超えていても基礎は重要です。
『数学的視点』に書いてある勉強がちゃんと意識できているか、
今一度確認しましょう!!

では、数学偏差値60〜69の方へ向けた話をしていきます。
偏差値70を超えるためには、
基礎問題精講の知識はわかっているのを前提に、
単元を超えた知識のつながりが必要となります。
例えば『確率漸化式』の様な、
『確率』と『漸化式』を組み合わせた標準問題。
『確率漸化式』はどんな参考書でも取り上げられる問題ですが、
『整数+2次関数』の様に、初見ではなかなか手をつけづらい問題が入試では頻出です。
こういった問題に対して、
”素早く”解法を導けるかどうか判断する力が必要になります。
(捨て問判断)
この力の付け方は『数学的視点』を増やすことになります。
たくさんの問題に触れ、
自分になかった知識のつながりについて
『なぜ思いつかなかったのか』
『どうすれば思いついたのか』
を考え、覚えましょう!
オススメ参考書
<理系>
【理系数学入試の核心 標準編】
理系数学の入試問題150問を集めたものです。
定石問題が多く収録されているため、
この参考書”だけ”を使いこなすことで、
私立理系大学に合格する人が多い参考書の一つです。
基礎問題精講を使ってきている人は、
必ず基礎問題精講をベースにこの参考書を使いましょう!
<文系>
【文系の数学 実践力向上編】
この参考書は『文系の数学 重要事項習得編』の上位参考書になります。
基礎問題精講と重要事項習得編は同レベルとも言えます。
こちらの参考書は、
理系でも頭を悩ます様な単元を超えた問題が多く収録されており、
より発展的な問題を網羅しています。
<文理両方>
【数学 重要問題集(A,B)】
難関大学を目指す人なら聞いたことがあるであろう『重要問題集』
私立や国立入試で見られる”嫌な出題形式”に慣れることができます。
難しい問題文に慣れていない人は是非取り組んでもらいたい問題集です。
数学偏差値70〜
数学偏差値70overとなると、
偏差値を上げるというよりも
”精度”を上げることが重要になります!
東京一工(東京・京都・一橋・東工)を目指すのであれば、
15カ年分の数学を用意し、
それぞれの問題について研究することをオススメします。
特に、整数問題などは徹底的に詰めないと
手がつかない問題が多いです。
医学科を目指す人は、
少しのミスも許されないので、
基本的な問題を早く正確に解く練習をしましょう。
オススメ参考書
【数学 青チャート】
みんな大好き青チャート。
偏差値70overだからこそ全ての問題を解くのではなく、
苦手意識のある単元や、解くスピードの遅い単元を絞って
点数を安定させる目的で使いましょう。
【プラチカ】
難関大学を目指すならやっておきたい!
この問題集を使うのは”基礎”が固まっているのが前提。
初見でどこまで解けるか腕試しをしつつ、
新しい考え方などを次に活かせる様な覚え方をしましょう。
【過去問】
問題集は大学入試問題の過去問から抜粋した良問揃いなのが
良い点であり、悪い点でもあります。
限られた時間内で、目標点を取るための『戦略立て』
こそが、最後の合否を分ける力となります。
時間に余裕がある人は様々な大学の過去問にチャレンジして見ましょう!
さいごに
ここまで読んでくれて、
ありがとうございます!
多くの人が当てはまる内容についてまとめてみました。
この記事を読んで後に、実行に移してくれれば
以前よりも数学に対して前向きに取り組める様になるでしょう。
残念ながら、ここに全ての知識を書くには余白が狭すぎる…(ある数学者の真似)
一人一人、やるべき内容や勉強の仕方が変わってくるのも数学。
自分一人では難しいと思う方や、
数学に不安が残る人は是非ご相談ください!
また、様々な数学の記事も用意したので、
よかったらのぞいてみてください!!
武田塾の数学ルートは本当にいいのか?
【実証】武田塾の数学ルートで合格点が取れるのか⁉︎基礎問題精講で足りる?
大学入試問題の分析
【2020年阪大入試】大阪大学理系数学を分析|各問題の着目点
【2020年京大入試】京都大学理系数学を分析|各問題の着目点
2020大阪府立大学 理系数学 入試問題の難易度を評価・分析!合格点や対策を考察!
2020神戸大学 理系数学 入試問題の難易度を評価・分析!合格点や対策を考察!
2020京都工芸繊維大学 数学 入試問題の難易度を評価・分析!合格点や対策を考察!
勉強方法、参考書の使い方、点数の上げ方、なんでも教えます ★無料受験相談★受付中★
・模試で思うような結果が出なかった
・他塾のやり方が合わず成績が上がらない
・そもそも受験勉強って何をすればよいのかよくわからない、、、
などなど、受験に対する悩みは大なり小なり誰でも持っているもの。
どんな悩みでもOKです。持ってきてぶつけてください!
受検相談では、、、
- 奇跡の逆転合格プログラム
- 1日で英単語を100個覚える方法
- 志望校合格までのすべて
などなど、100%受験に役立つ情報をお話しします!!
ここまで聞いて、ひとりでできそうなら入塾しなくて構いません!
ぜひ一度ご来校ください!
お申し込みは、下記の無料受験相談フォームにご入力いただくか、
075-606-1381までお気軽にお問合せください!!















