数学で「分数が苦手」という方は多いのではないでしょうか。
分母と分子、両方に偶数が入っていれば
「少なくとも2で約分できる」ということが分かります。
しかし、「分母と分子に少なくとも1つ、奇数が混じっている場合」に
正答率が大幅に落ちる傾向にあります。
もっとも、2で約分を続けていって
「分母と分子に少なくとも1つ、奇数が現れた」場合、
そこでまだまだ約分できるにも関わらず約分をやめてしまい、
結局「不正解」という方もいます。
いきなりですが、問題です。
(問)次の①~⑥を約分せよ。
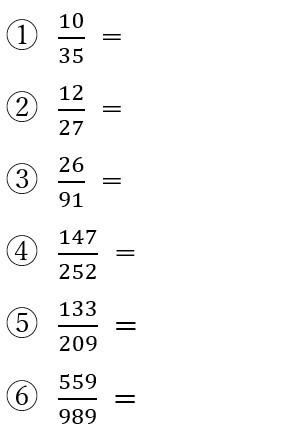

約分は、3パターンの解法を押さえよ!
九九レベルの約分は、「2, 3, 5の倍数」
上の(問)の①と②は、まず2, 3, 5の倍数で約分できるかどうかを考えます。
(こちらは小学生レベルの問題になります)
このうち、2, 5の倍数の性質は比較的答えやすいのではないかと思います。
◆2の倍数=偶数
◆5の倍数=下1桁が5または0で終わる数
しかし、3の倍数の性質は?と聞かれたとき、すぐに説明できますか?
◆3の倍数=各桁の和が3の倍数
実は、約分の時に「3で割れるかどうか」を見落とす人が結構います…。
例えば、4桁の自然数「3507」があったとします。
これは3の倍数でしょうか?
3の倍数かどうかを確かめるために、各桁の数字を1つずつ足し算していきます。
3507:3+5+0+7=15
15は3の倍数なので、3507は3の倍数ということが出来ます。
え、なんで?となっている方へ、簡単に証明を載せておきます。

もちろん、何桁の整数でも同様に証明することが可能です。
これで、①と②は間違えることなく約分が可能となります。
(④でも3の倍数の性質を利用します)
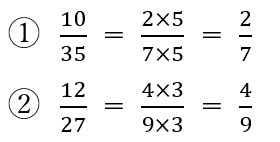
素因数分解を用いる
まず、質問です。
素因数分解とは何か、説明できますか?
素因数分解とは、ある正の整数を「素数の積の形で表すこと」です。
では、素数とはどのような数なのでしょうか?
答えは「1と自分自身(の数)以外に約数を持たない正の整数」です。
少し話が脱線しますが、
数学は他教科と違って用語を答えさせる問題が出ないので、
用語の意味を軽視しがちです。
しかし、用語の意味をしっかり説明できる状態にしておかなければ
何を求めればよいのかが分からなくなってしまいます…。
話を戻しましょう。
100までの素数は25個あります。
(2は偶数で唯一の素数です。1は約数が1だけなので素数ではありません)
これくらいであれば、覚えておいた方が得ですね♪
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 83, 89, 97
では、63を素因数分解してみましょう。
63は3の倍数なので
63 = 3 × 21
21も3の倍数なので
63 = 3 × 3 × 7 と表すことが出来ます。
次に、奇数の約数を見つけるコツですが、
・3, 5のいずれの倍数でもなければ7の倍数を疑う。
・それ以外では、11以降の素数で割れないか試す。
上記2つを試してみてください!
例えば、③の場合。
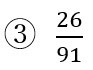
まず26を素因数分解し、
26=2×13 の状態にします。
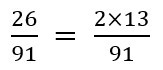
ここで、91に注目します。
一見91は素数っぽく見えますが、91を13で割ってみましょう。
91=7×13 となり、7と13を約数に持つことが分かります。
よって、③は以下の通り約分することが出来ます。
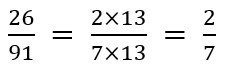
④の場合はどうでしょうか。
まず、147を素因数分解しましょう。
147の各位の数を足し算すると、1+4+7=12となり、
3の倍数だということが分かります。
147=3×49=3×7×7 となります。
252についても3の倍数なので
252=3×84 となります。
ここで、84が7の倍数かどうか調べます。
これは、147の約数である49が7でしか割ることが出来ないためです。
84=7×12となり、84は7の倍数であることが分かります。
したがって、約分は次の通りに行うことが出来ます。
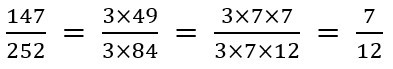
素数同士の積になっていないか?
⑤と⑥はかなり厄介です。
まずは⑤から見ていきましょう。
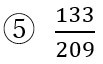
この場合は、分母と分子のうち「小さいほうの数」を選びます。
11×11<133<12×12より、
{3, 5, 7, 11}の素数で割り切れないかどうか確認する作業を行います。
3と5では割れませんが、7だと割り切れます。
133=7×19
次に、209を7, 19で割り切れるかどうか確かめます。
7では割れませんが、19だと割り切れます。
209=11×19
したがって、⑤は以下の通り約分が出来ます。
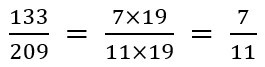
これと同じ要領で⑥も解けます。
一度、みなさん自身で試してみてください!
(⑥の解答)
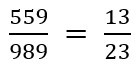
武田塾八事いりなか校からご挨拶
みなさん、こんにちは!
学力・偏差値を上げる【正しい勉強方法】を教える予備校・個別指導塾の
武田塾八事いりなか校です\(^o^)/
武田塾八事いりなか校は、名古屋市営地下鉄:八事駅6番出口から
徒歩1分の予備校・個別指導塾となります!
武田塾八事いりなか校は
「学力を大幅に上げる正しい勉強法を教える塾」です!
近隣の高校(南山女子・南山男子・中京大中京
・名古屋高校・名大附・東海学園・天白高校
・金城学院・愛知高校・日進西高校・愛工大名電など)や、
名古屋市(特に千種区・名東区・天白区・瑞穂区・昭和区)、
日進市の学生さんを応援しています!
日々の勉強はどうやっていけばいいんだろう…
志望校に合格したい、だけど受験勉強が不安という方は、
ぜひ武田塾八事いりなか校の無料受験相談までお越しください。
(実は、ここでお伝えする勉強法は大学入試だけでなく、一生使える勉強法なんです…!)
下の黄色いボタンから
フォームを入力してもらえば、すぐに予約が取れます。

※お電話で日程を調整させていただきます。
人気のためすぐに予約枠が埋まってしまうので、
お早めにご予約よろしくお願いします。










