令和5年大学入試共通テストを解説します - 数学Ｉ・A

こんにちは！武田塾つくば校です。

令和5年大学入試共通テストの解説をします。
今回は数学I・Aです。

第１問（必答問題）

〔１〕数と式（絶対値、不等式、有理化、式の展開）

まず、絶対値は見た瞬間に外すようにすること。絶対値記号がついたままでは計算できません。
公式としては

｜ｘ｜＝ａ⇒ｘ＝ａ（ａ≧０）、ｘ＝ーａ（ａ＜０）

｜ｘ｜＞ａ（ａ＞０）⇒ｘ＜ーａまたはｘ＞ａ

｜ｘ｜＜ａ（ａ＞０）⇒ーａ＜ｘ＜ａ

といったところ。

次の分母の有理化は不等号が絡んでいるので、負の数を掛けたり負の数で割ったりしたときに向きが変わることに注意。
絶対値を外して整理したときに

ー８≦(１－√３)(ａ－ｂ)(ｃ－ｄ)≦ー２

となるので、ここですべての辺に「ー」を掛けておいて

２≦(√３ー１)(ａ－ｂ)(ｃ－ｄ)≦８

としておくのも一つの手（問題の注意は無視することになるけど）。こうしておけば扱うのは正の数だけになるのでいろいろ気を使わなくて済むようになる。

そのまま「１－√３」で割った場合は不等号の向きやわらわら出てくる「ー」に注意して計算を進める。

最後の問題はノーヒントならどうしようかとすこーし考えてしまいそうだけど、問題文に「左辺を展開」せよとの指示が出ているので、これに従って展開していけばいい。
そうすると

①：ａｃ－ａｄ－ｂｃ＋ａｄ＝４＋４√３
②：ａｂ－ａｄ－ｂｃ＋ｃｄ＝－３＋√３
③：ａｃ－ａｂ－ｃｄ＋ｂｄ＝？

①と②でピンク背景部分が共通しているので、「①の左辺ー②の左辺＝③の左辺」になることに気づければＯＫ。

〔２〕図形と計量（正弦定理・余弦定理、三角形への応用）

（１）

基礎的な問題だが、（ii）では△ＡＢＣの面積が最大になるのは点Ｃから辺ＡＢに下した垂線が円の中心Ｏを通るとき、とすぐわかるようになっておこう。

△ＡＢＣの面積Ｓは「Ｓ＝(１／２)ａｂsin∠ＡＣＢ」よりは底辺と高さから求めたほうが簡単。

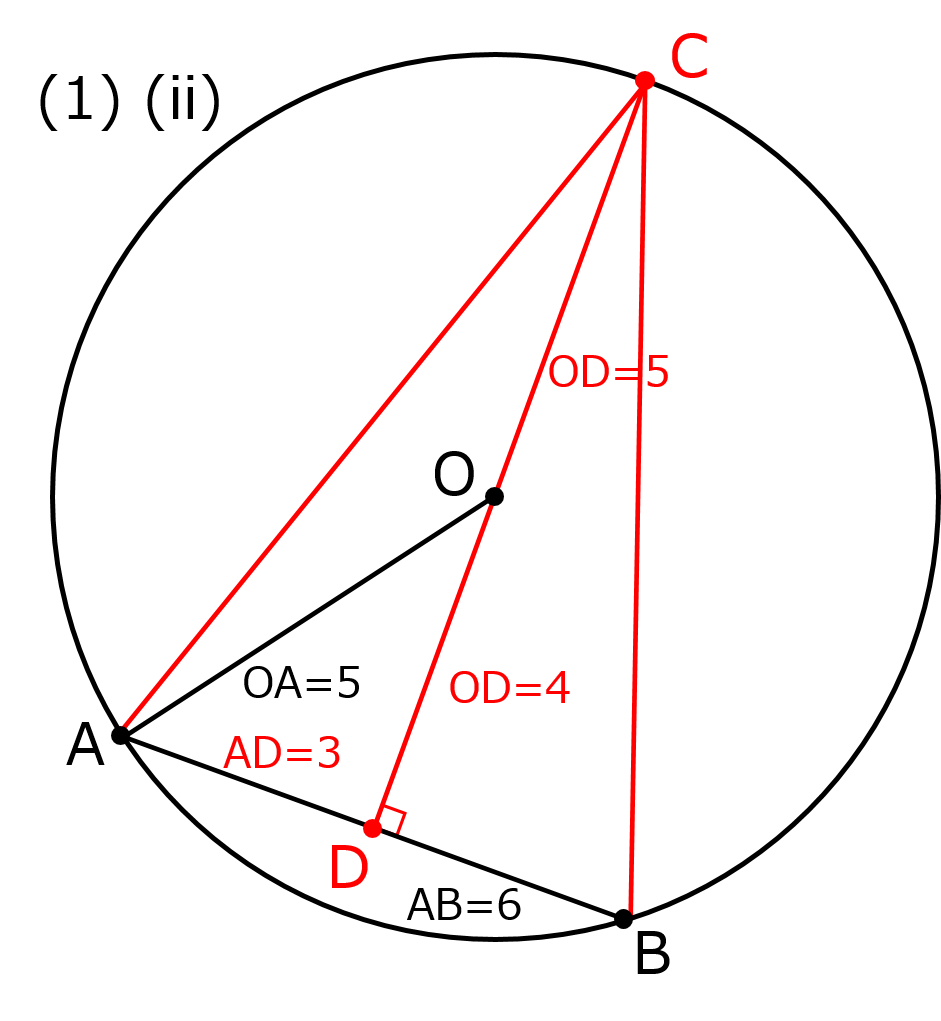
第1問〔2〕(1)(ii)

（２）

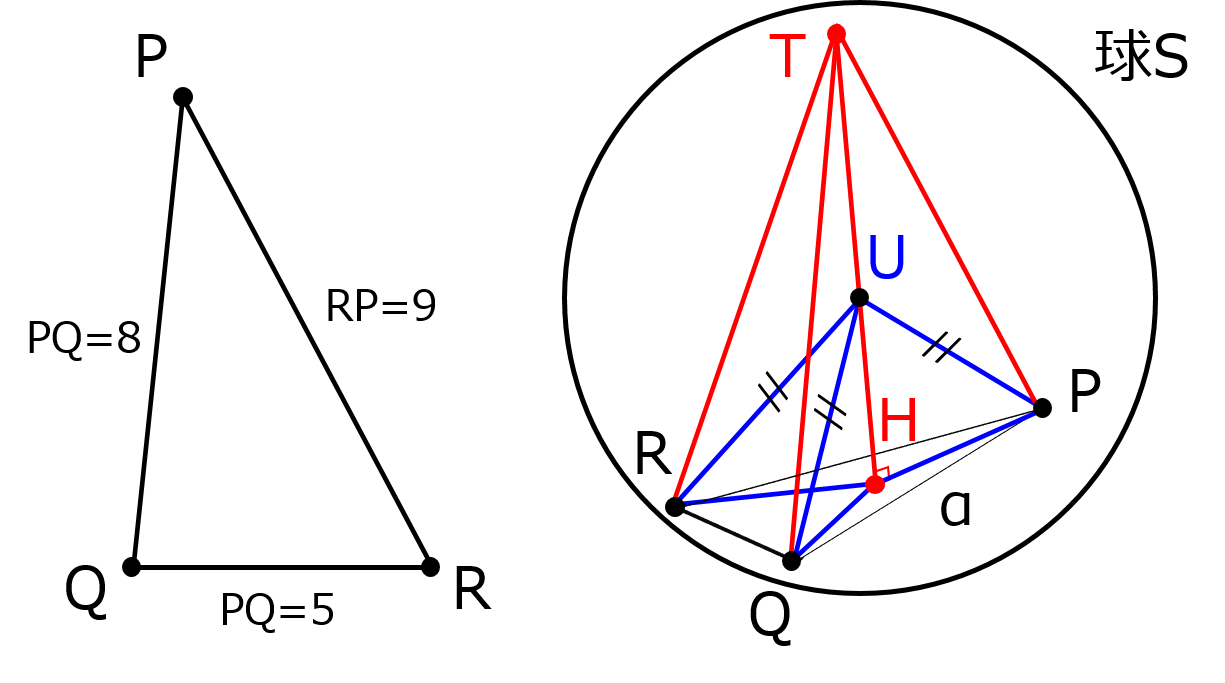
今度の△ＰＱＲの面積は上の公式から求める。

三角錐ＴＰＱＲの体積が最大になるときだけど、（１）と似ていてＴから面ＰＱＲに下した垂線が球Ｓの中心を通るときとなる。

それが分かれば△ＯＰＨ、△ＯＱＨ、△ＯＲＨにおいて、
ＯＰ＝ＯＱ＝ＯＲ（球の半径）、ＯＨは共通、∠ＯＨＰ＝∠ＯＨＱ＝∠ＯＨＲ＝９０°より
△ＯＰＨ≡△ＯＱＨ≡△ＯＲＨ（直角三角形の斜辺と他の一辺がそれぞれ等しい）となるので、
⑥ＰＨ＝ＱＨ＝ＲＨが選べる。

三角錐ＴＰＱＲの体積については、底面積（△ＰＱＲの面積）はすでに出ているので、高さ、しかもＴＨのうちＯＴはやはり球の半径でわかるので実質的にはＯＨの長さを求めるだけ。

第1問〔2〕(2)

第２問（必答問題）

〔１〕データの分析（ヒストグラムと四分位数、箱ひげ図、分散、共分散）

分散や共分散・相関係数、四分位数、箱ひげ図の内容などはまぁ常識にしておく。今回の問題では、これだけで２問は確実に解ける。

（１）

ヒストグラムに度数の累積を書き込むなりして第１四分位数、第３四分位数がどの階級に含まれるかを確認。

四分位範囲は「第３四分位数ー第１四分位数」なのだが、今回は具体的な数値はわからないので、取りうる値で考えることになる。具体的には

「第３四分位数の階級の最小値ー第１四分位数の階級の最大値」より大きく「第３四分位数の階級の最大値ー第１四分位数の階級の最小値」より小さい

となる。

（２）

（i）第１四分位数、第２四分位数（中央値）、第３四分位数は、要するにそれより小さい値がそれぞれ全体の１／４、１／２、３／４あるという目印。地域Ｅでは中央値が２６００より小さいので２６００未満の市は５割以上あるのに対して、地域Ｗでは中央値が（ぎりぎり）２６００より大きいので５割未満であることを意味する。

（ii）ただ分散の定義を聞いているだけ。

（３）

これも相関係数の定義が分かっていれば、表１から必要な数字だけピックアップして計算するだけである。最後は筆算すると思うけど、「０．３」が出た時点で選択肢は一つに絞れるので、それ以上計算する必要はない（時間のムダ）。

〔２〕２次関数（身の回りへの応用）

数学の試験なのにやたら文章が長くて、はじめは「何の話してるんだ？」となるかもしれないが、よくよく考えてみればただの２次関数、という問題。これにいかに早く気づけるかが大事である。
問題演習ならなんてことなくても、試験の独特の雰囲気にのまれてテンパることは十分ありうるので、普段から模試を受けるなりして場慣れしておこう。

（１）

Ｃ１もＣ２も２点しかわからないので、ａやｐは消えずに残ることになる。今回の事例においてはどのくらいの高さまで放り上げるかについて任意性が残っているからである（めちゃめちゃ高く打ち上げてもいいのである）。

プロ選手と花子さんの「ボールが最も高くなる時の地上の位置」はそれぞれ「２」と「２－１／８ｐ」であるのだが、もしかしたら「ｐの値が分からないからどっちがＭに近いかは決まらない（つまり③）」としてしまうかもしれない。
だがちょっと落ち着いて考えてみてほしい。Ｃ２は上に凸なのでｐは具体的な数字はわからなくても確実にｐ＜０である。だから正解は②となる。

（２）

３点目（点Ｄ）が決まるので、ａの値が求まることになる。Ｃ２については全く計算する必要なし。
最後はシュートの高さを比較させるのだが、近似値が与えられているのでこれで計算するだけ。

第３問（選択問題）場合の数

（１）～（４）

最初の方はただ①～④に入れられる色の数を確認して掛け合わせるだけ。（４）は実は②～⑥が赤と青で埋め尽くされるということに気づけば組合せの考えで解ける（なお、①には３通りの色の入り方がある）。

（５）

同色の③と④を大きく〇で囲んでみたらわかりやすいだろうか。あとは余事象みたいな考え方で誘導に乗っていけばいい。

（６）

まともに考えるとかなりの難問だけど、（５）で考え方を丁寧にレクチャーしてくれているのでこれを応用していく。
一つ少ない場合の数を使っていくところなんかは数列の漸化式みたいな感じである。

第４問（選択問題）整数の性質（最大公約数・最小公倍数）

数が大きくなるので途中で計算ミスとかしないように注意。ケアレスミスするとかなり気づきにくい。

（１）

素数や正方形の問題は素因数分解や最小公倍数を求めれば済むのだが、長方形の問題は文字を使わないと厳しい。
横：４６２=２*３*７*１１、縦：１１０＝２*５*１１なので、横にｘ枚、縦にｙ枚みたいな感じで文字を置いていく。
横と縦の長さの差の絶対値を

｜４６２ｘー１１０ｙ｜＝２２｜２１ｘ－５ｙ｜

と変形していけば、｜　｜の中身が±１になるときが差の絶対値が最小になるときとわかるはず。

縦の長さが２２長い場合は絶対値の中身が「ー１」になるときなので、

２１ｘ－５ｙ＝ー１⇒５ｙ－２１ｘ＝１

５の倍数の一の位は０か５しかないので最小の自然数ｘは４だとわかる。

（２）

これも最初は最大公約数・最小公倍数の問題。

こっちの正方形は文字を使わないと大変。正方形ができるときは縦も横も２３１０の倍数になることが分かっているので、赤をｐ枚、青をｑ枚使うとすると４６２ｐ＋３６３ｑも２３１０の倍数、ということで

４６２ｐ＋３６３ｑ＝２３１０ｒ（ｒは整数）

とおくことができる。これを簡単にして

１４ｐ＋１１ｑ＝７０ｒ

こういうときの整数ｐ、ｑ、ｒの探し方にはコツがあって、移項して共通の約数でくくって「〇＝△」という両辺に項が１つずつの状態に整理していく。

この問題では１４ｐを移項して７でくくると「１１ｑ＝７(１０ｒー２ｐ)」となるので、「１０ｒ－２ｐ」が１１の倍数になるようなｐ、ｒの組み合わせを探していけばいい。

第５問（選択問題）図形の性質

まずは図を描くのが一番大事。（１）なら用意してある参考図にガシガシ書き込んでいけばいいが、（２）は問題用紙の余白などに自分で描いていく必要がある。

（１）

接線と円の半径が直交する、対角の和が１８０°の四角形は円に内接する、などはもはや常識ということでいいだろう。
次は描いた図を眺めて、∠ＤＥＧと∠ＤＯＧが弧ＤＧに対してそれぞれ円周角と中心角になっていること、ＯＦがＤＧに直交することからＯＦが∠ＤＯＧの二等分線になっていることに気づけば埋められる。ここまでくれば「カ」はすぐである。