【解法暗記の方法】青チャートをつかった勉強法【実践編】

豊田市周辺にお住まいの皆様、および武田塾生の皆様こんにちは！
逆転合格専門の予備校・個別指導塾の武田塾豊田校です！

前回の【数学は暗記】青チャートを使った勉強法【学習計画編】で青チャートは解法を覚えることが大事、解法を覚えるために使うのだとしつこくしつこく述べたわけですが、そもそも何をもって「解法を暗記した」と言えるのかが謎だと思います。

解法暗記は初めての問題でも解けるようにするためのただの手段に過ぎないということを念頭に置きつつ、何ができれば解法を暗記したことになるのかを考えてみましょう。

解法の特徴を言葉や絵などいろんな手段で説明できるか

結論をいうと、「解法の特徴を言葉や図といったさまざまな方法で説明できる」ことが、解法を覚えたといえることの必要十分条件でしょう。

取り組んだ参考書は完璧にする、つまり、一度やった問題に関してはできるようにすることは前提ですが、私達の最終的な目的は参考書をマスターすることではなく、初見の問題でも解けるように、プロセスを考えつけるようにすることなのです。

ただ、参考書に書いてある解法のまとめ的な部分を覚えるだけでは、初見の問題に応用することは難しいでしょう。

『青チャートI』例題77 （※2021年現在のものとは違います）を取り上げます。

問題：関数 f(x) = x^2-2x+2 の a≦x≦a+2 における最大値 M(a) と最小値 m(a) の式で表せ。

さて、問題の解法はどのように説明されているかを見てみましょう。チャートでは問題の解法は「指針」として書かれています。

指針：この問題では、区間の幅は2で一定であるが、aの増加とともに区間全体が右に移動するから、軸 x=1 と区間の位置関係を調べる。場合分けの方針は以下の通り：

最大（区間の端） → 軸が区間の中央より右、中央、中央より左

最小（頂点または区間の端） → 軸が区間の右外、内、左外

文字だけで見るとなんのことかさっぱりではありませんか？

字面をそのまま覚えるだけでは、実際に初見の問題を解くときに今までに覚えてきた解法をうまくすり合わせて使うどころか、思い出すことすら困難だと思います。

字面を覚えるために学習するのではなく、詳細なストーリーや頭の中に図を思い浮かべ、たくさん動かして、さまざまな方法で理解し、経験的に身につける、要するに「身体で覚える」ことが大事だと言いたいのです。

言葉でざっくり流れを説明できるようにする＝身体で覚える

実際に、例を通して、経験的に解法を習得してみましょう。

解答の流れを細かく整理することで、初見の問題でもどういう手順でとくのかを考えられるという、計画立案能力も身につけられます。

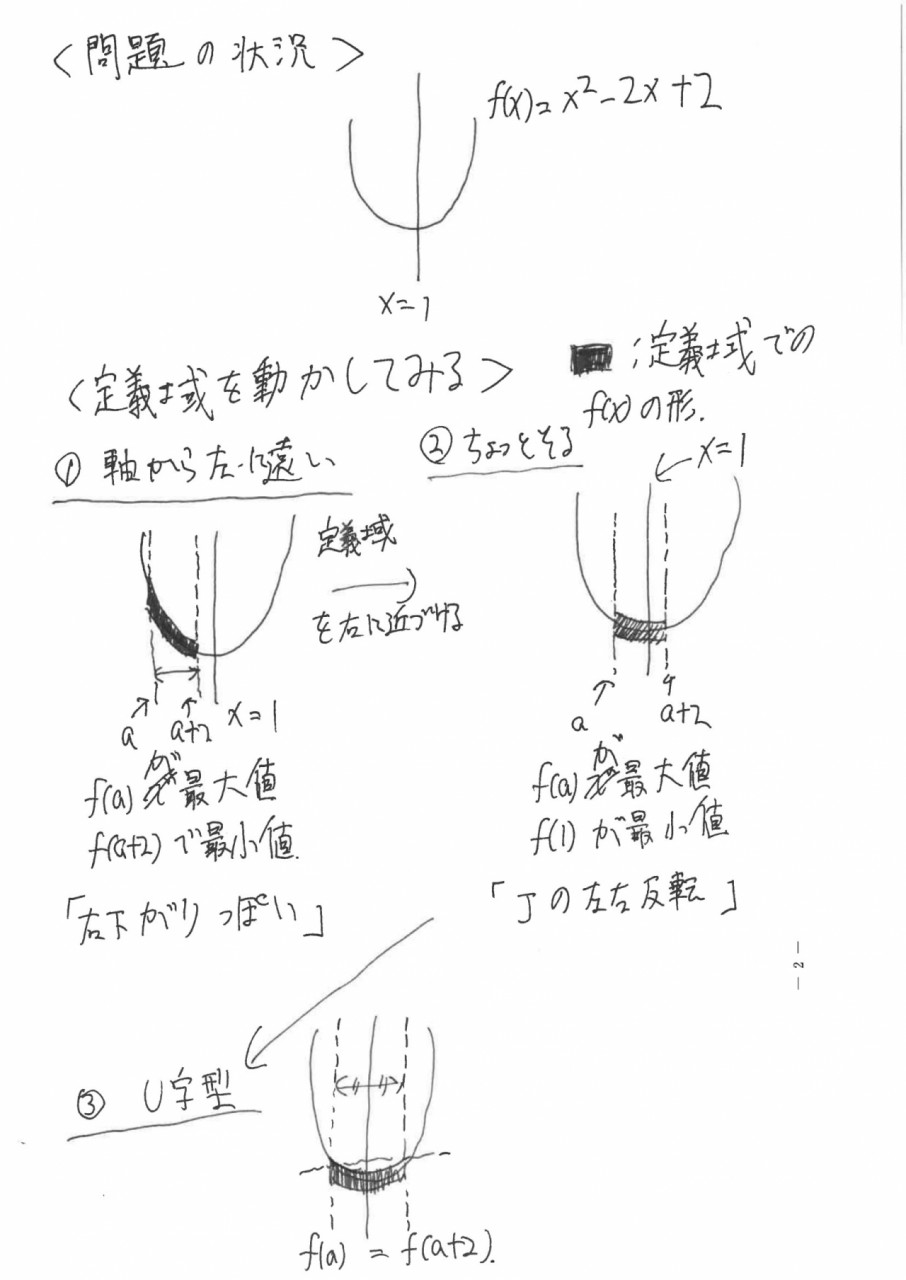
問題の状況

まず、関数は下に凸（=U字）で、軸は x=1 だということは簡単にわかります。

それから、a が増えると、区間の幅はそのままで、区間全体が右にうごくし、a が減ると区間全体は左に動くということがわかります。

定義域を動かしてみる

<軸から左に遠いところに>

軸から左に遠く離れたところに定義域があるように考えてみましょう。

つまり、定義域の右端 a+2 は軸の値 1 よりもずいぶん小さいということです。

定義域の右端の値が軸の値よりも小さい時、定義域で関数は右下がりの直線っぽい形状になっています。

曲がっているが反ってはおらず、最大値は定義域の左端、最小値は右端でとる。

徐々に軸に定義域を近づけてみましょう。

<定義域の右端が軸に到達、関数がちょっと反る>

関数がちょっと反る、つまりアルファベットの「J」を左右反転させたような形状になっています。

最大値は定義域の左端、最小値は軸。

<さらに右に進めて定義域で関数が「U」字型に>

最大値は定義域の右端と左端で、最小値は軸で

…と、定義域を徐々に左から右にずらしていき、最大値と最小値が切り替わるタイミングを考えれば答えを求められる。

絵で考えてみる

言葉で説明したことを図解してみましょう。

頭の中で、関数を思い浮かべ、定義域が動いていくときの最大値、最小値の変化がアニメーションとして理解できればよいのです。

SKM_C25821021320160-1

解法の流れをよく理解すると

以上、言葉で見るのと、絵で理解することの２つの方法で問題解法を経験的に理解し、使える形で覚えることができるようにしました。

これらの理解の仕方を組み合わせて結局私達はどんな解法を身につけられたかを見てみましょう。

1. まずは関数の形や定義域がどんな状況かを理解する…下に凸か、上に凸か、軸はどこか、定義域はどんな風か

2. 定義域が動くことがわかったので、遠いところから動かしていけば場合分けが完成する

応用編

ちなみに、今回の問題では、定義域を動かしたときにどういう変化をするかを視覚的に理解できればよいわけですが、これを身につけると、「定義域は動かず、関数自体がうごくパターンの問題」にもそのまま応用することができます。

関数が動く場合とは、相対的には定義域が動いているというシチュエーションと言い換えてもよいわけです。

また、電話で0565-41-8558（日除く昼1時から夜10時まで）までご連絡ください！
武田塾豊田校は、自学自習を身につけていき、進化を遂げる君たちを徹底的にサポートしていきます❕
武田塾豊田校の全く新しい環境で君も目指す姿に進化しよう！
もちろん、相談会に参加されたとしても、入塾の強制、勧誘等は一切ございませんのでご安心ください。