こんにちは!武田塾豊中校です。
今回は、2023年11月18日(土) 近畿大学で行われた
公募試験の数学を解いてみた!です。
受けた人は是非読み直してみてみてください。
自分の解答根拠と見比べてみてください!

2023年11月18日(土) 近畿大学 公募 数学
配点
100点
時間
60分
形式
マーク式
難易度
変化なし 基礎レベル~標準レベル
問題量
変化なし (18問)
総評
少し捻って考えないといけない問題が結構ありました。
そして、いつも通り計算量はめちゃくちゃ多いです。
煩雑な計算をどれだけ正確に解けるかと
普段の正攻法で解けない問題に対して、どれだけ考える時間を取れるかが勝負になってくる問題だったかと思います。
問題構成 全4題 【()の数は小問数】
1,小問集合(7)
2,確率(6)
3,微分と関数(5)
大問1 小問集合
問1 n進数
アイウエ 2024
オカキク 4224
31044(5)
=3*5^4+1*5^3+0*5^2+4*5^1+4*5^0
=2024
0.2024(5)
=0*5^0+2*5^-1+0*5^-2+2*5^-3+4*5^-4
=0.4224
n進数の問題です。
基本的な考え方は基礎問題精講にてきちんと理解していきましょう。
問2 図形
ケコサ 108
シスセ 1+√5/2
ソタチツ √5-1/4
5角形の内角の和は
180*(5-2)/5=108
n角形の1つの内角は
180*(n-2)/nで求められるのでこれを使う
また、1つの角度は108°と求まったが、
これをcosにそのまま使うことは出来ず、余弦定理は使えない。
図形の性質を利用して問題を解く必要がある。
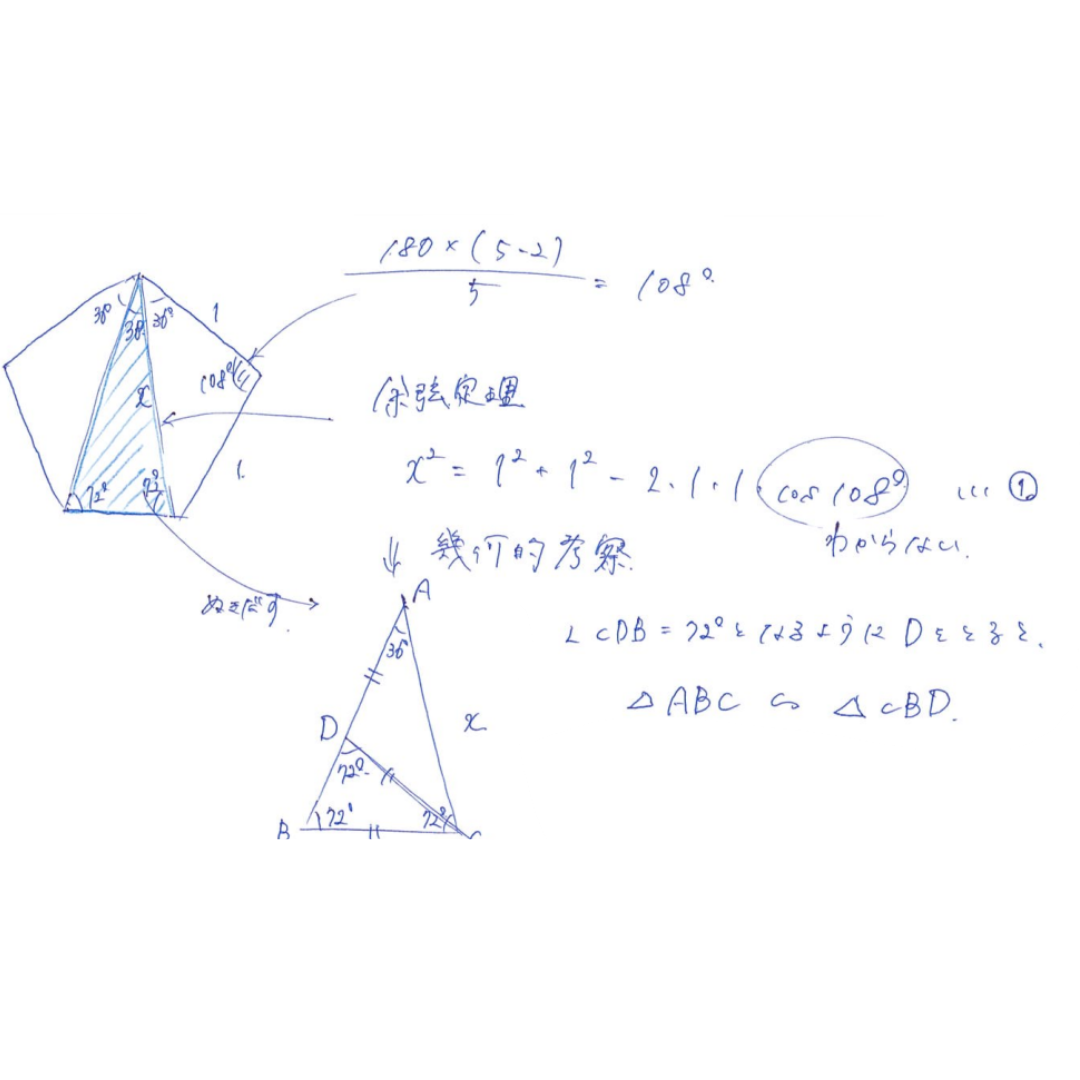
よって
AB:BC=x:1
CB:BD=1:BD
⇒BD=1/x
AD+DB=ACより
1+1/x=x
⇒x^2-x-1=0
解の公式 x>0より
x=1+√5/2(対角線の長さ)
AからBCに垂線をおろし、Hとすると
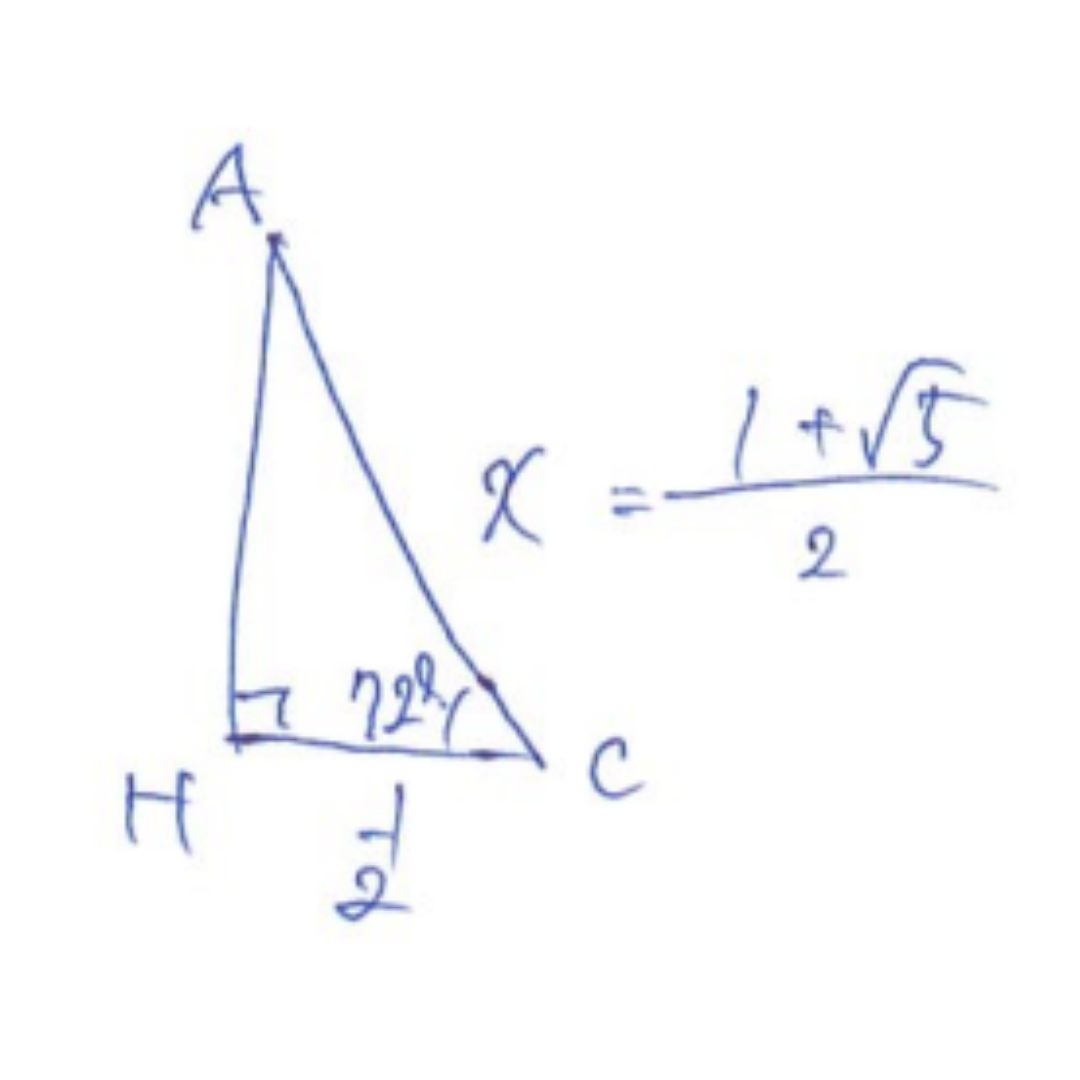
図よりcos72°=1/1+√5=√5-1/4
対角線の長さは黄金比になるので、
かなり計算されている問題なのではないだろうか。
余弦定理を使わず、高校受験時代の図形知識を使う必要があるので、
わすれている人は、基礎問題精講よりも
やさしい中学数学などの図形問題を解いておきたいところ。
問3 平面ベクトル
テト 50
ナニ 10
(ブログだとベクトルの矢印は表せないので、普通の数式で表します)
a+b=(3,4,5) a*b=0
(a+b)^2=|a|^2+2*a*b+|b|^2
3^2+4^2+5^2=|a|^2+2*0+|b|^2
|a|^2+|b|^2=50
a*b=0よりa⊥b
|a|+|b|=kとする
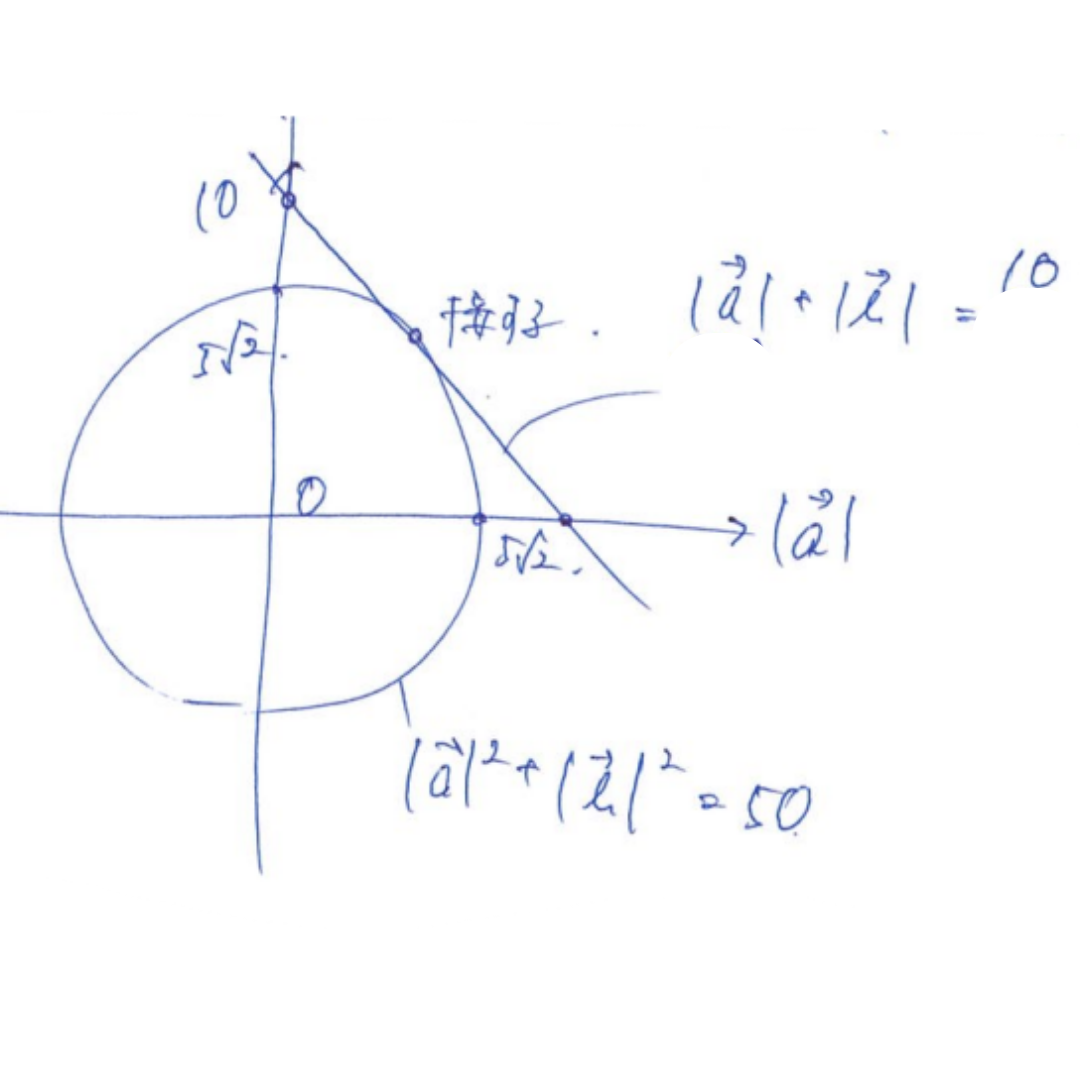
よって最大は図のように
直線が接するときなので、10
大問2 確率
赤玉と白玉を使った検証をする問題です。
問1
アイ 1/4
2/4*2/4=1/4
問2
ウエオ 1/64
1/4*(1/4*1/4)
=1/64
問3
カキク 7/32
(A,B)=(R,R)→(W,R) (パターン1)
=(R,W)→ × (パターン2)
=(W,R)→(W,W) or (R,R)(パターン3)
=(W,W)→(W,R) (パターン4)
のパターンがあるので、
(1/2*1/2)*(1/2*1/2)+(1/2*1/2)*(1/4*3/4)+(1/2*1/2)*(3/4*1/4)+(1/2*1/2)+(1/2*1/2)
=1/8+1/2*3/16
=7/32
各パターンを考えるのは若干面倒ではあるが、
書き出すことで整理できるはず。
書き出すことをめんどくさがってやらないのはマイナスでしかないかと。
問4
ケコサシ 17/32
(A,B)
=(R,R)→(R,R)or(W,W)(パターン1)
=(R,W)→(W,R) (パターン2)
=(W,R)→(R,W) (パターン3)
=(W,W)→(W,W),(R,R) (パターン4)
となるので、1/4+9/32=17/32
(別解)
(2)、(3)で2回目の試行を出しているので
余事象から
1-(2/64+7*2/32)=17/32
ともなる。
問5
スセソタ 7/512
2回目でAの箱にR,R,R,W
3回目でAの箱にR,R,R,R
とする必要があるので、
(1/4*1/4)*7/32*1/4*1/4=7/512
問6
チツテトナ 29/256
AとBの区別なく箱の組を考える必要がある。
また、パターンとしては3パターンが考えられるので、1つ1つ見ていこう。
(A,B)
1回目 (R,R,R,W)(W,W,W,R)
2回目
(R,R)(W,W)→(R,R,R,W) (W,W,W,R)☆
(R,W)→(R,R,R,R)(W,W,W,W)★
この2パターンがあり、ここから更に分岐される。
3回目 ここからパターンが分岐するので要注意。
☆(R,W)→(R,R,R,W)(W,W,W,R) パターン①
★(R,W)→(R,R,R,R)(W,W,W,W) パターン②
★(R,R)(W,W)→(R,R,R,W)(W,W,W,R) パターン③
パターン①
(1/2*1/2)*(1/4*1/4)*1*2
パターン②
(1/2*1/2)*(3/4*1/4+1/4*3/4)*(1/4*1/4)*2
パターン③
(1/2*1/2)*(3/4*1/4+1/4*3/4)^2
パターン①と②は最後に*2があるので要注意。
よって、29/256
大問3 微分積分
一般的な微分積分の問題でした!
計算ミスが無いようにと細かい場合分けを考えてあげる必要がありました。
問1
アイウエオカキク x^3+2x^2+(3c+14)x+2c+16/3
g(x)=3∫ t^2+cdt+2x^2+2c+14x+16/3
=3[1/3t^3+ct](x-0)
=x^3+2x^2+(3c+14)x+2c+16/3
問2
(i)ケコサシ -16/3
∫{x^3+2x^2+(3c+14)x+2c+16/3}dx=c
[x^4/4+2x^3/3+3c+14x^2/2+2cx+16t/3]=c
(4+16/3+6c+28+4c+32/3+16)=c
9c=-48
c=-16/3
(ii)スセソタチ -2+√10/3
g(x)=x^3+2x^2-2x-16/3
g'(x)=3x^2+4x-2=0
x=-2±√4+6/3
=-2+√10/3
(iii)ツテ 15
トナニヌ 37/12
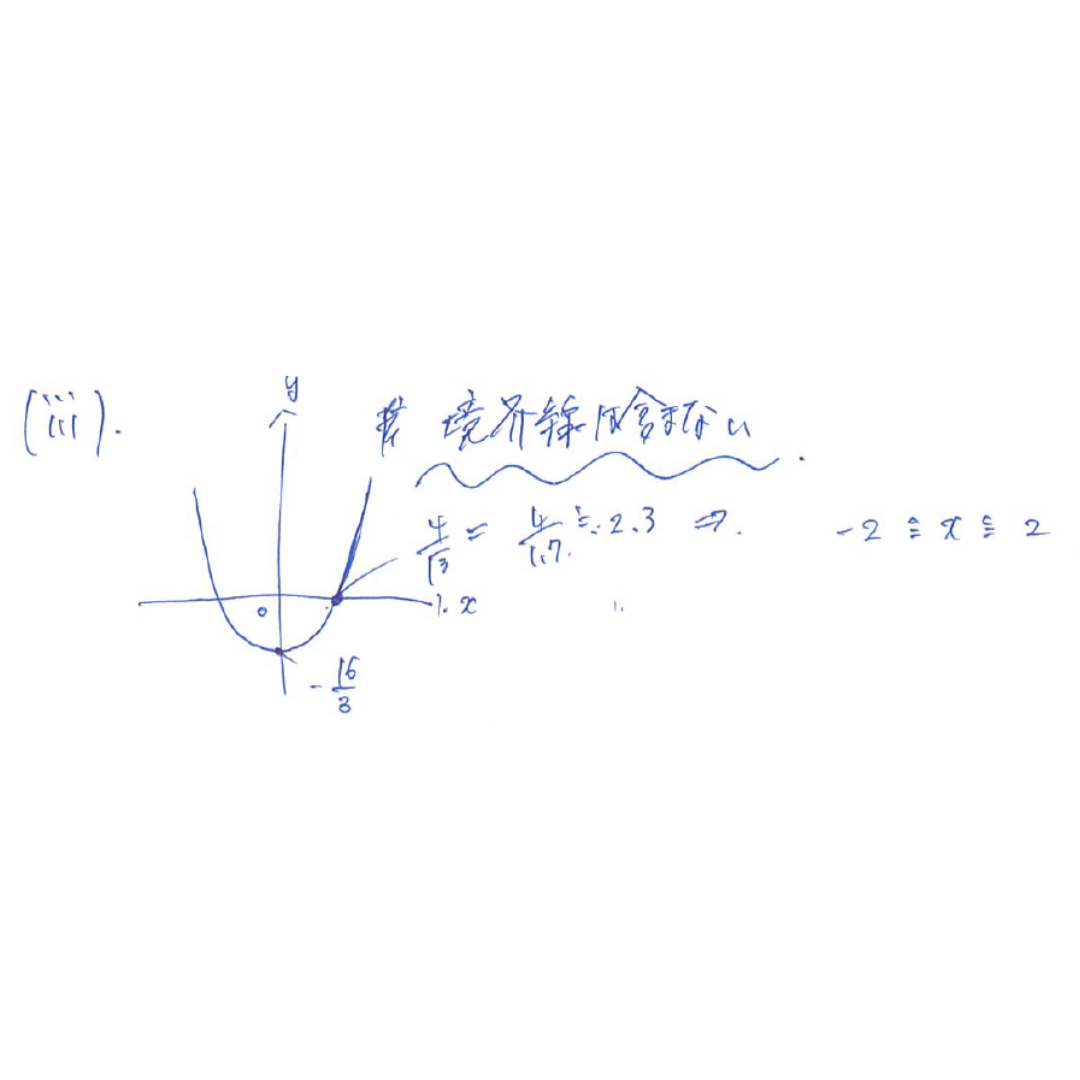
f(+2)<y<0
f(+1)<y<0
f(0)<y<0
の範囲で検討する必要がある。
また、xがマイナスの範囲に関しては、対称であるのでプラスの座標分×2で求めたい個数が決まる。
f(+2)=-4/3 →(2,-1)×2
f(+1)=-13/3 →(1,-1)(1,-2)(1,-3)(1,-4)×2
f(0)=-16/3 →(0,-1)(0,-2)(0,-3)(0,-4)(0,-5)
→よって15個
また、曲線y=f(x)と曲線y=g(x)で囲まれた2つの部分の面積の和は
f(x)=x^2-16/3
g(x)=x^3+2x^2-2x-16/3
h(x)=g(x)-f(x)
=x^3+x^2-2x
=x(x-1)(x+2)
=0
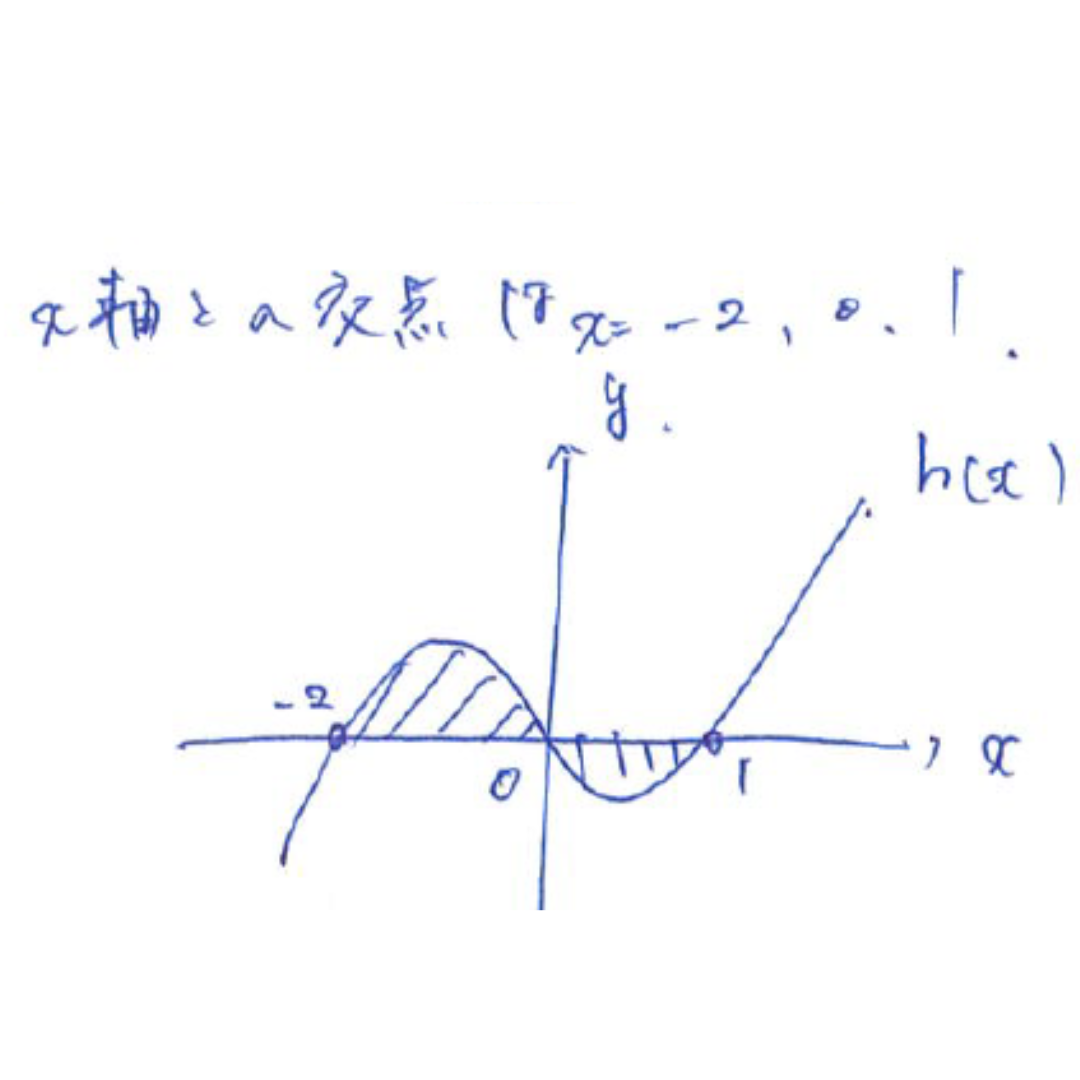
S=∫0→-2(x^3+x^2-2xdx)ー∫1→0(x^3+x^2-2x)dx
=[x^4/4+x^3/3-x^2]-[x^4/4+x^3/3-x^2]
=0-(4-8/3-4)-(1/4+1/3-1)
=8/3-(-5/12)
=37/12
まとめ
以上
いかがでしたでしょうか?
基本的な概念をいかに使えるか、
応用問題を知っているかより、どうやって知識を活かすかが重要になる問題が多かった印象です。
まだ入試は始まったばかり!
しっかり基礎を固めてこの問題を解いていってください!















