こんにちは!
逆転合格の武田塾豊中校です。
今回のブログでは、
2023.2.25(土)に実施された京都大学二次試験の数学についての講評を行います。
確実に得点したい問題や点差の着きそうな問題、難問などに分けて評価します。
ぜひ参考にしてください!

京都大学 文系数学
問題の形式
問題数
記述 5問
解答時間
120分
難易度
標準的(若干の上昇)
全体講評
昨年度に対し、問題や記述の量が増加したという点で難易度はやや上がっています。
計算の量が多い中で繊細な論述に気を配らなければないため高得点は難しく、
手応えよりも得点の伸びにくい問題セットでした。
特に2、4、5は類題の演習経験が大きく差をつける問題です。
1 小問集合

昨年度はありませんでしたが、1つの大問に2つの独立小問を課す形式が今年度は復活しました。以下ではそれぞれの小問について評価します。
問1★ 確率
余事象の典型問題です。
問題文を「サイコロをn回投げて少なくとも1回は5の目が出る」と読み替えましょう。
確実に得点したい問題です。(理系3(1)と共通)
問2★★★ 数と式 式と証明
分母に3乗根を含む式を有理化する問題です。
このままでは考えにくいので3^1/3をxとすると、x^3の値は3であるため
(問題の値)=ax2+bx+cの恒等式の形で表される有理数a、b、cの値を係数比較で求めることができれば結論が得られます。
ここまでの流れに不慣れな受験生が多いと思われる上に、
最後の三元一次連立方程式の計算はやや煩雑です。
別解として式変形を繰り返して分母から3乗を消す方法もありますが、これも難しいです。
2★★★ 空間ベクトル

空間内の2直線が交点をもつ条件の立式は、見慣れない受験生が多かったかもしれません。
要は「4つの点が同一平面上にある」ということなので、
本問では点Rが平面CPQ上にあるという立式で求められます。
この時ベクトルの1次独立に関する記述は忘れないように注意しましょう。
これまでの演習量で差がつく問題だと思います。(理系2と共通)
3★★★★ 三角関数

(1)はいわゆる2倍角、3倍角の公式を加法定理から導出する問題で、確実に得点したい問題です。
公式を暗記して答えだけを書いた答案では減点あるいは無得点だと思われます。
どの公式にも言えることですが、定義から定理や公式を導出する流れで理解する習慣を持って学習をすることが必要です。
(2)は本セットの最難問です。
一辺の長さは三角比を用いて表すことができますが、難しいのは五角形に関する角度での正弦や余弦の値を実数で表す手法です。
一度cos36°の値を求めた経験がないと厳しいでしょう。
以降は辺の長さを不等式で評価していきます。
4★★★ 数列

数列の一般項を和の関係式から一般項を求める問題で、番号を一つ上げて差をとる手法が用いられます。
本問ではこれにより和の漸化式を作ることができるため、和の一般項から数列の一般項を求めることができます。
漸化式は類題の経験が必要でやや難しいですが、大きく差をつけることができる問題です。
5★★ 積分法

整式とそれを含む定積分に関する等式の問題です。
定積分から定数xを排除したときに残るyの定積分が定数であることを忘れなければ簡単な式に帰着させることができます。
計算がやや煩雑なので計算ミスに注意しましょう。
京都大学 理系数学
問題形式
問題数
記述 6問
解答時間
150分
難易度
標準的(平年並み)
全体講評
典型問題が多かったため、昨年度よりは解きやすかったと思われます。
問題にほとんど誘導がないぶん、日頃の演習量が解きやすさを左右したはずです。
6(2)以外は途中まで回答はできると思うので、いかに部分点をもぎ取るかが合否を分けると思います。
1 小問集合

文系と同様に、こちらも独立した小問が復活しました。
問1★ 積分法
定積分を計算する問題です。
計算が煩雑なのでそこは注意が必要ですが、部分積分を正確に行えば得点できます。
計算ミスが痛いので、多少時間をかけてでも見直しをして確実に得点しておきたい問題です。
問2★★ 数と式
x2023-1の剰余を求める問題です。
因数分解ののちに被除数の中に除数のかたまりを作ることができるかどうかを検討します。
確実に得点したい問題です。
2★★ 空間ベクトル
文系2との共通問題です。そちらを参照してください。
空間内で直線が交わる条件については、理解した上で演習を重ねておきましょう。
これも半分以上の得点が望ましいです。
3★★ 確率

(1)は文系1問1との共通問題です。そちらを参照してください。これは落とせません。
(2)は(1)の発展問題ですが、ぜひ得点したい問題です。
Yが3で割り切れる事象と5で割り切れる事象について
ベン図を書いて考えると漏れなく立式することができます。
4★★★ 微分法
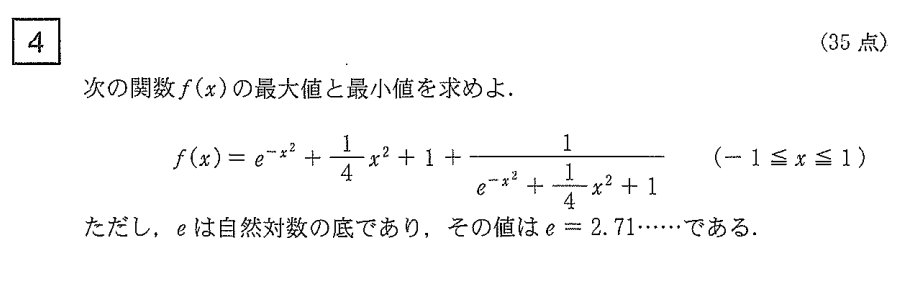
関数の最大最小に関する問題です。
見ての通りf(x)=g(x)+1/ g(x)の形で、f‘(x)とg’(x)の符号が一致することからg(x)の増減を考えればいいことがわかります。
これに気づかなくとも、g(x)の増減を調べることをきっかけにする発想でg’(x)を求めるところまではたどり着いてほしいです。
ちなみに相加平均と相乗平均の関係で解こうとした受験生もいるかと思いますが、今回は使えません。
なぜならg(x)>1のため等号成立条件のg(x)=1と矛盾するからです。
5★★★★ 積分法

線分が通過することによってできる立体の体積を求める問題です。
類題演習経験の差が出る良問だと思います。
求める立体がyz平面対称なのは問題から明らかなので、yz平面に平行な断面を積分する方針で考えます。
断面の円盤の半径を考える過程では文字の設定や立式の根拠に関する論述が難しく、また最後の定積分の計算はやや煩雑です。
6★★★★★ 三角関数

(1)は文系3(1)の類題で、加法定理から導出します。
確実に得点してください。
(2)は本セットの最難問です。
論述する上で難しいのは結論が与えられていないという点で、pは3以上の素数という条件が解答にどう結びつくのかがわからなくなると思います。
大まかな方針としては、一旦題意をみたすm、nが存在すると仮定して背理法により実際はm、nが存在しないことを示します。
論述の中で(1)の誘導からcosnθがcosθのn次式で表されることとそのn次の項の係数が2n-1であることを見出し、
それらを数学的帰納法で証明する必要があります。
この証明が難しい上に、その結論がpの条件と矛盾することを述べなければなりません。
試験時間中に完答することができた受験生は少ないと思いますし、
この問題はできなくてもあまり差は開かないはずです。
この問題は捨ててその分の時間を他の問題に充てるなど、
適切な総合得点を上げるための時間配分にも慣れていきましょう。
まとめ
いかがでしたでしょうか。
京都大学を目指すのであれば、当然勉強時間を取り、
必要な戦略を立てて実際の問題にも取り組まなければいけません。
基礎を固めるのは当たり前、応用問題や実戦問題をどれだけ多くの時間、どれだけ多くの量、京都大学レベルの問題をこなしたかで
合否が変わってきます!!!
京都大学を目指して、やり切れるところまで取り組んでいきましょう。
・今、何から勉強したら良いか分からない
・学校の授業だけでは不安
・この参考書の次は何をしたら良いのか分からない
・今進んでいる勉強が大学受験に向けてできているのか不安
上記に当てはまる人は、必ず武田塾の受験相談に来てください!
受験までの日数はどんどん近づいています。
この時間貴重な時間を無駄にすることなく、
勉強の質を上げられるように、今からしっかり勉強の時間の取り方や、効率的な勉強の仕方を理解していきましょう。

















