皆さんこんにちは、武田塾新安城校です!
まずは、ブログのテーマにもある通り、数学嫌いの方に面白さを伝えていきたいなと思うのですが、
その前に少しだけお話ししようかと思います!
僕はアニメ・漫画が大好きで、家には漫画2000冊以上あるんです!
時々、二次元に行きたいなと思い、自分自身に微分して、次元を下げたいと感じるんですよね。。。
微分する際、三次元に少し自分の欠片を残さないと、積分して戻ってくる際にどこかおかしくなってるかもしれないですね!!
・・・
と、談笑はここまでにして、今回僕自身が感じる、そして、思う”数学の面白さ”について書いていきたいと思います。あくまで僕個人の意見です。
※数学の解き方を教えるのではなく、今回は数学に対する見方を変えるブログです!
嘘をついてもいい???
この見出しを見て「んん?」と思った方もいると思います。
・・・
確かに、現実の世界で”嘘をつくこと”はあまり良くありません。
しかし、数学の世界ではありなんです!!
数学の世界では、"ないものにたいしては何を言っても正しい”というのがあるんです。
例えば、ある人があなたに対して、
「俺の姉ちゃん、新〇結衣似のめっちゃ美人なんだけど、どうやらお前のことが好きなんだよ。一回でいいからデートしてやってくれないか?」・・・
と言われたら、悪い気はしないですよね!むしろウェルカムですよね!
しかし、実際のところ実はこの子は一人っ子で、姉なんて存在していないんです。
現実でこんな嘘をつかれたら発狂しますよね!
が、しかし、数学の世界では大丈夫なのです。
これぞ、『ないものには何を言っても正しい』つまり、「存在しないものには何を言ってもただしい」ということなのです。
さて、ここで皆さんに問題です。
「次の図形のなかで対角線を持つものを答えよ。」
1.正方形 2.長方形 3.正三角形 4.台形
ここまで読んでくれた皆さんならわかりますよね?
そう、答えは全部です。三角形には対角線は存在しません。なので、何を言ってもいいのです。
まあ、普通ここの選択肢に三角形を入れること自体がおかしな話ではありますが・・・
数学の世界には、このような不思議で面白いこともあるのです。
続いてのテーマです!
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
存在問題
数学が苦手な子には少し嫌なワードかなと思います。が、安心してください。
そこまで難しい話はしません。
まず、数学で一番大事なのが「存在問題」です。
普通に考えればわかることなのですが、解がない問題を解こうとしても意味がないですよね。
数学では、解があるかないかが重要になり、解があるのであれば時間を費やせば解くことができますが、解がないのに時間を費やして考えれば、それは時間の無駄です。
なので、まず数学では「存在問題」を考える必要があるのです。
※大学入試や普通の数学の問題には”解”があるので安心して下さい。
もし、解がおかしくなるのであれば、それはあなたの計算ミスです。
ここで、存在問題の何が面白いのかといいますと、それは「できるとわかってるのであれば時間が解決してくれる」ということです。
例えば、ドラえもんで考えてみましょう。
主人公・のび太は、タイムマシンを使って未来に行き、クラスのマドンナであるしずかちゃんと結婚することを知ります。
結婚できるということを知るので、のび太はしずかちゃんに積極的に接していくことができるのです。
ここで、仮にしずかちゃんと絶対に結婚できないと知っていたら、こんなにものび太はしずかちゃんに対して接することはないでしょう。
未来は変えられますが、変えようとする努力は、僕ならできないですね。
こんな感じに、「存在問題」はやる気にもつながります!
皆さんも、何かを成し遂げるには、まず、その目標が達成した時の自分を思い浮かべてください。
やる気がみなぎってきませんか?
・・・
どうです?数学が少し面白くなりましたか?
まだまだいきます!!
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
不変的!
数学において、何人の人が間違っていると指摘したとしても、論理的に証明できたのであれば、それは正しいことになります。
例えば、現代文の論述問題。採点基準となるキーワードなどはありますが、採点官によっては、満点という採点をすれば、減点する人もいます。
つまり、同じ解答であっても人によって変わることはあるのです。
しかし、数学は人によって変わることはありません。そこが数学の魅力です!
不変的なのは魅力ですよね。100人にみせたら100人とも同じ採点になるのです。
また、数学は納得のいかない人にも、ごまかしなく論理的に説明することができます。
数学が嫌いなひとにとって、加法定理を覚えるのは大変ですよね。
「咲いたコスモス、コスモス咲いた」と呪文のように唱えて覚えましたよね。
しかし、加法定理は絵を描いて、視覚的にとらえることもできます。
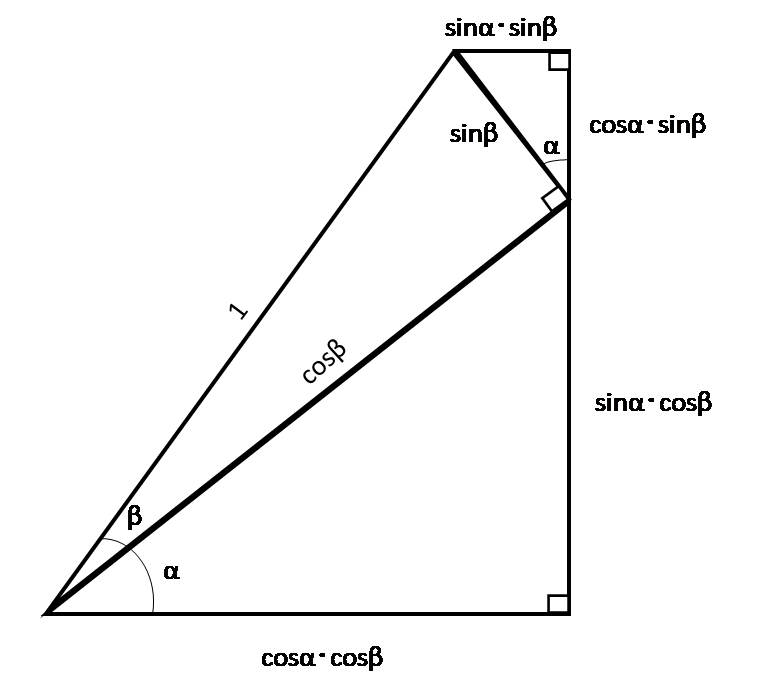
斜辺1、角度α、βの三角形を用意して変形すると、上図のようになります。
そうすると、sinは高さなので
sin(α+β)=cosα・sinβ+sinα・cosβ となり、
cosは横の長さなので、全体のcosα・cosβから余分なsinα・sinβを引くので
cos(α+β)=cosα・cosβ-sinα・sinβ となります。
視覚的に捉えることができますね。授業でもこのように教えてくれれば、苦手になる子を減らせるかもしれないですね!
やっぱり、これ!!
皆さんは、時々ド忘れをすることがあると思います。
その際、自力で思い出せたとき”気持ちいい”と感じることがあると思います。
数学の問題が解けたときの感覚は、僕的にはこの感覚と同じだと思います!
僕自身、難関大学の問題が解けたときには、達成感・高揚感を感じ、発狂することもあります。
また、数学の問題を解いてるときは、時間を忘れ嫌なことも忘れることができます。
数学が苦手な人ほど、自分の実力に見合ってない問題を解き、解答を導けない・解答を導いても正解ではないことに陥っているのではないかと思います。
やはり、”解けない”という感覚を抱いてしまったら、数学を好きになることはできません。
最初は、簡単な問題でもいいので解いて、正解をする喜びを感じることが大切だと思います。
”解ける”と感じれば、楽しさ・面白さを味わうことができ、数学に対する苦手意識がなくなると思います。
復習の仕方!
学校の先生によく、「最後の仕上げに、自分より理解していない人に向けて教える感じで復習しろ」と言われたことはありませんか?
実際、この勉強の仕方は正しく、身につきます。
ただ、同じ問題をもう一回解くというのはモチベーションが下がることもあるかと思います。
その際に、こんな復習の仕方もあるという例を紹介します。
あこがれの人や好きな人に「この問題がわからないんだけどおしえてくれない?」と想像することです。
この方法の利点は、
1.やる気がみなぎる(モチベーションが下がらない)
2.人に教えるという状況なので身についているか確認ができる
この2点です。
この方法はまさに一石二鳥ですね!
数学を学ぶ意味
これまで、数学の面白さ・不思議な魅力について書きました。
ここで、数学を学ぶ意味を書きたいと思います。
よく子どもたちが先生に対して、
「先生面積を求めて何の意味があるんですか?」
と聞く場面がありますね。
確かに、子どもたちの言う通り、大人になって面積を求める場面なんて、ほとんどの人にとってはないですね。
しかし、数学の本質は答えを出すことではないのです。
もちろん答えを出すことも重要ですが、一番大切なのは、答えを出すための
”論理的思考”
なのです!
そして数学を学ぶことで”論理的思考力”が鍛えられるのです。
現在の学校の授業では、短時間で多くの知識を詰め込むものとなっており、ただ、公式を教え意味を教えず、問題を解かせていると感じます。
実際、この方法は効率よく問題を解けるようになります。
しかし、公式の仕組みや成り立ちの説明が不十分であり、多くの生徒にとって、数学はつらい暗記と計算科目になっています。
またこの方法だと、数学で鍛えられる”論理的思考力”が育ちません。
これから、皆さんには数学を勉強する際に、”答えの正解不正解”よりも、答えを出すために”どう考え、どのように解けばいのか”という”論理的思考”を大事にしてほしいと思います。
正しく考え、正しく計算をすれば、必然的に正しい答えが出ます!
これから、数学を勉強する際には”考えること”を大切にしてほしいです。
最後に・・・
僕が感じる、他の教科と数学について話したいと思います!
英語は、勉強することによって世界のつながりができます!
実際僕も、フィリピンに3.4人ほど知り合いがおり、英語で会話しております。
世界共通言語ということもありますし、大学ではほぼ間違いなく英語の講義を受けることになります!
文系・理系に関わらず、今すぐに始めるべき科目だと考えています!
国語は、勉強する意味がないと多くの人は言いますが、母国語を知らないということは大人になった時に恥ずかしく感じる時が来ます。
以前、社会人の友達に「漢字が書けなくて、恥ずかしかった」と言われました。
やはり、母国語は勉強する意味がありますね。
さらには、文章読解能力・・・つまり自分が理解できるように頭の中で言葉を変換したり、処理したりする能力は国語の現代文に精通しているのではと考えています。
ここが育っていないと、他の科目において問われた内容が意味不明・・・ということになりかねません!
理科は、勉強することによって身近なことを知り、一つ一つのありふれたことに対しても、新鮮に感じることができます。
社会は、過去を知り、今の自分にいかせることがあります。
また、知識を広げ、合コンの時とかに、雑学で自慢できることもあると思います。
数学の場合、数学はできなくても、算数さえできれば、生きていくことはできます。
しかし、上記に記したように数学の世界を知ることで、生活が楽しくなるのではないかと思います。
僕が今回書いたブログで、数学に対する苦手意識が無くなったという方がおりましたら幸いです!!!
to be continued .....
この春イチオシ!武田塾の無料受験相談!
中学と高校の勉強ってどう違うの??
大学受験に向けてこの時期にやるべきことは??
この大学とあの大学、ぶっちゃけどっちのが受かりやすい?
勉強のやり方、正直分からないんだけど……
などなど、受験を戦うにおいて有力な情報が
なんと
「無料で」
聞けちゃいます!!
こんなに有力な情報が聞けるのは武田塾だけ!
ぜひ武田塾に来てみてください!
↓お問い合わせはコチラから!!↓
受験相談だけでも意味がある!
入塾しなくても武田塾のやり方で逆転合格していく子もいます。
受験相談を受けただけ、YouTubeで勉強法を学んだだけで飛躍的に成績を上げていく子も実際にいるのです。(このパターンは自己管理をしっかりできる子が多いです。)
受験のアドバイスをもらうだけ、勉強法を聞きに来るだけでも大丈夫です。
必ずなにか役に立てる自信があります。
いつでも無料受験相談を受け付けております。
下記の応募フォームからでも、お電話いただいても、直接校舎に来ていただいても構いません。
↓お問い合わせはコチラから!!↓
ACCESS

|
武田塾新安城校
|
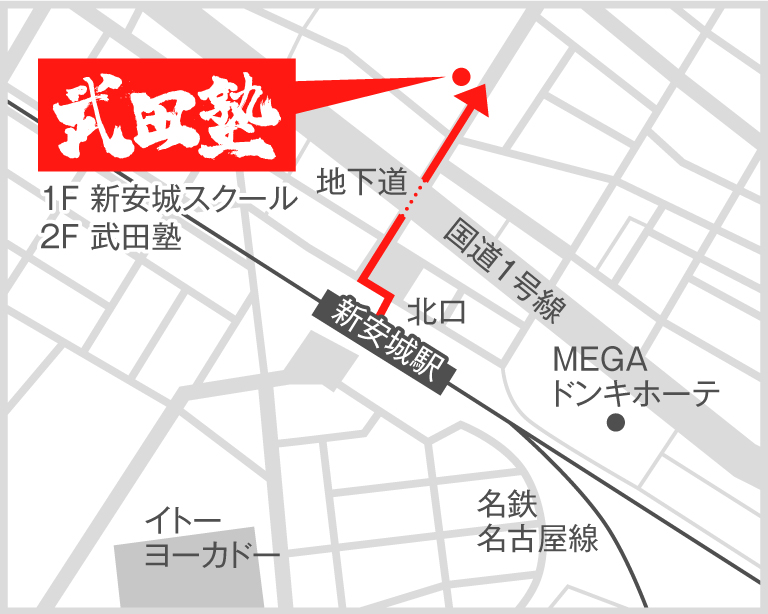
<名鉄本線 新安城駅からのアクセス>
①新安城駅北口をでます。
②そのまま直進し、国道1号線の下を地下道を使ってくぐります。
③駅を背中に北に100m(1分強)向かうと左手に新安城スクール様がございます。
④そのビルの二階に武田塾新安城校がございます。
<お車での来校の場合>
駐車場のご準備が一階(スクール新安城様前)にございます。15・TOEと書いてある駐車場をお使い下さい。











