
共通テストはマーク式。4択問題であれば、分からなくても25%の確率で当てることができます。
それゆえに、共通テスト前後には次のようなオカルトにのめり込む人が一定数います。
自力では合格点を取れないけれど、てきとうに塗った場所が正解で、その分点数が伸びるから大丈夫だ
偶然塗ったところが全部正解なら、○○点くらい増えているはずだ
実際、共通テストで運による点数の上下はどれくらいあるのでしょうか。
私たちは、運要素にどれくらい期待して良いのでしょうか?
1.てきとうに塗って100点取れる確率
全ての問題をてきとうに塗った場合、どれくらいの確率で満点を期待できるのでしょうか。
今回は、2021年本試第1回の英語(リーディング)を例に、その可能性を考えてみます。
2021年本試の特徴
2021年本試験では、このような構成になっていました。
| 問題数 | 点数配分 | |
| 総問題数 | 38問 | 2点×17 3点×22 |
| 4択問題 | 32問 | 2点×14 3点×18 |
| 6択問題 | 1問 | 2点×1 |
| 5択から2択選ぶ問題 | 2問 | 3点×2 |
| 6択から2択選ぶ問題 | 1問(解答欄2つ) | 2点×2 |
| 4つの並べ替え | 1問 | 3点×1 |
| 5つの並べ替え | 1問 | 3点×1 |
問題の8割以上が4択。その半分以上が3点問題。
一見すると適当に塗っても高得点が取れそうな科目です。
では、英語で満点を取れる確率はどれくらいなのでしょうか?
コンピュータに10000回シミュレートしてもらう
執筆者自ら共通テストで実験しても良いのですが、生きている間に満点を取れるか分かりません。
何より、勘で何点取れるかを実験するためだけに人生の貴重な1年を費やしたくない、という思いがあります。
「英語運だけシミュレータ」を作る
そこで、コンピュータにお願いすることにします。

表計算ソフトに問題のデータを入力して、
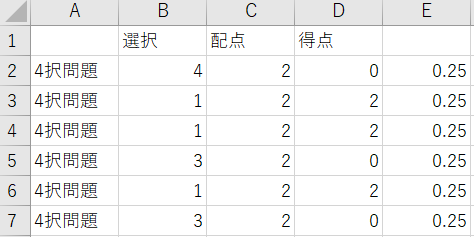
10000回ランダムに塗って、点数を出力してくれるプログラムを作り、

コンピュータに、共通テストを高速で10000回解いてもらいました。
その結果がこちら。

全体のおよそ半分が、平均付近の20~25点。全体のおよそ1/4が、10点台もしくは0点台。
残る1/4は平均点を3点以上上回っているのですが、それでも30点台に到達したのは10人に1人のレベル。
一万人分解いてもらったにもかかわらず、50点台は1人しかいませんでした。
この後5回ほどシミュレーションを回しましたが、57点が最高で、100点を取る人は一度も現れませんでした。
確率を使って計算する
数万回シミュレーションを回しても、100点を取る人は1人もいません。
それどころか60点台すら出てこない始末です。
つまり、勘だけで高得点を取れる確率は、相当に低いことが分かります。
では、100点を取れる確率はどれくらいなのでしょうか。
それぞれの問題の期待値を割り出す
もう一度共通テストの構成を見直してみると、勘で当てやすい問題とそうでない問題があることが分かります。
数字が小さいほど当てやすく、大きいほど当てにくい問題です。
| 問題数 | 点数配分 | |
| 総問題数 | 38問 | 2点×17 3点×22 |
| (1) 4択問題 | 32問 | 2点×14 3点×18 |
| (2) 6択問題 | 1問 | 2点×1 |
| (3) 5択から2択選ぶ問題 | 2問 | 3点×2 |
| (4) 6択から2択選ぶ問題 | 1問(解答欄2つ) | 2点×2 |
| (5) 4つの並べ替え | 1問 | 3点×1 |
| (6) 5つの並べ替え | 1問 | 3点×1 |
(1)4択問題は、4つから1つ選んで当たればよいので、勘で当たる確率は1/4(25%)。
(2)6択問題は、6つから1つ選んで当たればよいので、勘で当たる確率は1/6(約17%)。
ここまでは簡単なのですが、ここから計算が急に複雑になります。
高校生以上の方は数学ⅠAの復習を兼ねて計算してみましょう。
|
Q1. 5択から2つ選ぶ問題では、5つの選択肢から2つを選び、両方正解だった場合にのみに得点が入る(順不同)。この時、得点が入る確率を求めよ。 Q2. 6択から2つ選ぶ問題では、5つの選択肢から2つを選び、両方正解だった場合には4点が、片方のみ正解だった場合には2点が入る。この時、4点・2点を得られる確率をそれぞれ求めよ。 Q3. 4つの並べ替えでは、4つの選択肢を正しい順番で書いた場合にのみ得点が入る。この時、得点が入る確率を求めよ。 Q4. 5つの並べ替えでは、5つの選択肢から4つを正しく抜き出し、それらを正しい順番で書いた場合にのみ得点が入る。この時、得点が入る確率を求めよ。 |
世界中の人がてきとうに塗ったら100点は出るか
筆者が計算した結果は以下の通り。
|
Q1. 5個から2個選ぶ組み合わせなので、5C2=10(通り)。正解は1パターンなので、1/10(10%)。 Q2. 6個から2個選ぶ組み合わせなので、6C2=15(通り)。4点取れるパターンは1つなので、1/15(約7%)。2点取れるパターンは8つなので、8/15(約53%)。 Q3. 4つの並べ替えは4!=24(通り)。正解は1パターンなので、1/24(約4%)。 Q4. 使わない選択肢を正しく選べる確率が1/5。正しく選んでも、4つを正しく並べ替えられる条件付き確率はQ3より1/24。よって、両方を同時に達成できる確率は1/120(約1%)。 |
これらを元に計算すると、筆者の計算が正しければ、
38問すべてを勘で当てられる確率は、約1/400垓となります。
400垓(ガイ)という表記は聞きなれないかもしれませんが、アラビア数字で表記すると、
「400,000,000,000,000,000,000,000」です。
今の世界人口が80億人(8,000,000,000)くらいですから、
「世界中の人間がそれぞれ10兆回共通テストを受ければ、満点が1人出る」くらいの確率。
残念ですが「勘だけで100点を取ることは絶対にあり得ない」と考えて良さそうです。
一万人に一人レベルの豪運をもってしても、50点台がせいぜいといったところ。
時間が間に合わず、てきとうに埋める……上ぶれは期待できるか

現実に戻りましょう。
次に考えるのは、「分からない問題」だけを適当に塗ったケースです。
この場合、点数はどれくらい期待して良いのでしょうか?
「とりあえず塗る」ことに意味はある
もちろん、空欄を埋めることに意味はあります。
問題が全く分からなくても、約23点取れることが証明しています。
では「勘で塗ったら、23%の確率で正解できる」と仮定して、何点伸びそうか計算してみましょう。
| 実力で取れた点数 | てきとうに塗った後 | 点差 |
| 80点 | 84.6点 | +4.6点 |
| 70点 | 76.9点 | +6.9点 |
| 60点 | 69.2点 | +9.2点 |
| 50点 | 61.5点 | +11.5点 |
| 40点 | 53.8点 | +13.8点 |
適当に塗るだけでも、1割近く点数が変化することが分かります。
調子が悪いときほど、最後まであきらめずにマークすることが大切です。
しかし。
期待値以上の点数の伸びを期待してはいけない
「上の表の点数を大きく超えることは期待できない」のです。
勘で当てるハードルは意外と高い
例として、次のようなケースを考えてみましょう。
|
実力で68点取れたものの、分からなかった問題が12問。 分からない12問は、「2点の四択問題×4 3点の四択問題×8」 |
何も塗らなければ68点のままですが、残りを全て塗れば、正解を引く確率は1/4。
普通に考えれば2点問題が1つ・3点問題が2つ当たって、76点まで点が伸びそうです。
では、ここで考えてみましょう。
|
Q1. この人が「てきとうに塗って」、期待値である76点以上を取る確率はどのくらいでしょうか。 (ア)約85% (イ)約75% (ウ)約65% (エ)約55%
Q2. この人が「てきとうに塗って」期待値を5点上回る81点以上取る確率はどのくらいでしょうか。 (ア)約40% (イ)約25% (ウ)約15% (エ)約10% |
見出しのタイトルでなんとなく予想はつくかもしれませんが、とにかく考えてみましょう。
期待値が出れば「ラッキー」
それでは解答です。
|
Q1. この人が「てきとうに塗って」、期待値である76点以上を取る確率はどのくらいでしょうか。 A. (エ)約55%
Q2. この人が「てきとうに塗って」期待値を5点上回る81点以上取る確率はどのくらいでしょうか。 A. (ウ)約15% |
「12問適当に塗れば、期待値で8点取れる」と聞くと、私たちはつい「8点確実に取れる」と思いがちです。
しかし実際には、期待値の8点を手に入れられるかは五分五分。
本当は「期待値通りの点数が得られるかどうかすら怪しい」のです。
ですので「てきとうに塗って期待値以上とれたらラッキー」と考えた方がよいでしょう。
そして、期待値通りの点数を取るだけでもラッキーなのに、それ以上の点数を望むのは危険です。
確かに「期待値より5点以上上回る確率は約15%」と聞くと、可能性がそれなりにあると感じたかもしれません。
しかし、「期待値より5点以上下回る確率はもっと高い」のです。
適当に塗って正解数を水増しするのは、それくらいの博打だということです。
結論
今回は、共通テストにおいて「運による上下があるのか、私たちはどこまで期待して良いのか」検証しました。
共通テストにおいて、運による点数の上下は間違いなくあります。
共通テストはマーク式で、しかも4択問題が多いため、
分からない問題があっても、てきとうに塗れば25%ほど得点できる計算になります。
しかし、そもそも25%得点できるのは「運が良い方」で、
「期待値を大きく上回る」よりも「期待値を大きく下回る」方が可能性としては高いです。
ましてや「勘で塗った問題が全問正解」というのは、まったく現実的ではありません。
「勘で塗った問題が全問不正解」である確率の方がはるかに高いです。
そういうわけで、
「共通テストは運要素はあるものの、幸運に期待したら裏切られる可能性の方がずっと高い」
というのが本記事の結論になります。
夢のない話ですが、「共通テストで確実に点数を伸ばすには勉強しかありません」。
共通テストが不安なら、どの数字の可能性が高いかを調べるのではなく、
どの塾に通えば最後の追い込みができるか調べた方が点数は期待できそうです。
ちなみに、佐賀駅前にある武田塾佐賀校では、高3生・浪人生を対象とした冬期講習の受付を行っています。
11~1月までの好きなタイミングから1ヶ月単位で始められるので、
共通テストの点数を引き上げたい方はぜひご相談ください。













