アルキメデスが見つけ出した、円周率の値について!
皆さん お元気ですか?
現役で息子を東大に合格させたノウハウや生活習慣管理術などを中心に、
大学入試の問題解説などもおこなっております!!
今回は、大学入試で出題された数学問題の内、
特に取り上げるに値する良問につき解説していきたいと思います。

良問① 2003年度に東京大学理系で出題された次の問題
問題:円周率が3.05より大きいことを証明せよ。

何故最初にこの問題を取り上げたかというと、
この2003年度は私の息子の大学入試の年で、
「お父さん、面白い問題出たよ。でも僕は工夫して完璧に解けたから安心して!」
と言っていたのが今でも耳に焼き付いているからです。
幸い彼はこの年に現役で東大に合格しました。
この問題は、この年に出題された数学入試問題での注目度No,1となりました。
さて、皆さんだったらこの問題をどう解きますか?
東大受験生達は、意外にできが悪かったそうですが、
私からすれば、かなり簡単な問題です!!
解答へのアプローチ 2パターン
アプローチとして自然に浮かぶのは、半径1の円と、
その円に内接する正n角形との比較から証明する方法です。
数学の問題を解く際には、様々な解法を考える必要がありますが、
この問題の場合は、主に2つのアプローチが考えられます。
先ずは、最も多くの受験生が考えた解き方から説明します。
解答へのアプローチ 「解き方1」:
半径1の円の円周の長さと、正n角形の外周の長さとの比較
半径1の円の円周の長さは、2π。
またこの円に内接する正n角形の1辺の長さをaとおくと、余弦定理より、
a² = 1² + 1² -2・1・1・cos(360°/n)
ここで、n=12のとき、つまり、正12角形の場合、
a² = 2-2 cos 30°= 2-√3 ----- ①
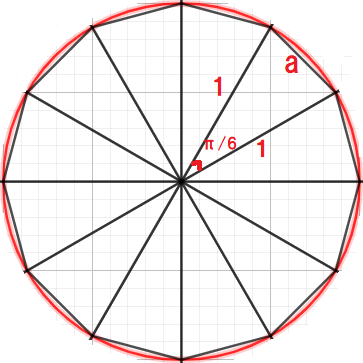
半径1の円の円周は、それに内接する正12角形の外周より大きいから、
12a < 2π よって、6 a <π両辺を2乗すると、36 a² <π² ------②
①を②に代入して、36 (2-√3 ) <π²
ここで、1.73 < √3 < 1.74 であり、2-√3 のとりうる値の範囲は、
2-1.74<2-√3<2-1.73である。更に3.05²= 9.3025であるから、
36 a²= 36 (2-√3 ) > 36 (2-1.74) = 9.36 > 9.3025 = 3.05² ----- ③
②と③より、3.05² < π² つまり、3.05 < π

解答へのアプローチ 「解き方2」:
半径1の円の面積と、正n角形の面積との比較
半径1の円に内接する正n角形の面積Snは円の面積π(ぱい)より小さい。
また、正n角形の一辺に対する中心角は、360°/ n である。
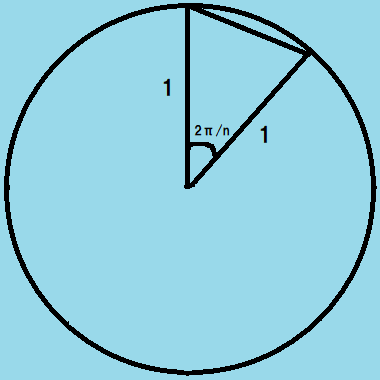
頂角が360°/n、二つの辺の長さが各々1である二等辺三角形の面積は1/2*1^2sin(360°/n)である。
よって、正n角形の面積Snは、
π > Sn = (n /2) sin(360°/n) -----①
上式の右辺に計算し易いようなnを代入して、3.05より大きくなるようにすればよい。
n= 24とおくと、①式は、
π > 12 sin15°= 12 sin(45°- 30°) = 12 (sin45°cos30°- cos45°sin30°)
= 12(√2/2・√3/2 - √2/2・1/2 ) = 3 (√6 - √2 )
ここで、√6 は 2.44より大きく、√2 は 1.42より小さいから、
π > 3 (√6 - √2 ) > 3 (2.44-1.42) = 3.06
問題文の条件が円周率の値が3.05より大きいことを示すことを求めていたので、
3.06>3.05
よって、円周率πは、3.05 より大きい。
どうですか。 全然難しくないでしょ!
この2つの解答を見てすんなり理解できなかった人は、数学の基礎が身に付いていない
人です。先ずはしっかり基礎を勉強し直しましょう。
次回は、別の良問についてのお話をする予定です。
東大生を育てたパパ講師が教える 「良問解説」はいかがでしたか?
この記事を最後までお読みくださいまして誠にありがとうございました。
このご縁を大切にしていただけたら嬉しいです。
東大志望者だけではなく、名大、名工大や有名私立大学を目指す君は
是非、武田塾瀬戸校へお越しください!!
そして新スタートに正しい勉強法が学べる武田塾をお選びいただくのも一つの方法です。
↓↓↓↓↓↓↓↓
武田塾瀬戸校からのお知らせ <無料受験相談実施中!!>

武田塾瀬戸校は学力を上げる正しい勉強法が学べます。
学力を上げるための仕組みを正しく理解し、
学力を飛躍的に上げるための、正しい勉強方法と効率的な勉強計画を実践すれば、
志望校合格に向けて、必要な学力を最短で身に付ける事ができます!
武田塾では、それを実現することができます!!
★今の勉強方法に不安がある。
★どんな参考書を使ったらいいのか?
★今から受験勉強を始めて、間に合うのか不安がある。
★どの科目から手を付ければいいのかわからない。
★志望校の選択に悩んでいる。
★自分は今から勉強を始めるとして何からしたら良いのか?
★英語や数学などの教科別の効率の良い勉強方法を知りたい。
★国語の点数の上げ方を知りたい。
不安な人のために一人一人の状況に合わせて個別に
具体的なアドバイスをする無料受験相談を行っています。
完全個別相談なので、ご案内できる人数に限りはありますので
今すぐ下記フォームまたは校舎電話にてお問い合わせください。
電話:0561-85-1355
(受付時間13:30~21:00 ※日曜・一部祝日休)
武田塾瀬戸校(逆転合格の1対1 完全個別指導塾)















