こんにちは!
北九州市八幡西区にあるJR折尾駅から徒歩4分、大学受験専門「日本初!授業をしない塾」でお馴染みの武田塾折尾校です!
折尾校 校舎HP:https://www.takeda.tv/orio/
今回は「【九州大学】数学の難易度を評価・分析!合格点や対策を考察!」についてお話ししていきます。

九州大学の数学の難易度分析!
九州大学の数学について、各問題の難易度・目標点を、問題の着目点から考え方まで整理してまとめます!
(※標準的な問題集を完璧にした程での評価です)
大問1 「定点からの接線+定数の範囲」
<難易度>★★☆☆☆
<目標点>45/50
定点から接線を引くのは数2の基本問題。
ただ今回の問題は指数関数の微分という面で数3の問題に当たる。
定数aの範囲を求めようと進めるのではなく、まずは言われたままに接線の式を出してみる。
接線の方程式を満たすための定数aの条件
→定数分離し、解を持つように設定
→分離する際に「0」で割らないことに注意。
→数3の基本知識を使ってグラフを書く
<講評>
受験数学を数多く触れている人ならなんども見たことがある問題。
この問題は完答すべき問題。
グラフを書く際に極限を取るなど、基本的な部分の記述に注意したい。
大問2 「高次方程式の複素数解+整数の絞り込み」
<難易度>★★★☆☆
<目標点>30/50
⑴4次関数の解の一つが虚数解
→共役の複素数を解に持つ
→因数分解
→他の2解をαβとするとわかりやすい
c,dをa,bを用いて表すためf(x)に解を入れるという方針はすぐに出したい。
⑵まずは前半部分に書いてあるf(1)とf(-1)を実際に求める。
すると、f(-1)=3bと極めてシンプルな形になるので、ここから絞り込むと良い。
あとは不定方程式を解き、絶対値で与えられる範囲に留意すればbの値が一つに絞り込める。
→f(1)に代入し同じ作業を繰り返す。
→a,bが求まったら⑴の途中で出てきたαβに代入するとスムーズに
<講評>
⑴は必須!
⑵は情報量に圧倒されずに、できることから着実に進めれば完答も難しくはない。
大問3 「空間ベクトル(内積の計算)」
<難易度>★★★★☆
<目標点>10/50
この問題は間違いなく後回しにするべき!
その判断スピードが九州大学2020数学の分かれ目だろう。
[問題]
・3つの直線がそれぞれ直角
・直接関係のない辺の長さだけ与えられている(点Oとの関係性が見えない)
→与えられた情報から出せる限りの情報を掘り下げて行く
=時間がかかる
⑴2直線(l,m)のベクトルを表す
→直交するから内積0
→式変形の結果から点Oに関する長さがわかる※難
→内積計算ができるようになる
→内積の定義式を用いて角度をだす
⑵ ⑴の計算途中で3つそれぞれの対辺の長さが等しいことに気付けるか?
→等面四面体(全ての面が合同)の性質を利用 ※普通習わない
圧倒的捨て問!
<講評>
数学はゴール(求めたいもの)から逆算し、わかるものから計算していくパズルゲームです。
この問題は結果的に解ける問題ではあるが、見通しは立てづらく、ミスが許されない入試では手をつけたくない問題。
ベクトルを得点源にする人も多いと思うが、いつもと違う点(必要な情報がすぐ出ていない)に気付いて捨てる気持ちで他の問題を取るべき。
大問4 「整数と集合の確率」
<難易度>★★☆☆☆
<目標点>40/50
⑴25の倍数となる
→5が”少なくとも”2回でる
→余事象を考える
⑵4の倍数となる
→2,6が2回以上出るor4が1回以上出る
→余事象(2,4,6が一回も出ない+2,6のどちらかが1回だけ出る)
⑶100の倍数となる
→⑴かつ⑵であれば良い
→数えだしでも良いが、集合論を持ち入れれば完答に近く
<講評>
⑴⑵は絶対に落としてはいけない!
⑶も考え方自体は難しくはない(標準問題)だが、重複でミスをしないためのロジックが必要となる。
大問5 「空間座標の面積積分+面積の回転」
<難易度>★☆☆☆☆
<目標点>50/50
なんの捻りもない定石問題。
素直に解き進めて行きたいが、練習が足りてない受験生は以下の手順を徹底するように!
[問題]
問題文を最後まで読み、全体像を予め想像しておく(完全にじゃなくて良い)
→全体図をxyz空間座標で書く(あくまで整理するだけ)
→x,y,zのうちどれで区切るべきか?
→関数であれば共通した文字で区切ると良い
→平面に書きおろす
→いきなり「x=tのとき」が難しければ、
一番わかりやすい値で考える「x=0のとき」など。
⑴「x=tのとき」と指定された
→まずはわかりやすいように「x=0のとき」のyz平面をかく
→今回の問題であれば(0,2,2)から(0,0,0)の直線で区切られる
→x=tのときも区切られる線は変わらず、円柱Eの断面積が変わる。
→あとは面積をtの関数
→tの範囲に注意して積分
⑵面積の回転
→回転の中心から一番遠い点と近い点を明確に
→ドーナッツ型の円の面積を求める
→tの簡易に注意して積分
<講評>
この問題は必解問題です!
なぜなら、順番を正確に守って計算を進めれば『想像力なんて必要なく、確実に解けるから』です。
唯一思考力が必要とされる問題として例を挙げると「3つの平面に関しての条件式が出てくる時」東大で過去に出たことがあるレベルです。
空間が苦手な人は多いです。
そもそも想像つかないから計算しやすいように平面に落とし込むやり方があるのです。
”物理と同じように”ルールを守って解く練習をしましょう。
受験数学では絶対に完答したい問題です!
総評
九州大学の数学対策をする上で、『特別な知識』はいりません!!
学科によって科目ごとの配点が変わりますが、数学の5問構成で、得点を均一配分するのは変わりません。
九州大学2020年の数学では、7割は取るべき問題内容でした。
九州大学に限らず、国公立の過去問演習を繰り返せば十分に得点できます。
また、150分も与えられているので、わからなくても焦らず、完答を作っていくことが最後の勝敗を分けるでしょう。
==========================================
毎年「易化した!」「難化した!」と騒がれますが、自分がやってきた勉強に対して、冷静に分析しましょう。
共通テストに向けてなのか?例年と傾向が変わったのは事実ですが、傾向が変わっても対応できるように受験勉強に励みましょう。
受験勉強は「合格確率を上げる」作業です。
自分の強み・弱みを分析した上で、本当に必要な事に時間を費やしましょう。
数学は特に分析が難しい教科です。
(分析できている人は必然と高得点取れます)
少しでも数学に不安がある方は、武田塾折尾校までお問い合わせください。
校舎長があなたに必要な事を見極めてアドバイスします!
正しい過去問の使い方・数学の勉強法はこちら↓
武田塾の数学ルートは最短最速!?
他大学の分析
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー

武田塾では、九州大学や九州工業大学、北九州市立大学などの福岡県内の国公立大学を始め、東京大学、京都大学、一橋大学、大阪大学、東京工業大学、東京医科歯科大学、北海道大学、東北大学、お茶の水女子大学などの最難関国公立への逆転合格者を多数輩出しています。
また私立大学では、地元の西南学院大学、福岡大学はもちろん、早稲田大学、慶應義塾大学、上智大学、東京理科大学、明治大学、青山学院大学、立教大学、中央大学、法政大学、学習院大学、関西大学、関西学院大学、同志社大学、立命館大学などの超有名私立大学への進学者も多数います。
関東や関西地区で広まっている武田塾だからこそ、地元進学者以外にも手厚いサポートや、合格カリキュラムの作成が行えます。
他の塾や予備校にはない、武田塾の個別サポートシステムを利用して一緒に合格を目指しませんか?
******************
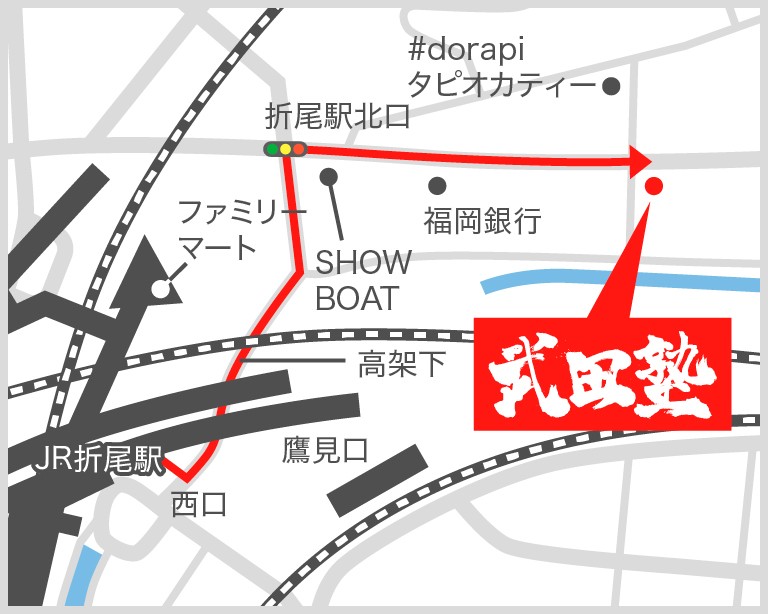
武田塾 折尾校
〒807-0825
福岡県北九州市八幡西区折尾1-14-5
安永第一ビル
TEL:093-616-8400
FAX:093-616-8401
******************













