【🌸逆転合格🌸】
武田塾岡山西口校です。
無料受験相談
大好評の無料体験特訓
実施中!
・来年こそ合格を狙う既卒生!
・現役合格を目指す高3生!
・今から勉強したい高1・高2生!
・もちろん中学生も!
~合格したい方!~
~真剣に勉強したい方!~
~勉強法を知りたい方~
【お問い合わせ】
086-250-3375
または
↓↓↓↓↓↓↓↓↓↓↓↓
からどうぞ!
今回のテーマ
【物理 大学受験 】
力学の基本を固めよう

大学受験物理で最優先の
【力学】
➤確実に点を取れるようにしたい!
受験の物理は【力学に始まり力学に終わる】
力学の特徴
・他の単元に通ずる
(電荷の運動,原子,音など)
・入試で確実に出題される
・出題されるモデルが可視
【力学のジャンル】
・ 位置,速度,加速度
・ 力のつりあい
・ 運動の法則
・ エネルギー
・ 運動量
・ ≪いろいろな運動≫
・ 円運動
・ 楕円運動
・ 単振動
など
今回、モーメントのお話を少ししようかと思います。
モーメント
【モーメントとは】
・ 物体を回転させようとするもの
➤力ではない
【モーメントの要素】
・ 回転の支点
・ 力の作用点
・ 力の作用線
(今回の話に出てきます)
・ 支点から作用点までの距離
・ 作用点での力の大きさ
回転させるためには

≪図1:引張り≫
ペンの左端(カチャカチャする方)を支点
ペン先を作用点
・ 矢印の方向へ力を加える。ペンは回転するか?
➤回転しない

≪図2:曲げ(片側固定)≫
ペンの左端(カチャカチャする方)を支点
ペン先を作用点
・ 矢印の方向へ力を加える。ペンは回転するか?
➤回転する
【結論】
回転させるためには
支点と作用点を結ぶ線に対して垂直な方向へ力を加える必要が有る
↓
※ 演習問題で
支点と作用点を結ぶ線に対して
力が斜めになっている場合
(平行でも垂直でもない)
何故、力のベクトルを分解するか理由が分かりますよね
↓
モーメントの値(大きさ)を求めるのに必要な要素は
・ 支点から作用点の距離
・ 支点と作用点を結ぶ線に対して垂直な方向の力(大きさ)
↓
モーメントは
これらの積で求めると定義されている
からです。
練習問題
問題
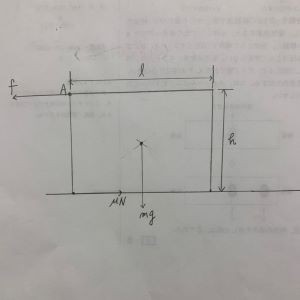
質量mの直方体が水平な床の上に置かれている。
辺の長さは水平がl、高さがhである。
辺A(紙面に垂直)の中点に水平左向きの力fを加え、
fを増加させていくと、直方体は転倒しようとした。
そのときのfを求めよ。
また、直方体と床の間の最大静止摩擦係数μを求めよ。
【力学モデルを理解する】
↓↓↓↓↓↓↓↓↓↓↓↓↓↓
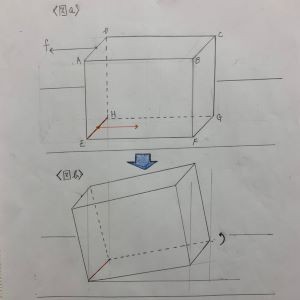
≪図a≫
・力fを大きくする
➤直方体の底面と床の間の摩擦力は大きくなる。
(静止している)
・更にfを大きくする
➤摩擦力が最大となる。
(摩擦力は立体図の赤で示した底面の左側の辺で効いている)
≪図b≫
・それ以上fを大きくした瞬間
➤直方体は赤で示した辺を軸に回転し始める。
(赤で示した線=回転軸)
【簡易モデル化】
↓↓↓↓↓↓↓↓↓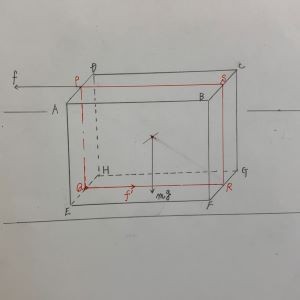
直方体の奥行方向は対称。
➤力fの作用点Pを含む長方形PQRSで考察して良い
(この平面に直方体の重心も含まれる)
解答前の考察
・モーメントの問題と分かる
↓
・力は3種類
(直方体の自重,力f,摩擦力f':全て同一平面上)
↓
・回転支点をどこに取るか決める
(【運動】から【簡易モデル化】したQ点と分かる)
↓
・支点からそれぞれの作用点を結ぶ
↓
・式を立てようとすると…
↓
・力の作用点が同一線上にない?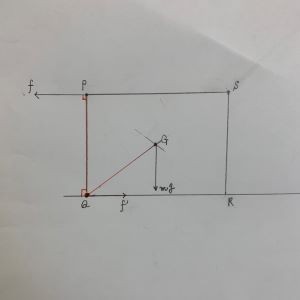
Q点周りに回転させようとした時、
支点と各作用点を結ぶと…直方体の重心G点のみ
同一直線上ではないと分かる。
(解きなれていないと思います)
解説・解答
モーメントの値(大きさ)を求めるのに必要な要素は
・ 支点から作用点の距離
・ 支点と作用点を結ぶ線に対して垂直な方向の力(大きさ)
思い出してください
この定義に従えば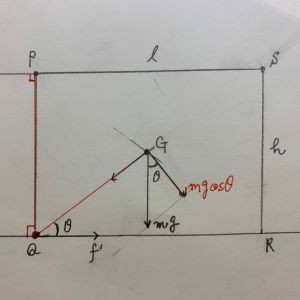
・長方形PQRSの対角線長さをL
・∠SQR=θとする。
・tanθ=h/l
・cosθ=l/L
・sinθ=h/L
【力のつり合い】
f=f'
床と底面での直方体が床から受ける垂直抗力をNとるすと
mg=N
f'=μN
↓
f=f'=μmg
【モーメントのつり合い】
G点での力(自重)は
QGに対して垂直な成分
mgcosθ
↓
≪Q点周りのモーメントN(g)≫
N(g)=L/2・mgcosθ
=mgl/2
≪P点周りのモーメントN(f)≫
N(f)=h・f
反時計周りのモーメントの向きを正とすると
(時計回り正でも支障はない)
Q点周りの合モーメントは
N(f)-N(g)=0
↓
f=mgl/2h
μ=l/2h
(答)
※ 実は、別解もあります。
作用線平行移動の原理
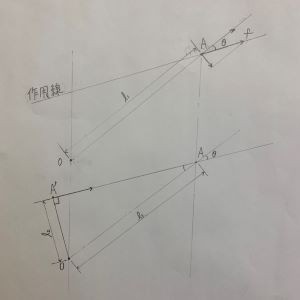
・ 回転支点をO
・ 作用点をA
・ OA=l(1)
・ O点とA点を結んだ直線と作用線の偏角をθ
↓
・ O周りのモーメントN(1)は
N(1)=l(1)・fsinθ
O点から作用線上に垂線を下す。
(→ 交点をA'とする)
ここで
力のベクトルfの作用点をA → A' 平行移動
(OA'=l(2)とする)
↓
N(2)=l(2)・f
△OAA'の三角比より
sinθ=l(2)/l(1)なので
↓
N(2)=l(1)sinθ・f
=N(1)
↓↓↓↓↓↓↓↓
作用線上であれば
力の作用点をどこに平行移動させても
モーメントは不変
(作用線平行移動の原理)
ベクトルが複数になっても原理は不変
↓↓↓↓↓↓↓↓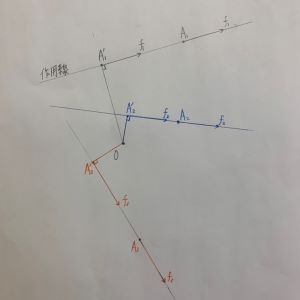
・ 力のベクトル(f(1),f(2),f(3))の支点(作用点)
→ A(1),A(2),A(3)
・O点から作用線に下した垂線と作用線との交点を
→ A'(1),A'(2),A'(3)
・ f(1),f(2),f(3)の支点を
A(1),A(2),A(3) → A'(1),A'(2),A'(3)
➤ 平行移動
原理を応用して
全ての力の作用点を同一直線上に並べることも可能
↓↓↓↓↓↓↓↓↓↓↓↓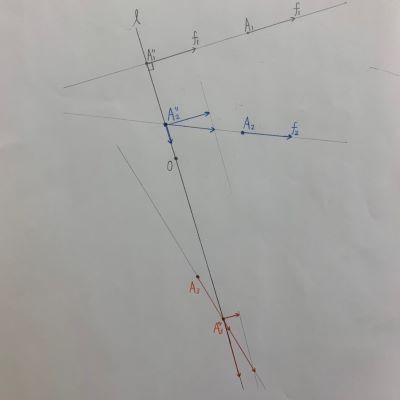
・力のベクトル(f(1),f(2),f(3))の支点を全て
直線l上に集まるように平行移動
(A(1),A(2),A(3) → A'(1),A'(2),A'(3))
↓
f(2),f(3)を分解し
直線lに垂直な成分を求めれば
↓↓↓↓↓↓↓↓
全ての作用点が同一直線上で並んだ状態で解ける
↓↓↓↓↓↓↓↓
解きなれている形へ持ち込める
【注意点】
作用線平行移動の原理
↓
剛体のみ適応可
(※ 剛体については別の機会でご説明できればと)
武田塾で物理を勉強しよう!
使用する参考書
今回紹介したのは
・物理のエッセンス(力学・波動)
から抜粋したものです。
エッセンスは
・ 入試でよく出るタイプの問題が主
・ 各単元中に少し難易度の高い問題もある
・ 演習量が多く、基礎固めには適材
こうしたメリットがあります。また、
・ 解説がさほど丁寧ではない
というデメリットもあります。
いずれにしても、
武田塾参考書の中でも
『確実にためになる一冊』
勿論、このレベルの問題を確実に解けるようになれば
少しずつ参考書の難易度は上げていきます。
参考書だけで足りない部分
今回のように
・塾生個々の質問に対応
しています。
しかし、
各自が今の自分のレベルに合った参考書を使用しているため
・本当にガッツリ教える
というケースはさほどありません。
↓
そこまで教える必要がある
➤ 使用する参考書のレベルが合っていない
ということになりますから。
物理で身に付けて欲しいこと
【いきなり式で解く】
のではなく
【モデルでを理解する】
今回の例で言うと
↓
【力学モデルを理解する】
↓↓↓↓↓↓↓↓↓↓↓↓↓↓
の部分になります。
つまり、
【力学的な構造を理解する】
ということです。
(※ これはすぐに習得するのは難しいです。
しかし、物理を勉強するには是非身に付けて欲しい
2021年度はこのレベルで理解して
素晴らしい成績を残された方もおられました。
↓学力を上げるプロセス:画像をクリック!↓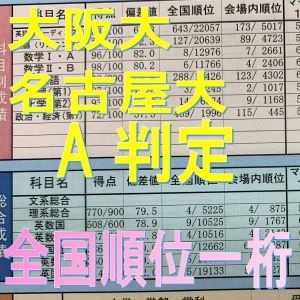
【物理の学力(偏差値)アップ】
・講義系と演習で定義を理解して解いているか
➤常に意識して演習する
・問題で与えられたモデルを理解する
・いきなり式で解こうとしない
↓
・意識付けで能力は上がります
≪余談≫
とりあえず…
ベクトル付の資料を手書きで作成
↓
写真に撮って画像へ取り込む
↓
という作業の連発で……
編集で今回ブログ書くのにクタクタです(**)
物理や化学を記事にするのは難しいかも知れません。
これが最後になったらごめんなさい!
~大学受験塾・予備校なら~
【武田塾岡山西口校】
岡山市北区駅元町30-13横田ビル3F
(岡山駅西口から徒歩2分)
【tel】086-250-3375
【e-mail】okayama@takeda.tv
〈月~土曜日〉
【自習室利用可能時間】13:00~22:00
【電話受付対応時間】 13:00~22:00
〈日曜日〉
休校
















