【逆転合格!】
≪医学部・難関大理系受験はお任せ!≫
武田塾岡山西口校です!
無料受験相談
大好評の無料体験特訓
実施中!
・来年こそ合格を狙う既卒生!
・現役合格を目指す高3生!
・今から勉強したい高1・高2生!
・もちろん中学生も!
~合格したい方!~
~真剣に勉強した方!~
~勉強法を知りたい方~
【お問い合わせ】
086-250-3375
または
↓↓↓↓↓↓↓↓↓↓からどうぞ
本日は
偏差値アップ講座・思考力を上げる勉強法
~複素数平面の攻め方~
数学的思考力を上げたい!
という方、是非ご覧ください。

複素数の定義
「複素数」と聞いて
概念を理解していない方もおられるかと思います。
実部と虚部は同列に表現できないのです。
つまり
実部と虚部はそれ以上纏めることは不可能です。
(※意味合いは異なりますが…
例えば
2x+3yってそれ以上纏めることはできないですよね?
これは、xとyを"別のもの"として扱っているからです)
では、どう表現するか?
実部→横軸、虚部→縦軸
これを平面上に表現する
という定義に至った訳です。
これが複素数平面(ガウス平面)と呼ばれるものです。
ガウス平面は平面ベクトルと概念は同じ
Z=a+ibという複素数平面上の任意の点があるとします。
Zは(a,b)という実部・虚部の2つの成分を有する形になります。
一方、点Aは(a,b)という座標値を有する
つまり、(x,y)という2つの成分を有する形になります
これは、二つの事柄が
幾何的に同じ事を意味する
ということになります。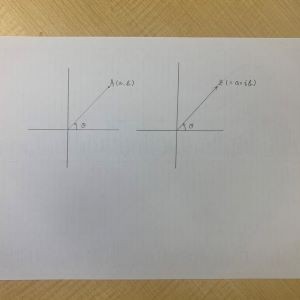
平面の定義
平面のをどう定義するか?
平面とは2次元です。
どうすれば
2次元を定義できるのか?
任意の基準点を定義する。
基準点から2方向に軸を振る
これだけです。
(ちなみに、3方向に軸を決めれば空間です)
あとは
横軸に実数
縦軸に虚数と定義するだけです。
(実際にこの手順でグラフを描いてみてください。
すぐに理解できます)
座標系も理解できる
先程の例で
Z=a+ib
A(a,b)
とすると
原点から複素数Zと点Aまでの距離はそれぞれ
√(a^2+b^2)
となります。
また、座標値が同じという事は
水平軸からの偏角(θ)も同じ
つまり
原点からの長さも偏角も同じ
↓
極座標系で見ても同じ
という見方ができます。
平面上の幾何問題として解く
複素数平面に限らず、
平面問題は
入試では頻出
ベクトルや関数などはその典型です。
今回も問題を準備しています。
複素数の理解を深めて頂ければ
と思います。
なんでもかんでも、いきなり式で解こうとしない
【問題】
複素数平面上の3点、A(1)、B(z),C(z^2)が
鋭角三角形をなすZの範囲を求め、図示せよ。
〈東京大〉
幾何的な検討
いきなり式で解こうとする方
不正解です。
問題自体が
幾何問題です。
【解説】
・問題文のままに
鋭角三角形を書いてみる
(問題文の図示)

問題文の条件から
A,B,Cの最低限の位置関係だけは押さえておく。
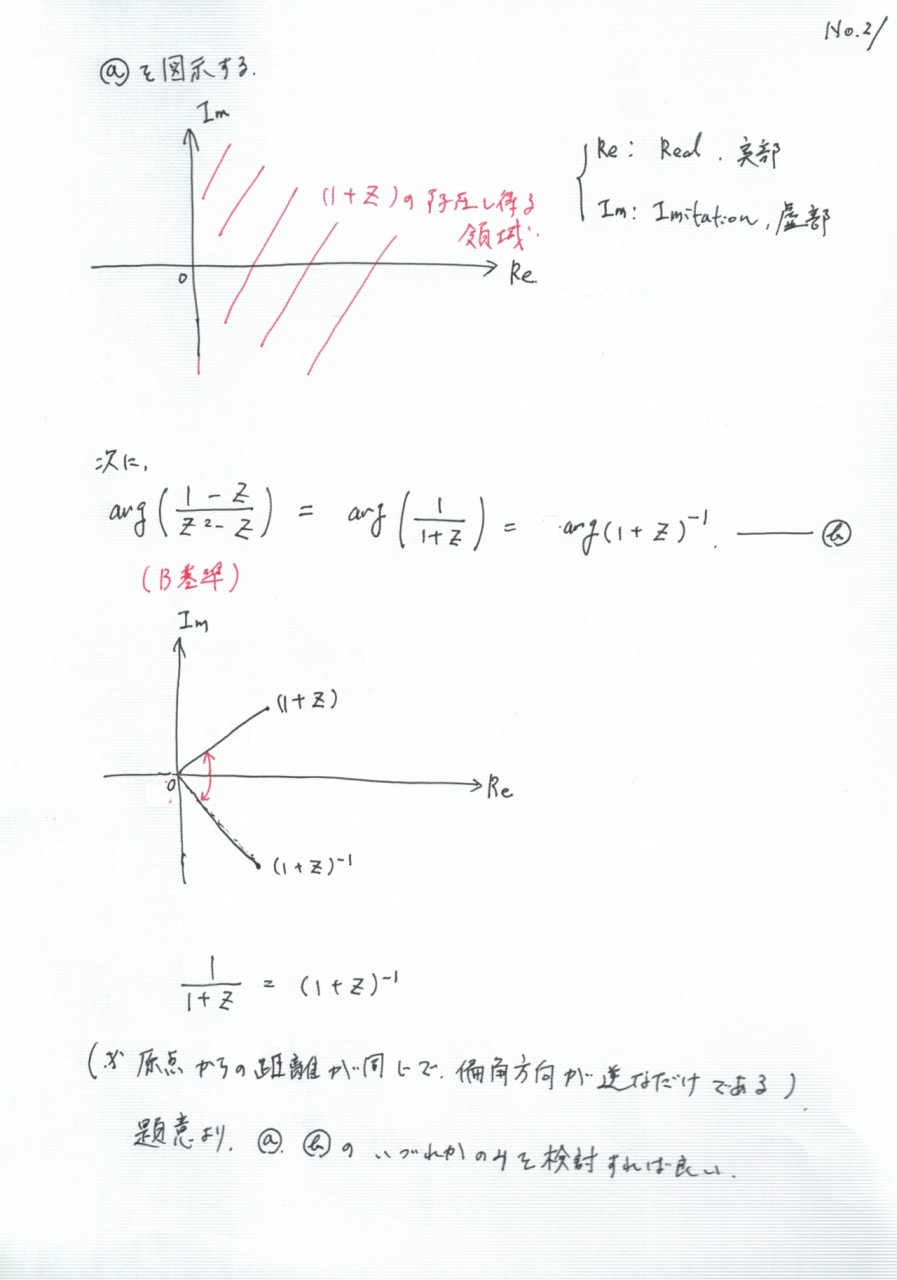
偏角を考えるのに
A基準、B基準で考慮した場合までは検討できた訳です。
(平面上の任意の点を基準点からみて回転)
→ 幾何的な考察
(式で解こうとしていない)
解き方を理解して欲しいんです。
進めていきます
同様にして、他の偏角も求めます。

ここまで来たら
もう要領は掴めているでしょう。
どんどん進めていきます。
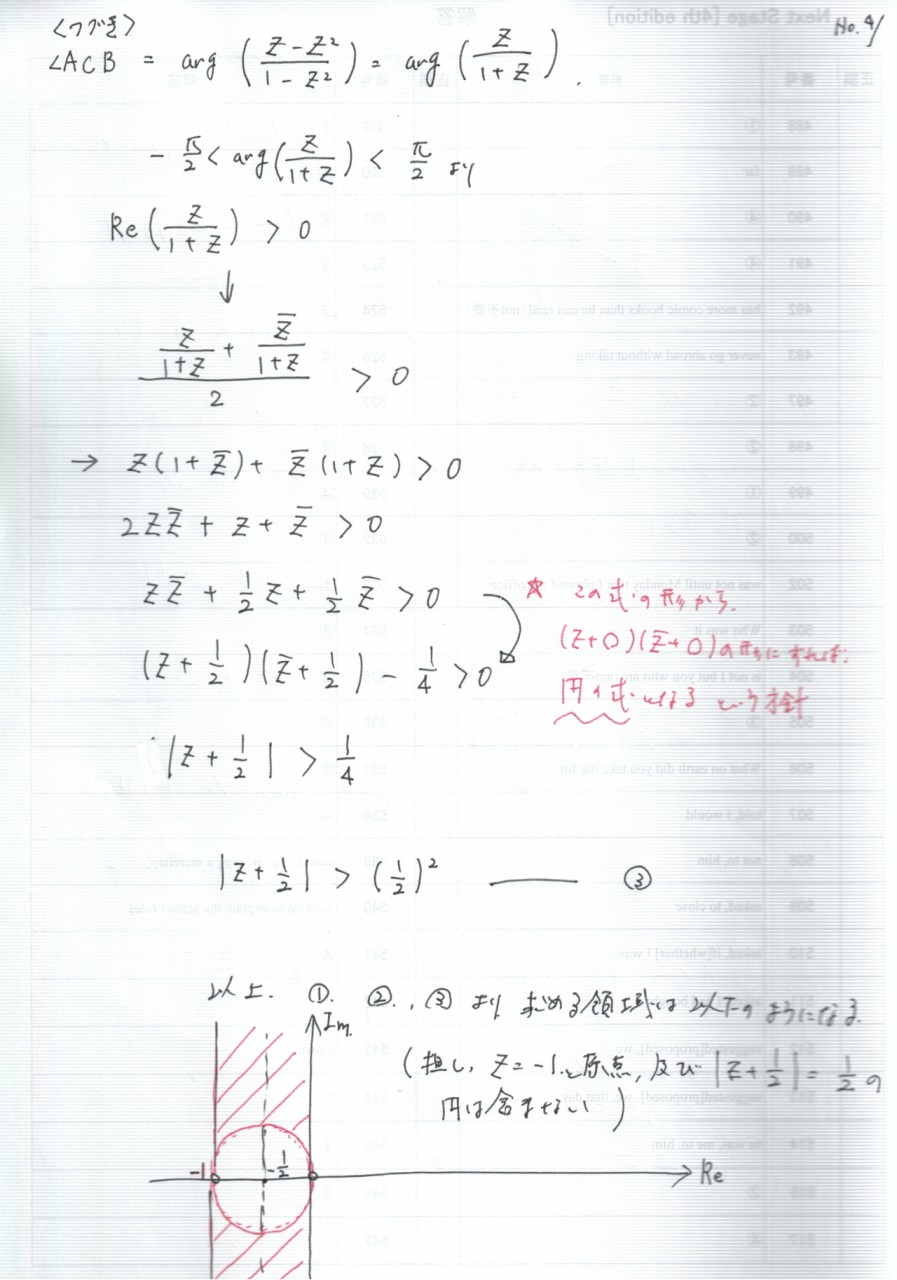
どうでしたか?
シンプルでかつ、幾何的なところを抑えて式を活かす。
一連の流れ、さすがこれを作ったのは東大の人間だけある
と思いました。
しかし
押さえるべきとことはどこなのか?
再度、ご自身でも見直してみてください。
いくら私が解いても、貴方にとっては
「インプット」に過ぎません。
どんな問題でも、マスターするには
自分で演習、即ち
「アウトプット」が必要です。
【医学部受験・難関理系受験】
↓↓↓↓↓↓↓↓↓↓↓↓
武田塾岡山西口校へお任せください!
~大学受験塾・予備校なら~
【武田塾岡山西口校】
岡山市北区駅元町30-13横田ビル3F
(岡山駅西口から徒歩2分)
【tel】086-250-3375
【e-mail】okayama@takeda.tv
〈月~土曜日〉
【自習室利用可能時間】13:00~22:00
【電話受付対応時間】 13:00~22:00
〈日曜日〉
休校














