【逆転合格!】
≪医学部・難関大理系受験はお任せ!≫
武田塾岡山西口校です!
無料受験相談実施中です。
大好評の無料体験特訓も実施中です!
・来年こそ合格を狙う既卒生!
・現役合格を目指す高3生
・今から勉強したい高1・高2生!
・もちろん中学生も!
~合格したい方!~
~真剣に勉強したい方!~
~勉強法を知りたい方~
【お問い合わせ】
086-250-3375
または
↓↓↓↓↓↓↓↓↓↓からどうぞ
今回は
・偏差値アップ講義
・思考力を上げる勉強
数学の「空間図形」です。
苦手な受験生が多いので、
解説します。
空間図形の
解き方をマスターするための参考にしてください。
なぜ、空間図形に対する苦手意識が生じたのか?
空間図形と聞くだけで嫌気がさす………
という方もおられます。
高校数学全体の中でも鬼門かも知れません。
何故苦手になるのか?
「解き方」を知らないからです。

空間図形の「解き方」とは?
私はよく自分の担当している生徒さんにこう言います。
「空間図形は平面に崩せ」
……………???
平面に崩す?
以下で具体例を使って考察します。
平面図に崩す
【問題】
x,y,z空間に A(1,1,0) B(-1,1,0) C(-1,-1,0) D(1,-1,0) P(0,0,3) を与える。
5点を結んでできる立体に対して
x^2 + y^2 >= 1
を満たす部分の立体の体積を求めよ
一般的な
空間図形の手順
(つまり「解き方」)を示します。
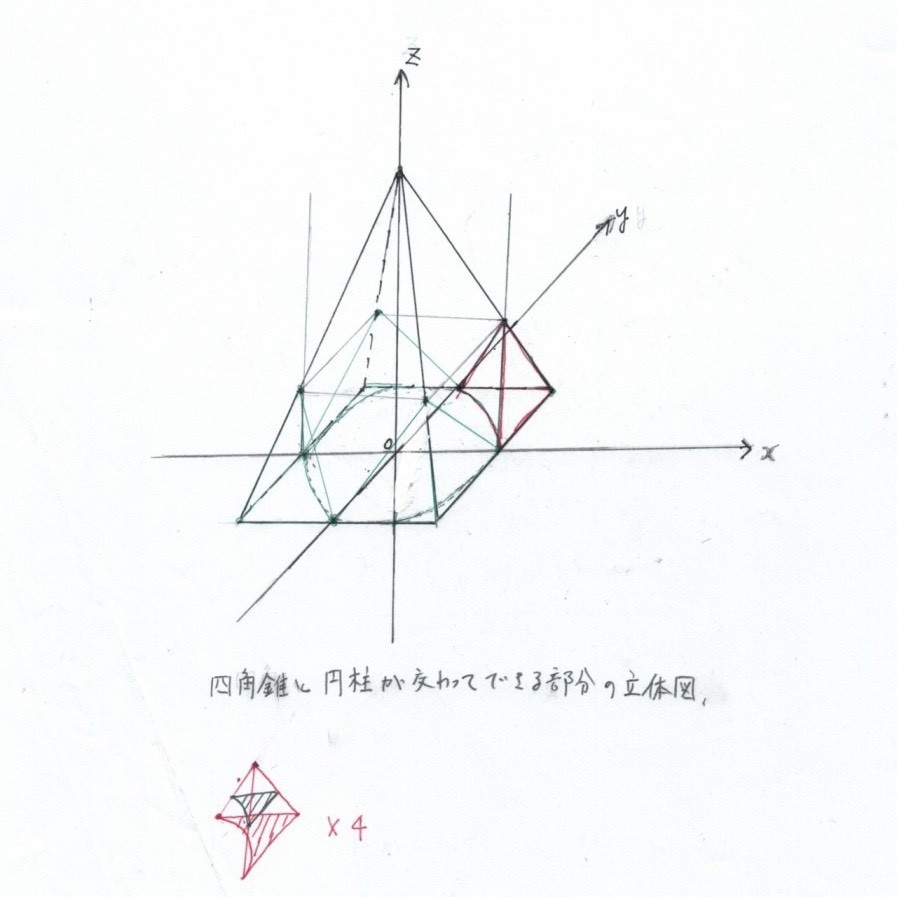
① 問題文で書かれた内容を、そのまま図に書き出す。

【ポイント】
問題で求めたい立体がどのような形状をしているか?
➤ おおまかで良いので書き出す
↓↓↓↓↓↓↓↓
解くのがラクになる!
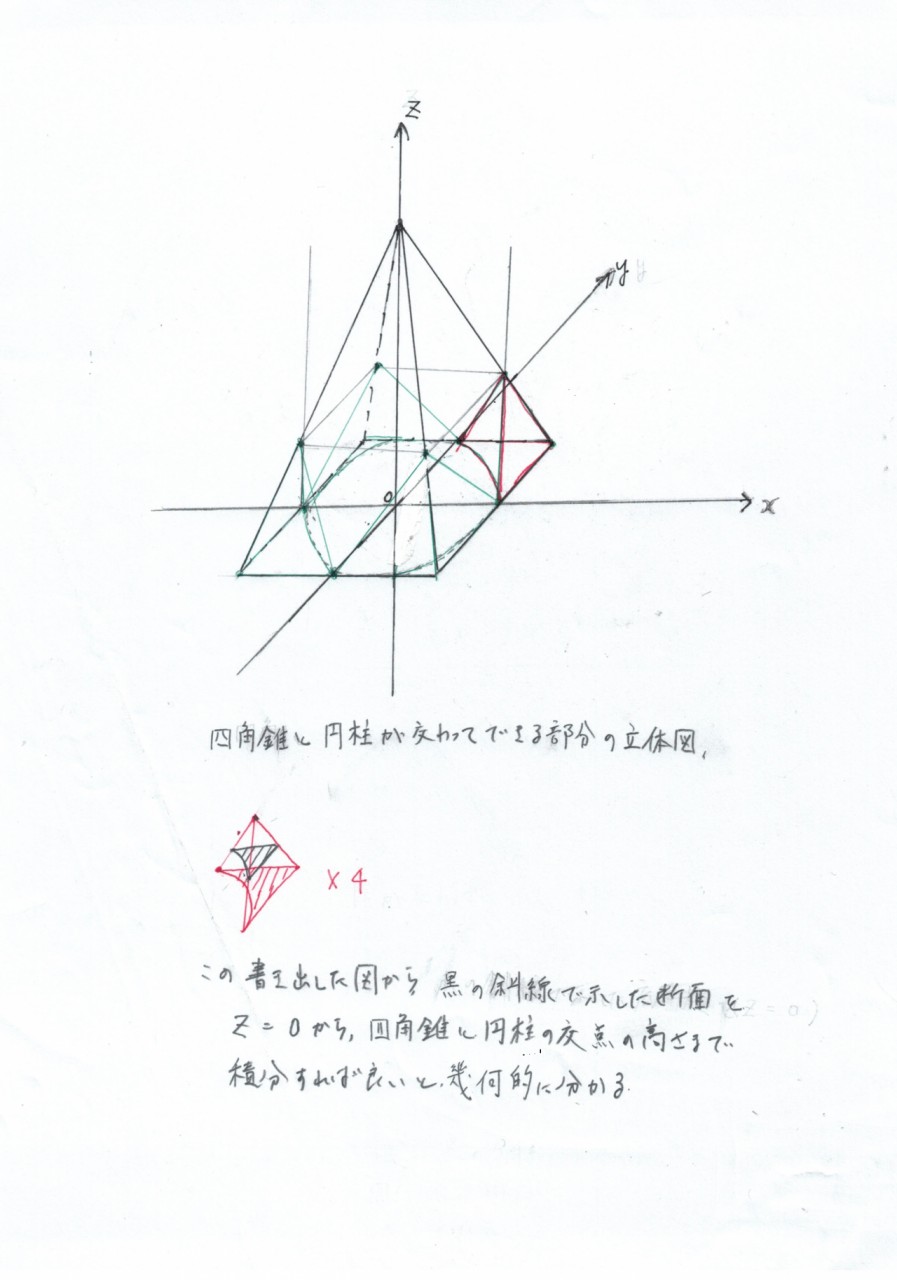
② どの平面に崩すか?
問題文よりx^2+y^2>=1
四角錐の高さ(Z方向)を考え
0<=z<=3 の範囲で
x^2+y^2>=1
を満たすことが必要なので
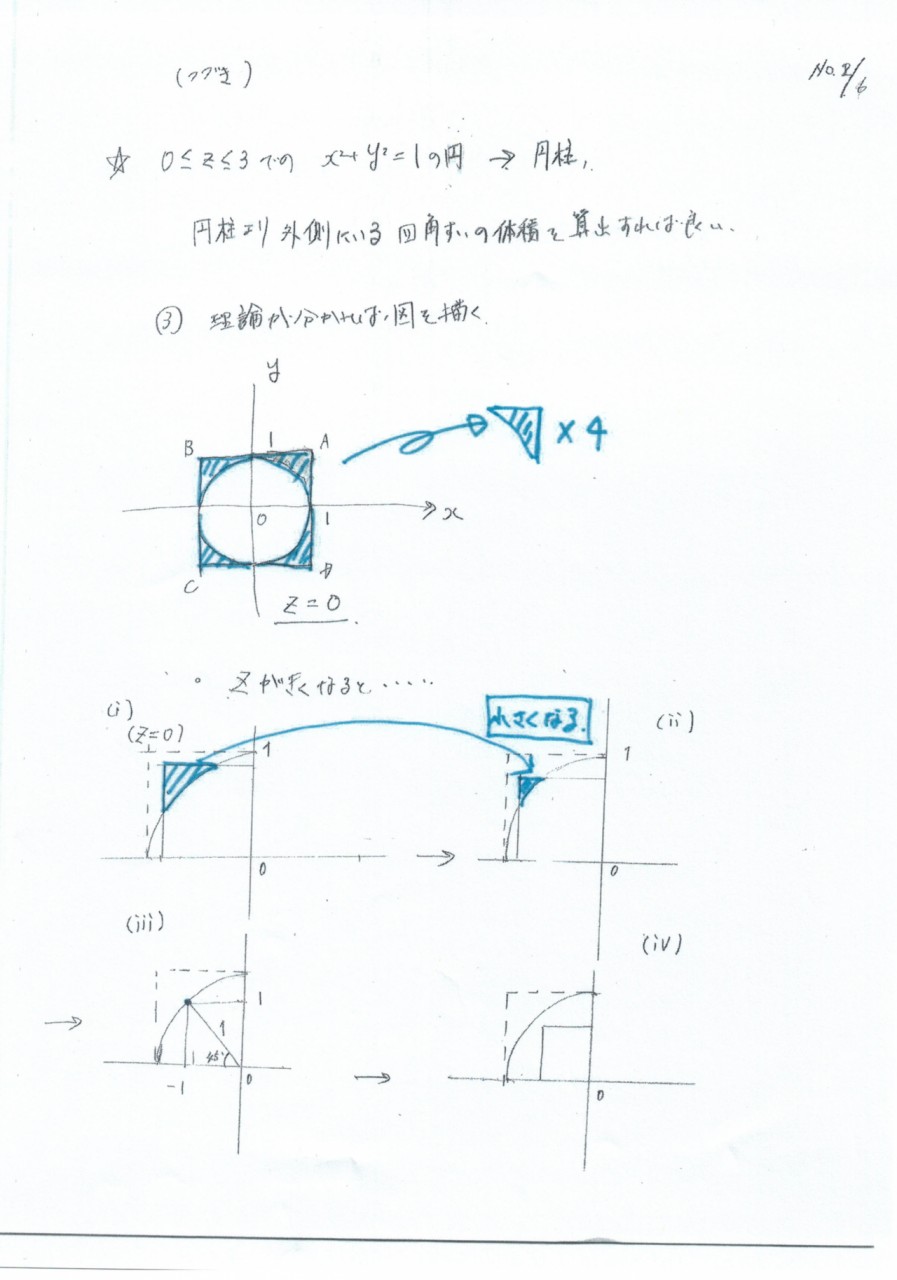
図示したように、zの値を変えながら
xyに平行な平面(断面)で見れば
積分するために必要な断面がどう変化するかが分かる
➤ 求めたい断面は大きさが異なる
(zを大きくすると、面積は小さくなる)だけで
形は常に同じ(相似)であることが分かる。
(図の青の部分)
あとは、(ⅲ)の状態になる時のzの値を求めれば積分範囲が分かる。

辺の長さや角度を求めたいなら
求めたい辺や角を含む平面で考える
これは頭に入れておいてください。
重要なことです。
断面とそれに垂直な積分範囲が分かれば後は計算するだけです。
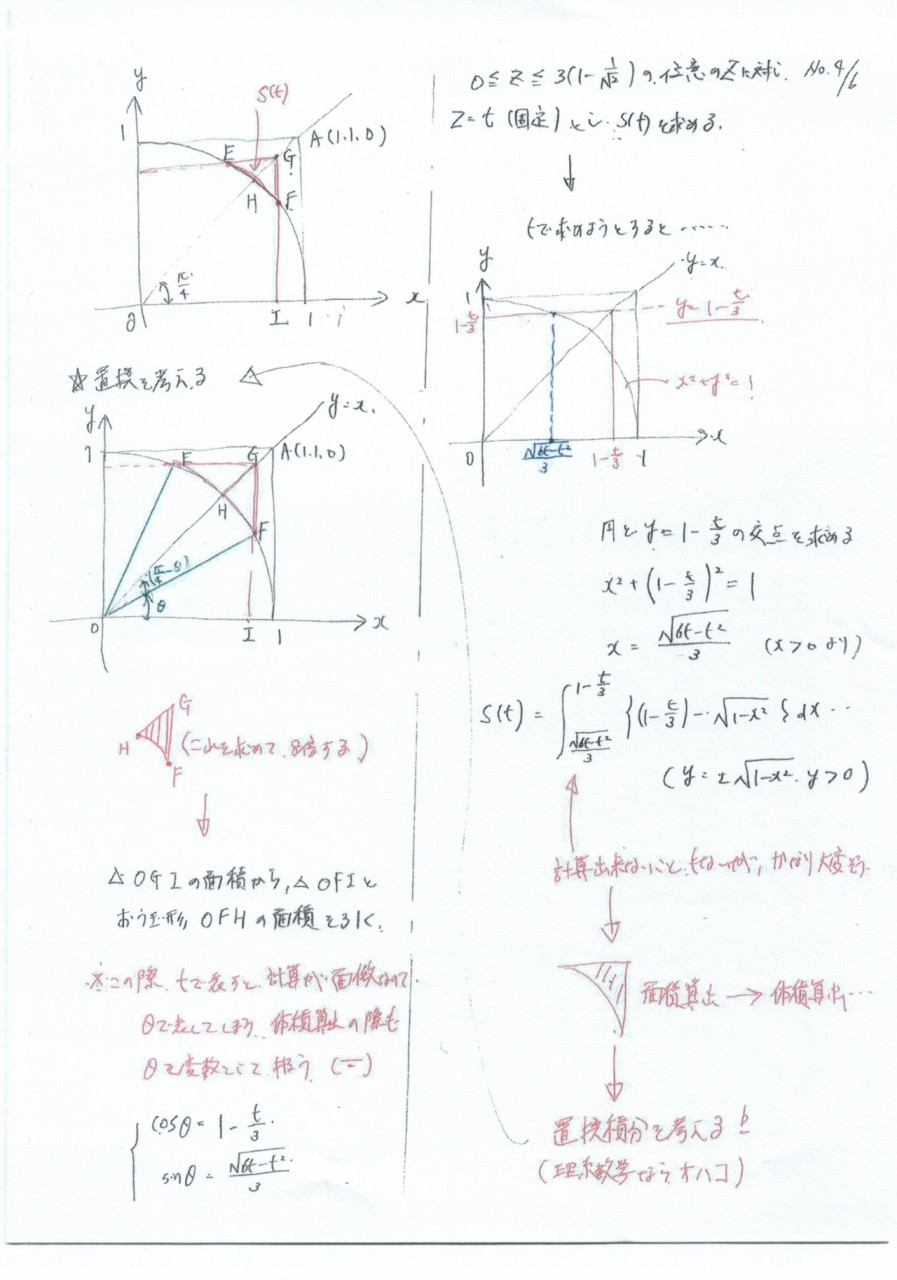


計算に関しては今回は触れません。
コツを言えば、立式した時点で
合成関数の知識が即座に出てくるかどうかです。
重要なことは
空間図形を処理するために、
必要なノウハウを理解すること
皆さんの偏差値アップに貢献できれば幸いです。
かなり昔ですが、東大理類の問題です。
(実際に指導した際にこうした解説資料を用いることもありました。)
(※ 資料は当時手書きで私が解いて作ったものです。読みにくかったらごめんなさい🙇)
まとめ
空間図形に限らず
・自分の弱点を知る
・どごを重点的に勉強すれば解けるようになるか
・克服するのにどの程度の時間を要するのか
・解法プロセスを理解してもらえるまで根気強く指導する
武田塾岡山西口校は
こうした事を細かく分析した上で
塾生個々に合った最適解を提供しています。
~大学受験塾・予備校なら~
【武田塾岡山西口校】
岡山市北区駅元町30-13横田ビル3F
(岡山駅西口から徒歩2分)
【tel】086-250-3375
【e-mail】okayama@takeda.tv
〈月~土曜日〉
【自習室利用可能時間】13:00~22:00
【電話受付対応時間】 13:00~22:00
〈日曜日〉
休校















