直前確認!覚えておいた方がいい公式、導くことができた方がいい公式集
このブログをご覧の皆さん、こんにちは。
武田塾大泉学園校の講師Oです。
今回はタイトルに書いてある通り、直前に覚えておくと得する公式集を紹介します。
センター試験に役立つものも紹介する予定ですが、主に二次試験などの記述式で役に立つものを取り扱っていこうと思います。
難易度順に分けていくので、自分に適切なレベルのものを吸収するのもいいし、さらに上のレベルを目指す人は別の記事も総なめしていってください。
それでは始めます。

レベル1 センター試験~日大レベル
まず紹介する公式はこちらです。
~絶対値の性質~
非常に基本的なことではありますが、この性質が絶対値を含むすべての問題で重要になってくることは、問題をたくさん解いてきた受験生の皆さんならご理解いただけるはずです。
特に、②は不等式の問題で利用したり、後に扱う三角不等式や相加相乗平均を利用する時に利用するので、ぜひ覚えておきましょう。
~覚えておきたい公式その2:二次関数、二次不等式編~
数学Ⅰで扱う二次関数、二次不等式ですが、これらで最も重要なものは解の公式です。
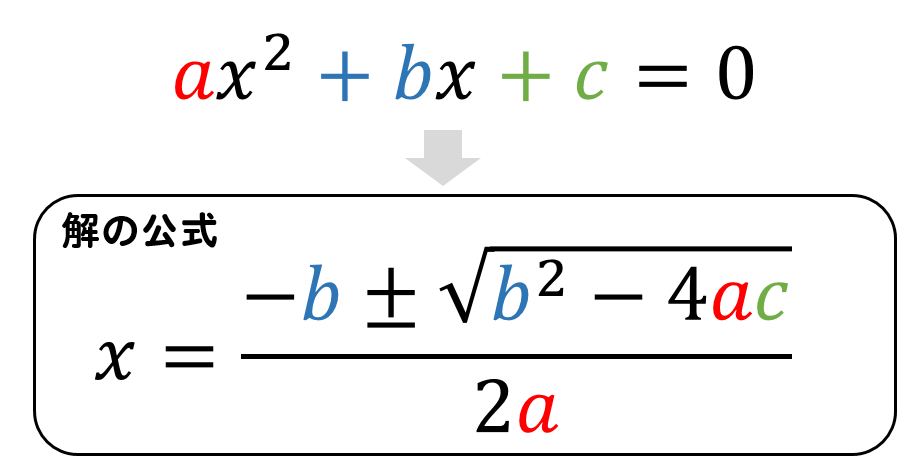
これが大事なのは言うまでもありませんが、重要なのはここからで、この解の形を利用した公式を紹介します。
ここから先は二つの解をp,qで表します。(p<q)
その1
p+q=-b/a
と表されます。
あまりこの公式の有用性がわからない人は多いと思いますが、重要なのは解どうしを足したら根号の部分が消えてくれるということです。ここから,2解がわかっているときにそこから二次方程式を決定する際、役立てることが可能になります。
また、絶対値をつけて
|q-p|と取り扱うことによって、ある二次関数をx軸で切り取った長さがわかります。
~その2;理解しておくべき判別式の中身~
皆さんがご用達の判別式、D=b^2-4ac ですが、なぜこれが0との大小関係においてその二次関数の解が決まるかどうかを説明できますか?
その理由は、先ほど説明した解の公式にあります。
一度上までスクロールして見ていただくと、Dはこの解の公式の根号の中身であることがわかります。
例えば、D>0だった場合は根号の中身は実数で表すことができ、解を二つに表すことができます。
次に、D=0だった場合は解はx=-b/2aとなるため、解が二つになります
最後にD<0のときは根号の中身が虚数になるため、解なし(または虚数解が二つ)と表現します。
いかがだったでしょうか。
判別式Dはいたるところで使用するので、きちんとその仕組みを理解するようにしましょう。
その3 図形と計量 公式は使いどころまでしっかり押さえよう!
ここの単元で重要になってくるのは、当然余弦定理や正弦定理になってきます。
しかし、それをただ暗記しているだけでは意味がありません。
ここで重要になるのは、問題を見た際に「これは正弦(余弦)定理だ!」と気付けることが大事です。
それでは、主な使い分けのやり方について記していこうと思います。
~パターン1~
二つの辺と、それに対応する角が分かっている場合。
→これは正弦定理になります。
~パターン2~
3つの辺が分かっているor二つの辺とその間の角が分かっている場合
→これは余弦定理になります。
このように、わかっている角と辺の位置によって定理を即決で使い分けれるようになると、大幅に計算スピードを速くすることが出来たり、正しい方針で進められることができるので、是非覚えておきましょう。
その4 データの分析
センター試験で重要な単元といったらここでしょう。
何故なら、対策すればするほど点数が伸びやすいからです。
データの分析で高得点を目指すには、定義をしっかりと覚えていくことが重要なので、下に重要な公式一覧を載せておきます。
分散の公式 言い換え
(Sx)^2=(x^2の平均値)-(xの平均値)^2
と言い換えることができます。これは、与えられているデータが少なく、平均値が最初から出されている問題に対して非常に有効です。証明もできるようにしておきましょう。
~その2~ センター試験に毎回で47都道府県のデータ
共通テスト対策に勤しむ皆さんには既におわかりだと思いますが、センター試験のデータの分析には毎回47都道府県のデータのことで溢れています。
ここで皆さんに覚えておいてもらいたいことはこのデータの中央値です。
47は奇数なので、24番目のデータが中央値になります。皆さん、この数字はヒストグラムや箱ひげ図を確定する時に最も役立つといっても過言でないほど重要な数値なので、よく覚えておきましょう。
終わりに
いかがだったでしょうか。今回紹介した公式やその使い方は、様々な場面に応用できるのでぜひ使ってみてください。それでは!












