数学ⅠAの特徴や難易度、勉強のコツを紹介

こんにちは。
授業をしないでおなじみの武田塾小田原校です!
今回から、数学ⅠA・ⅡB・Ⅲの各単元について、特徴・難易度・勉強のコツを紹介していきます。
苦手単元がある方は、是非このブログに書かれていることを参考にしてみてください。
今回は数学ⅠAの特徴・難易度・勉強のコツを紹介していきます!
数学Ⅰの特徴・難易度・勉強法
数学Ⅰで学ぶ単元
|
・数と式 ・図形と計量 ・二次関数 ・データの分析 |
「数と式」の勉強法・特徴

数と式の単元では、まずは数とはなんなのかについての定義から学習が始まります。
整数、実数、虚数、正の数、負の数、素数などについて、正しくその定義を理解することがこの単元のポイントとなります。
ここを疎かにすると、これから先で学んでいく高校範囲の学習の根幹が揺らいでしまうので気を付けましょう。
概念を理解するだけなので、難易度はそれほど高くない分野と言えます。
集合という概念について学習する
また、集合という概念についても学習しますが、この考え方は大学に進学した際により詳細に学習する分野なので、大学進学を考えている場合は、丁寧に内容を押さえておく必要があります。
受験に限った話をすれば、受験生の多くは、命題の真偽を答える問題や、必要条件・十分条件について考える問題に苦戦する傾向があります。
共通テストでも出題されやすいところなので、対策には時間をかけた方が良いでしょう。
式の分野では、因数分解や不等式の解法を学ぶ
式の分野では、因数分解や不等式の解法を学びます。
因数分解は、y=0の時の関数の解を求める際や、整数問題で条件に合致する整数を選び出していく際に重要となる考え方です。
中学生でも因数分解は習いますが、高校範囲ではそれよりは高度なものも出てきますので、苦手としないためにも、たくさん計算練習を行うと良いでしょう
特に、累乗が関係してくる因数分解の中には、公式のように暗記しないといけないものがいくつか存在しますので、教科書に載っているものは完璧に覚えておく必要があると思ってください。
図形と計量

図形と計量の分野では、三角比について学習します。
数と式の分野が中学数学の延長のように感じられるのに対し、この分野ではサインやコサインといった高校で初登場となる数字が出てくるので、ここでつまずいてしまう学生は多いかもしれません。
それを防ぐためには、まずはサイン・コサイン・タンジェントがそれぞれどのようにして求められる値なのかを正しく理解しておくと良いです。
また、有名角に関する三角比の値は、瞬時に答えられるようにすることが、今後の数学の学習においては必須な事項となりますので、2種類の三角定規のことを思い出しながら理解を深めてください。
正弦定理や余弦定理に関しては、単に公式を暗記しようとしても実際に使える能力にはならないので、それらが関係する演習問題をたくさん解いて、どのようなパターンの時にその考え方を用いれば良いかを見抜けるようになることを目標にしましょう。
特に余弦定理に関しては、数学ⅡBや数学Ⅲとの融合問題で必要になる場面が多いので、余裕があれば、そのような応用的な問題の学習も視野に入れつつ学習を進められると良いです
二次関数
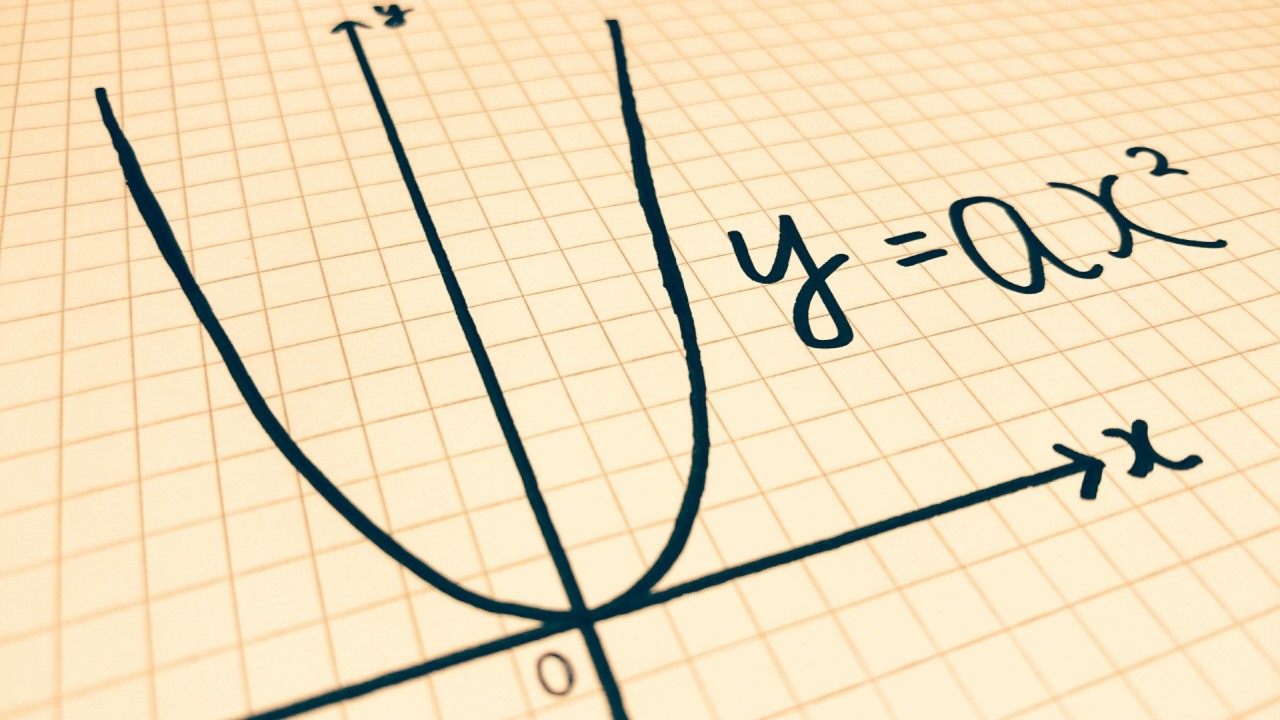
中学校でも二次関数について学習しますが、その多くは頂点が原点に位置するものです。
それに対して、数学Ⅰの範囲の二次関数は、頂点の位置が座標の様々な部分に存在するものとなります。
また、中学範囲ではグラフは基本的には下に凸ですが、数学Ⅰでは上に凸の関数も登場します。
これらにより、x軸との共有点の個数を考えたり、ある区間における最大値や最小値を求めさせたりする問題が出題されるようになります。
二次関数に限らず、グラフを操作する問題で重要なのは、式だけを見て計算を進めようとしないことです。
計算の際には必ずグラフを描く習慣をつけて、視覚的に問題ごとに与えられた条件を理解できるようにする工夫が重要です。
この二次関数の分野で正しくグラフが描けるようになると、数学Ⅱの指数関数や対数関数、数学Ⅲの複数の関数が絡みあった関数についても、グラフの概形を意識しやすくなり、問題を解くことがぐっと容易になります。
また、積分の範囲では面積を求める問題が多数出題されますが、この時にも、正しくグラフを描くことができていると、正答に近づきやすくなります。
慣れないうちはうまくグラフを描けないかもしれませんが、何度も描いているうちに、自分の分かりやすい形式で描けるようになりますので、普段から意識するようにしてみてください。
データの分析

データの分析は、ほぼ共通テストのために勉強する分野で、二次試験でこれがメインとして出題されるということはほとんどないと思われます。
大学に進学する場合は、理系・文系問わず、「統計」という考え方が重要になってきますが、その基盤となるのが、このデータの分析だと思ってもらうと良いです。
テキストに書かれている事項を覚えていくことが学習の基本となるため、計算練習をたくさん行うような他の分野とはやや異なる学習法が必要になります。
数学A
数学Aで学ぶ単元
|
・場合の数と確率 ・整数の性質 ・図形の性質 |
場合の数と確率

中学校でも確率に関してはごく簡単な部分を勉強しますが、高校範囲では、そこからさらに進んだ内容を学習します。
入試問題においても場合の数や確率は頻出なので、数学ⅠAに属するからといって疎かにはできないことを覚えておいてください。
場合の数や確率について考える際に重要となるのは、数え漏れのないようにすることを普段から意識することです。
特に確率に関しては、特定の条件を満たす確率の和は1になることを知っておくと、問題を解く際の大きなヒントになるだけでなく、検算をすることも容易になります。
それ以外では、P(並べる)とC(選ぶ)の違いを正しく理解することが重要と言えます。
確率の問題が苦手な学生は、これらの定義を疎かにしているか、もしくは正しく理解していないということが多いので、自分がそれに該当する場合は、教科書の対応するページを丁寧に読み直す作業をすると良いです。
一見複雑に見えるような問題でも、少しずつ紐解いていくと、基本的な確率の考え方を寄せ集めたものであることがほとんどなので、それを見抜けるようになるまで問題演習を重ねることが、この分野を得意にする鍵となります。
整数の性質

整数は、おそらく受験数学の中で、一番難問が出題されやすい分野になります。
整数以外のほとんどの分野は、教科書に載っているような考え方をうまく当てはめることができれば答えに辿り着けるため、たくさん問題演習を行うことで、ある程度は対策することができます。
それに対して整数は、新規の発想力や思考力をダイレクトに問うような問題が多く、なかなか一筋縄では解くことができません。
大学を例に挙げれば、京都大学は整数に関する証明問題を出題することが有名で、高度な論述の力を持ち合わせていないと、なかなか高得点を取ることは難しい構成となっています。
普段の学習において意識すべきことは、解答に必要となる最低限の知識は完璧にした上で、未知の問題に時間をかけて取り組む練習をすることです。
数学においては、難問に時間をかけて取り組む機会が多ければ多いほど、自分の中の経験値が高まって、初見問題にも食らいつけるようになっていきます。
整数の問題では特に、分からない問題があってもすぐに答えは見ずに、最低でも1日程度は思考する時間を設けてみると良い練習になるでしょう。
図形の性質

図形の性質の範囲では、主に三角形の性質や円の性質について学習します。
二次試験でこれらがメインで出題されることは少ないですが、図形に関するセンスを養っておくと、本来ならば積分や微分によって数値を求めないといけない問題を、幾何的なアプローチで解くことができて、大幅に解答時間の短縮につなげられる可能性もあるので、余裕がある学生は、幾何に関する知識を蓄えておけると良いかもしれません。
特に、特定の直線に円が接している条件から発展して、最終的に不等式の示す範囲の面積を求めさせる問題などでは、円の性質を最大限に利用することが、解答へのスムーズな道のりになることが多いです。
単元としては簡素なものですが、その他の分野との融合問題のことを考えると、疎かにはできない単元だと言えます。
【まとめ】数学ⅠAで学んだことを基盤として、これから先の数学が広がっていく

数学ⅠAは基本的には高校1年生が学習するものという位置づけなので、極めて難易度が高い概念が紹介されるということはないです。
しかしながら、丁寧に学習を進めておくと、その後の勉強の役に立ったり、融合問題を解く際の別解に利用できたりと、なかなか奥が深い分野だと言えます。
学習を進める際は、共通テストのことを意識することも大切ですが、ここで学習したことを基盤として、これから先の数学が広がっていくということを常に頭に入れておくと良いでしょう。
Youtubeも参考に!数学の勉強法(全部入りVer.)|教科別勉強法
↓勉強の悩みを無料で相談したい方はこちら↓
3種類の申し込み方法からお選びください
|
①「無料受験相談」より、必要事項を記入の上、お送りください。
②「友だち追加」よりLINEをご登録後、受験相談希望の旨、メッセージをお送りください。
③ 校舎へ直接お電話頂き、受験相談希望の旨をお伝えください。 TEL:0465-22-3911 (受付時間10:00-22:00) |
◆武田塾小田原校◆
小田原駅近辺で大学受験の塾・予備校をお探しなら武田塾小田原校
| TEL | 0465-22-3911 |
| odawara@takeda.tv | |
| 住所 | 神奈川県小田原市栄町2-8-37-3F |
| アクセス | JR・小田急小田原駅東口より徒歩3分 |

















