こんにちは！武田塾西宮北口校で教務をしています池上です。
連載企画として勉強法についてお伝えしている「スライムの勉強道場」第５回！
今回は、おやおや、前回と前々回とタイトルが同じだな？？「勉強でつまづくとき」についてさらに深掘りしていこうと思います！
はじめましての方へ
少し自己紹介をしますね。
最近は受験生の気持ちになろうと思って家で勉強をしているのですが、
朝は非常に眠くなりますね。
昼も眠いです。
僕はもともと夜型で、高校生の頃から朝起きるのが苦手でした。
基本的に朝勉強したことはありません。
模試や入試の日だけは頑張って朝行きましたが・・・。
やっぱり人によって朝と夜どっちのほうが集中しやすいかはあると思います。
モンスターも同じですね。
だから昼と夜では出現するスライムの種類も違うんですね。
＊昼のスライム
あと詳しくは前のブログに書いているので見てみてね！
そんな私ですが、武田塾の生徒を見ていて、もっとこうしたらいいのに、と思うことがたくさんあります。
もっとこう考えたらいいのに。
もっとこうすればできるのに。
そんな風に日々感じたことを何かの形で残しておきたく、この度ブログで書いております。
ぜひ塾生にも読んでほしい内容です。
塾生以外のみんなも、勉強方法とスライムについて気になることがあったらぜひ西宮北口校まで話を聞きに来てね！
＊あくまで私個人の考えなので、武田塾での指導内容と完全には一致しない部分もありますが、本質は似ていると思います。
どうか受験勉強に悩むみなさんの参考になれば幸いです。
ただし、私はあまり甘いことは言わないので、ダメージを受ける覚悟をして読んでください(笑)
ということで、今回は第５弾、勉強でつまずくときの続きです！
具体的には、「理解できない」「参考書が合わない」「問題が解けない」「時間がかかる」ときについてです。
勉強でつまずくとき
つまずくときの状態の一つとして、そもそも理解できない場合がありましたね。
「理解できない」
理解できないときは、主に以下の２パターンのどちらかであるという話をしました。
・内容が難しすぎる
・適切な読み方ができていない
今回は後者の「適切な読み方ができていない」場合の続きです。
適切な読み方ができていない場合
この場合に考えてほしいこととして、前回は
・言葉の意味をわかっているか
・図で表せるものは描いているか
・他のものに置き換えて考えてみる
について紹介しました。
今回はさらに、
・その説明の目的は何なのかを考える
・細かく分解する
についてです。
●「その説明の目的は何なのかを考える」
特に問題の解説などのケースであります。
なぜこの式（式変形も含めて）が出てきたのかがわからない、
この一文が言っていることがわからないという場合です。
＊何を言っているのか理解できてない人
ここでまずやってほしいのは、以前に紹介した、
言葉の意味を分かっているか、図で描けるものは描いているか、他のものに置き換えて考えているか、
などがありますが、それでもわからないこともあります。
このようなときは、今自分がわからないその部分が、
「解説全体の中のどの位置にあるのか」を考えることで理解しやすくなる場合があります。
例えば、数学の例を出してみます。
「整数nによって変化する確率P(n)の最大値を求めよ」という問題に対して、
解答ではP(n+1)/P(n)の式変形をして、次のようなことをします。
P(n+1)/P(n) = (n^2-n+6)/(n^2+1) = (n^2+1-n+5)/(n^2+1) = 1 - (n-5)/(n^2+1)
＊n^2はnの2乗という意味です。なお、数値は適当に作っています
この式変形を見た時点で「なぜこんな変形をするのか理解できない」という人がいます。
でもその後の部分を見たら意味は分かります。
解説の続きを書いてみましょう。
この形にすることで、P(n+1)/P(n) は
・nが5のとき、1になり
・nが1~4のとき、1より大きく
・nが6以上のとき、1より小さく
なることが分かります。
つまり、
・nが5のとき、P(n+1)/P(n) = 1
・nが1~4のとき、P(n+1)/P(n) > 1
・nが6以上のとき、P(n+1)/P(n) < 1
すると、
・nが5のとき、P(n+1) = P(n)
・nが1~4のとき、P(n+1) > P(n)
・nが6以上のとき、P(n+1) < P(n)
よって、P(n)は、nが1から順に増えていくとき、nが5になるまでは大きくなっていくが、
6よりも大きくなると徐々に小さくなっていきます。（n=5とn=6では同じですが）
したがってP(n)はn=5または6のときに最大値をとるということが分かります。
ではここで、先程わからなかった意味を考えてみましょう。
式変形によって1が分離されましたが、それは
P(n)とP(n+1)の大小関係を分かりやすくするためだったんですね。
それもそうです。
P(n)がnの値の変化に伴ってどのように変化するのか分からない状況において、
「最大値を求めよ」ときたのですから、おそらくP(n)はだんだん大きくなってどこからか小さくなっていくはずです。
（でなければ最大値が存在しない）
最大値を求めるには、
P(n+1)/P(n)の値が1より大きくなったり小さくなったりする場所を探せばいいんですね。
途中で行われた式変形の時点では意味が分かりませんでしたが、
その後の処理を見れば、なぜそれを行ったのかは理解することができました。
このように、
「その問題では何を問われているのか」
「それを求めるためには何をしたらいいのか」
「わからない部分の前後では何が書かれているか」
という流れを確認することで、わからない部分では何が書かれているのかを、理解または予測することができるのです。
＊雨が降って蒸発してまた雨が降って・・・という流れ
その予測があるのとないのとでは、内容を読んだ時に理解できる度合いが違います。
今回のケースでも、分かった上で読んでみればなんてことはないはずです。
特に数学は、
「何をやっているのか（理屈）」
「なぜそれをやっているのか（理由）」
が分かっていれば、ほとんど分からないことはなくなります。
あとは細かい計算が合っているかとか、そういう部分だけです。
今回と違う場合ですが、多くの文章解説を読むときなどにも、
その中で自分がほしい情報が何なのかがあらかじめ分かっていると見つけるのが容易になり、理解しやすくなります。
人ごみの中で知り合いを探すとき、
その人がどんな色の服を着て、どんなかばんを持っているのかが分かっていれば、
きっとそれらにも注目して探すはずです。
そうするとただ顔を知っているだけの人を探すよりも見つけやすいですよね。
それと同じです。
＊人を探す人。サイズ的に進撃の巨人ですね
ただしこれは他の部分をある程度理解できる状態であることと、
そこから論理的に考えて予測する力があることが必要なので、難しいとは思います。
しかし、これは独学には必須な力です。
また、試験本番で英語長文中のわからない単語を予測する場合などにも使えますので、ぜひ一度やってみてください。
●「細かく分解する」
言葉の意味が理解できないときの対処と似ていますが、これは特に数学の式変形でよくあります。
ここからここの式変形の理屈が分からない、というような場合に有効です。
前項の、その説明の目的を考えることで解決する場合もありますが、
前後とか関係なくその部分の変形だけがよくわからない、みたいな場合です。
そういうときは、「一つ一つの数字や文字が何を表しているのか」や、
「変形前と変形後で違っている部分はどこか」を考えます。
＊この二人の違いを探してみましょう。右が大学の頃で左が社会人になってから
まずその区別をするだけでも、何が変わったのかは分かります。
次にその変化した部分について、もう少し具体的に何が変わったのかを考えます。
このとき、わりと根気よく一つずつ調べる必要があります。
例えば、
∑のk=0,1,2,3,・・・nだったのが、∑のk=0,1,2,3,・・・n+1になっているとか、
細かい変化があったりするので、しっかり確認しましょう。
頭の中で処理できないときは、できるだけ全部書き出すといいです。
他にもつまずきやすい変形としては、n!と(n+1)!の変形があります。
（実際これに関わる問題で、質問に来る生徒がちょくちょくいます）
例えば次の式を見て、最初は？となりませんか？
n!=(n+1)!/(n+1)
でも、先ほどと同様に一つずつ書き出してみるとなんてことはありません。
こういう変形を解説で細かく書き出すことはまずしていないので、自分でしっかり書き出して確認しましょう。
この式についてもあえて説明はしないので、もしぱっと見てわからない場合は一度書いてみてください。
さて、ここで「理解できない」場合の対処法はいったん終わりです。
次は、「参考書があわない」場合について。
「参考書があわない」
ちょこちょこ聞きますね。
これについてはかなり賛否両論あるかもしれませんが、私の個人的な考えを書きます。
えっとですね・・・まずひとつ言いたいのは、
参考書のせいにばかりしている人は伸びません。
と言いたいのですが、合わないものがあるのも分かります。
ただし、なんとなく合わないではなく、合わない理由は明確にすべきかと思います。
私が思う合わない理由は
・レベルがあっていない
・レイアウトやデザインがあまりに気に食わない
・考え方が自分のものとずれすぎている
あたりかと思います。
●「レベルが合っていない」とき
これは参考書をすぐに変えましょう。
難しすぎるものを読んでも頭に入りません。
めちゃめちゃ時間をかければできなくはないと思いますが、非効率的です。
簡単なものから始めましょう。
●「レイアウトなどが気に食わない」とき
嫌なら変えても良いかもしれません。
しかし、変えても解決することは多くないように思います。
というのも、そういう人は自分の成績が上がらないのを参考書のせいにしていることが多いからです。
本番の入試問題のレイアウトが気に食わなったらどうするのでしょうか。
もちろん普段の学習は好みのものでやるに越したことはないかもしれません。
しかしそれを理由にいつまでも勉強ができないと言っている人は、受験に向いていません。
＊こういう参考書ならきっと読めますね
塾でないと勉強できないと言っている人も同様です。
家の環境によっては、家でできないのはまだわかりますが、その気になれば
図書館でもどこでも場所は見つけられるはずです。
その程度の意思で受験に勝つことはできません。
自分でなんとか練習場所を確保したり、一生懸命取り組んだりせずに
試合に勝てるスポーツ選手などいないでしょう。
厳しいことを言っているかとは思いますが、本当のことです。
少なくとも関関同立以上の難関大学を目指すならば、勉強の前に心構えから変えることをお勧めします。
●「考え方が自分とずれている」とき
例えば国語の参考書において、問題の解き方などが書かれていますが、
特に国語という科目は感覚で読んで解いている人が多いと思います。
すると、「なんかこのやり方はあわないな」と思って我流を貫く人がいます。
実際、それでかなりできる人がいるのも事実でしょう。
しかし、本当に勉強ができる人は、参考書のやり方も取り入れることができると思います。
自分のやり方では通用しない場合もあります。
そういうときのために他のやり方や考え方を知っておくことも大事です。
＊オウムは真似しますよね。学ぶ＝マネぶです。これは閑古鳥
それに、これは余談ですが、
そもそも自分のやり方がうまくいかないときは矯正せざるを得ません。
自分のクセややり方を変えることは、非常にエネルギーを使います。
例えるなら、いつも右手で持っている箸を左手で持つようにするくらいのエネルギーです。
容易ではないでしょう。
でも、そういうのを当たり前の状態になるまでやりこまなければ、自分の壁は破れません。
勉強でつまっているときにアドバイスされたことを、中途半端にやっただけで
「自分に合わない」とか「できない」とかほざいている人はいい加減にしましょう。
スポーツの型を習ったときにすぐにできましたか？
よほど運動神経のいい人でない限りは苦労したはずです。
少なくともそれと同じレベルでのしんどさはあると考えましょう。
甘ったれる前に一度全力でやってください。
「問題が解けない」
これは、問題集をやるときによく陥ります。
というか、問題がすらすら解けるなら、その問題集をやる必要はありません。
つまずいて当然と思いましょう。
ただし、どういう部分でつまずいたかを考えることが大切です。
解けなかった場合の原因は大きく二つです。
・知らない知識が使われていた
・知っている知識で解けるのにそれを使う判断ができなかった、または使ったけど間違えた
●知らない知識が使われていた
これは間違えて当然です。
これから先も自分が知らないやり方などいくらでも出てきます。
入試までにそういうやり方を少しでもできるようにしていくことが勉強です。
そこでできるようにしましょう。
ただし、解答の中で、自分が知っている知識で解ける部分まではたどり着けていたかはチェックしてください。
●知っている知識で解けるのにそれを使う判断ができなかった、または使ったけど間違えた
これはどの教科でもありますが、数学などが顕著かと思います。
例えば「あっ、ここで解と係数の関係使うのか～」というのは私も昔よくありました。
数学の場合は特に、問題の解き方がいくつか存在するときがあるので、難しいですよね。
そんなとき、必ず気にしてほしいのは、「解と係数の関係（その知識）」をなぜここで使ったのか、ということです。
（＊解と係数の関係 ：2次方程式ax^2+bx+c=0の２つの解がα、βのとき、 α＋β＝-b/a , αβ＝c/a ）
例えば2次方程式では、解の公式で二つの解を求めてからα＋βを求めることもできます。
ただ、この二つの値をそれぞれ出してから計算をすると、手間がかかります。
解と係数の関係を使うと、非常に楽に計算ができます。
（例えば3x^2+4x-1=0などで実際に確かめてみてください。）
そうすると短時間で計算ができ、かつ計算ミスも減らすことができます。
だから使うのです。
（他の理由で使うときもあるでしょうが）
これを、何も考えずに解の公式を使って計算してしまうというのがよくない状態です。
最初のうちは仕方ないですが、繰り返すにつれて、
必ず「なぜその計算を行うのか」という理由を考えるようにしましょう。
いま考えている計算の前後で何をしているのかを見れば、
その計算の理由はわります。（すでに書きましたね）
さらにはそれを解答全体へ広げて、この解答は最初から最後までで何をしているのかという流れを理解しましょう。
そうすれば、どういうときにどの公式や定理を使えばいいのかは判断できるようになります。
そうすると、次の段階として、
「使うことはできたけど、間違えた」ということが起こりえます。
これは、単なる計算間違いや、前提を忘れていたなどのミスがありますが（対数で、真数条件を忘れていたなど）、
それ以上に意外とよくあるのが、「やってみたら途中から分からなくなった」です。
＊道がわかると思っていたらわからなくなった犬
数学の問題というのは、難しくなればなるほど文字が増えることが多いです。
2次方程式においても、係数が単なる数字のものと、文字で置かれているものとでは難易度が違いますよね。
文字になるととたんに計算ができなかったり、条件を間違えたり、途中から変形ができなくなったりすることがあります。
そこで初めて、「わかったつもりになっていた」ことに気づきます。
数学においては基本的に、全て文字で置かれたとしても正しく計算ができる状態が理想です。
（かなり難しいので、そこまでやらなくてもいいですが）
同じ系統の問題でも、そうやって少し状況が変わったときにどんなことで困るのか、
これは経験を積んで身に着けていくしかありません。
安心してください。これはよほどの天才でない限り全員が通る道です。
初めて学ぶことならば、学校の先生や塾の先生がやっても同じことは普通に起こります。
それを経験したら「ここで気づけてラッキー！」くらいに思いましょう。
それに気づいていかないと、成績は上がりません。
「時間がかかる」
この悩みはきっとみんなあると思います。
考えるべきことは、「いかに効率よくやるか」です。
そのためには、例えば
・勉強のやり方を決める
・勉強したことが身に着いたかのチェック方法をどうするかを決める
・それらを実行して、身につくまでやる
・かかった時間を測る
・修正できるところを考え、次のやり方を決める
といったサイクルを繰り返して、自分にあったやり方を見つける必要があります。
しかしこれは簡単ではありません。
ましてや初めて学ぶことの場合、しばらくはその内容がどんなものかをつかむまでの時間が必要です。
それが分からないとやり方を決められません。
例えば筋トレをやったことのない人が、いきなり筋トレのやり方や計画は決められませんよね。
ある程度それについて知っている人に聞くはずです。
これらを決めるには、最終的な目的地（ゴール）が決まっていて、そこへの道筋をある程度分かってないとできないのです。
だから、最初のうちはやり方を考えるために、まずは量をこなすことも必要です。
つまり結論としては、いきなり効率のいいやり方ばかり考えても意味がない、ということです。
初めからそれを求めるなら、すでにそれをやったことがある人へ聞きましょう。
それが自分にとってベストなやり方とは限りませんが、参考にはなるはずです。
また、もう一つ考えてほしいことがあります。
それは、「効率ばかりを求めるのは危険だ」ということです。
人によって、勉強したことをどれくらい吸収できるかは差がありますし、理解の仕方も違います。
王道のやり方は存在しても、それで全員が同じスピードでできるようにはなりません。
そこで陥ってしまう失敗例として、とにかく参考書を一冊終わらせたけど何も身に着いていないという状態があります。
勉強というのは、身に着かなければ意味がありません。
「1000個の英単語を見たことがある」よりも
「400個の英単語をしっかり覚えている」方が絶対にいいです。
よって、勉強したことが身に着いているかのチェックは非常に重要です。
参考書を読んで満足、ということだけは避けましょう。
そうやって、まずはやったことがきちんとできる状態になっている、というのをクリアしましょう。
それができれば、そこから先はその繰り返しになるので、むしろ勉強の効率は上がっていきます。
＊水力発電は発電効率が高いらしいです。一見ゆっくり回っていますが
「急がば回れ」です。
初めは量も大事ですが、ある程度の量をこなしたら、次は質を上げる。
それから最後までの量をやり切りましょう。
今回はここまでです。
続きはまた次のブログで！！
ちなみに前回の受験勉強ブログはこちら
→【教務池上の勉強ブログ】スライムの勉強道場 vol.④勉強でつまずくとき―その2
武田塾西宮北口校では様々な大学受験のお悩みにお答えします
武田塾西宮北口校では、生徒さんとお父様お母様のために無料受験相談を承っております。
0798-42-7311までお気軽にご相談ください。
ホームページからのお問合せ・受験相談をお申し込みの方は、
からお問い合わせください。
そもそも武田塾とは何ぞや？という方には、こちらの『90秒で分かる武田塾』をチェックしていただけると、よく分かりますよ♪
武田塾のここがスゴイ！
武田塾にはルートというものが存在します。
ルートとは、科目ごとにどの参考書をどういった順番でいつまでに解けばいいかを示したものです。
基本的にはそのルートを元に個別のカリキュラムを設け、
宿題を設定し、毎週確認テストを受け、内容の定着度を確認していきます。
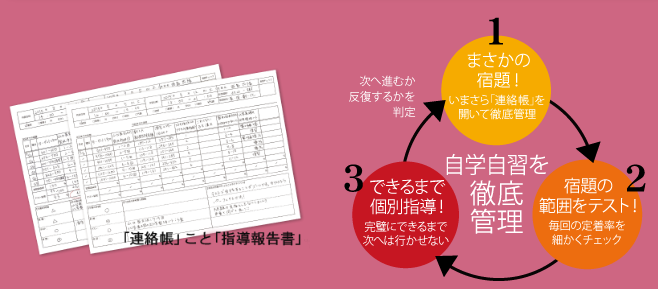
ですので、自分自身の現在のレベルに応じて宿題の設定がされるため
基礎の取りこぼしがなく、進めることができます。
また4日2日の学習ペースで学習を管理していくため
常に一定のペースで学習を進めていくことになります。
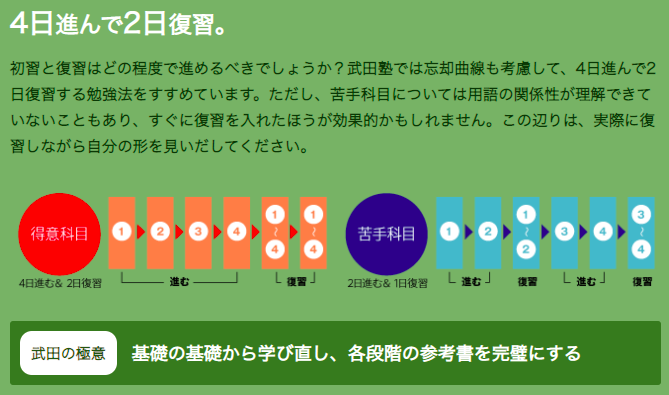
サボったら確認テストの結果でバレてしまいますので
学習習慣をまず身につけていくという点でもお役立ちできます！
なんで授業じゃなくて参考書で勉強するの？
武田塾が授業ではなくて参考書で指導しているのは、授業を受けるだけでは成績は伸びないからです。
いくら分かりやすくて楽しい授業を受けても、
それを何度も復習して完璧に定着させ、試験本番で再現できるようにならなければ志望校に合格することはできないのです。
しかも、大手予備校で神授業をしている先生たちは、その授業のエッセンスを参考書にして販売してくれています。
いわば参考書は神授業を完璧に板書にしたもので、それを読めば理解できるように書かれているのです。
だから、もはや参考書を使わない理由がないのです。
さらに、参考書学習は授業を聞いて勉強するよりも圧倒的に早いです。
例えば英語の文法なら予備校の授業で１年かけて学んでいくことを、参考書学習ならば約２ヶ月で仕上げられます。
また、参考書なら自分が苦手なところについて何回もチェックしたり、付箋を貼ったり耳を付けたりしていつでも見直すことができるので、参考書学習ならば効率的に復習することができるのです。
武田塾では、市販されている参考書を全て調査・分析して、それぞれの参考書のレベルや使い方をまとめています。
そして、志望校合格のために参考書に取り組んでいく順番を示したカリキュラムがルートなのです。
校舎紹介
西宮北口校は2017年1月開校
阪神甲子園校は2019年11月開校
宝塚校は2020年2月開校
岡本校は2020年3月開校
今ならお友達と一緒に入塾すると、
入塾者に図書カード５，０００円分をプレゼント！！
※スタジオコース・期間講習（冬だけタケダ・かけこみタケダ等）・対策講座は対象外です。
※双方が入塾した場合に限ります。受験相談時に記入をお願いします。
西宮市の予備校、塾、個別指導といえば！
〒662-0834
兵庫県西宮市南昭和町2-30山下ビル 2階
(阪急西宮北口駅、徒歩3分)
TEL：0798-42-7311（月〜土 13:00〜22:00）
