こんにちは!武田塾武蔵小山校です。
夏休みが終わり、涼しくなってきました。
夏休みはどのように過ごしましたか?
まだ受験勉強を始めてない人は、まずどこから勉強するのかいまいちわからないと思います。
今回は中学数学の分野を紹介します。
この記事を見てもし何も覚えてないような部分があれば、数学の勉強を中学の範囲の復習からしていきましょう!
中1編
①正の数、負の数
0より大きい数を数字の前にプラス(+)をつけて表し正の数と呼び、0より小さい数を数字の前にマイナス(−)をつけて表し負の数と呼びました。
②文字式
a,b,x,yなどの文字を使った式を文字式と言います。
加減(足し算引き算)では同じ文字同士で計算でき、乗法除法(かけ算わり算)では数同士の乗法除法を考えてそれに文字を掛けます。

③方程式
式の中の文字に特別な値を代入すると成り立つ式のことを方程式と言います。
方程式の解を得るために式変形を行いx=の形にします。
④関数
ともなって変わる2つの数量x、yのうちxの値を決めるとyの値がただ一つに決まる時、yはxの関数であると言います。
中1では主に二つの関数を扱い、y=axのような形を比例、y=a/xのような形を反比例と言います。
⑤平面図形
距離や作図そして円とおうぎ形などの平面図形の基本を扱いました。
例えばおうぎ形の角度をa°、半径をrとするとその弧の長さは2πr×a/360となります。
⑥立体図形
この分野では立体の体積や側面積を扱いました。
体積は主に底面積×高さで出されます。例外として三角錐や円錐がありこれらは底面積×高さ×1/3で体積が求まります。

⑦資料の活用
平均値や中央値、最頻値、範囲などの言葉を習いました。
平均値は全ての値を足したものを度数の合計で割った値、中央値は真ん中の順位の値、最頻値はもっともたくさん出てくる値、範囲は最大値から最小値を引いた値です。
中2編
①式の計算
中1でやった文字式の計算では一つの文字のみの文字式を考えていましたが、中2では二つ以上の文字式を考えます。
②連立方程式
中1でやった方程式では文字が一つ式も一つでした。
中2では文字が複数になり式も複数になりました。
複数の文字がある一つの式を見ても方程式の解は分かりません。
なので他の式を用いて一つの式に一つの文字の状態にして方程式を解きます。いらない文字を消去する方法は加減法と代入法があります。加減法は消したい文字の係数をそれぞれの式で合して、式ごとの足し算引き算を行います。
代入法は必要な文字を別の文字で表しそれを別の式に代入して必要ない文字を消す方法です。

③一次関数
中1では原点を通る直線を扱ってきましたが中2では原点を通らない直線の式や軸と並行な直線も扱います。
軸と並行な直線の式はy=(数)、x=(数)のような形になっていて前者はx軸に平行で後者はy軸に平行になります。
④平行と合同
ここでは平行な時の同位角、錯角の性質や三角形の合同条件を扱います。
三角形の合同条件は3つあります。
(ⅰ)3組の辺がそれぞれ等しい。
(ii)2組の辺とその間の角がそれぞれ等しい。
(iii)1組の辺とその両端の角がそれぞれ等しい。
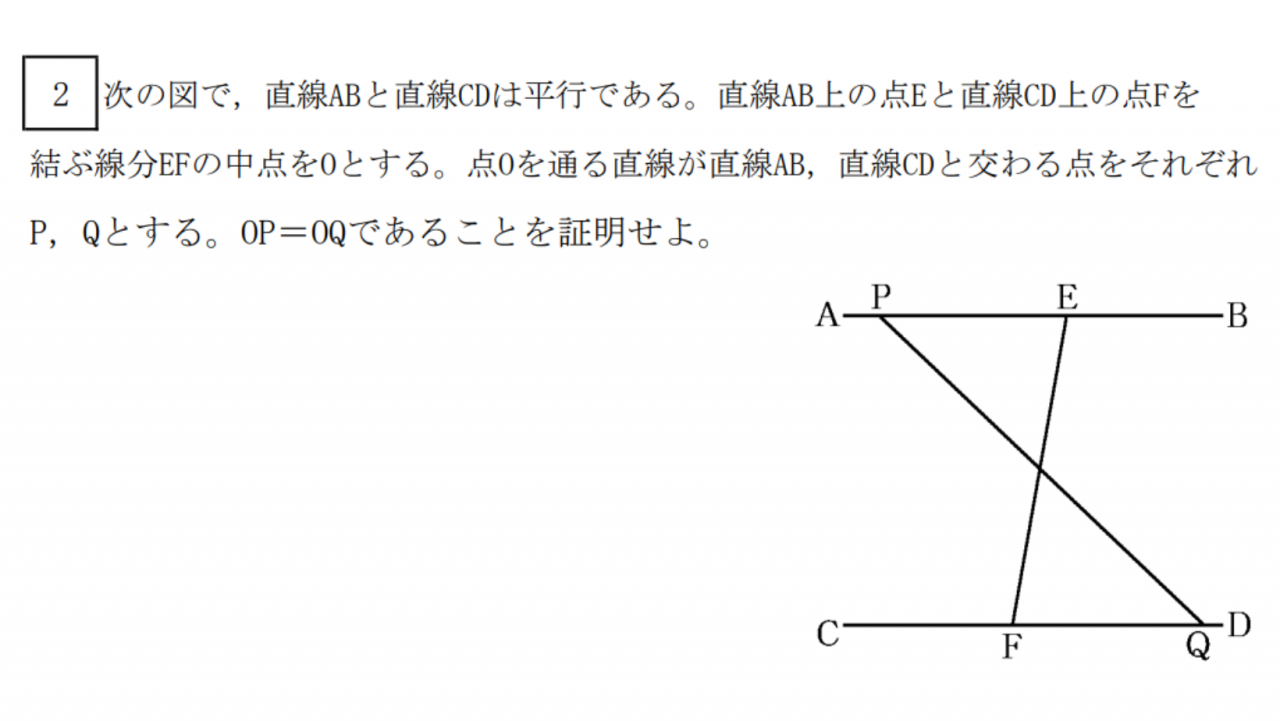
⑤三角形と四角形
二等辺三角形や正三角形、平行四辺形の性質を勉強しました。
⑥確率
確率は求めたい事象の場合の数を全体の場合の数で割ることでもとまる。
基本的な問題は全ての場合を書き出すために表や樹形図を用いたりすることで解ける。

中3編
①展開・因数分解
式のかけ算を計算することを展開といいその逆の操作を因数分解という。
因数分解を解く代表的な方法は共通因数でくくる方法や和と差の積の形を利用する方法などがある。
②平方根
平方根は2乗するするとそのものになるもののことだ。
例えば9の平方根は±3になる、また3の平方根は±√3となる。
±をつけることを忘れないようにしよう。

③二次方程式
二次方程式を解く方法は因数分解を用いる方法と解の公式を用いる方法の二つある。
因数分解を用いる方法は(x-a)(x-b)=0の形に式を変形することで解はa,bとわかるというものだ。
もう一つは解の公式を用いる方法だ。
④関数
中1、中2では直線を学んだ。
中3では放物線を学ぶ。まず放物線の代表的な関数の形はy=ax^2だ。この関数の中でaが正のものは下に膨らんだ形になりaが負のものは上に膨らんだ形になる。
そして放物線と直線の交点を求めたい場合は二つの関数の連立方程式を解くことで求めることができる。
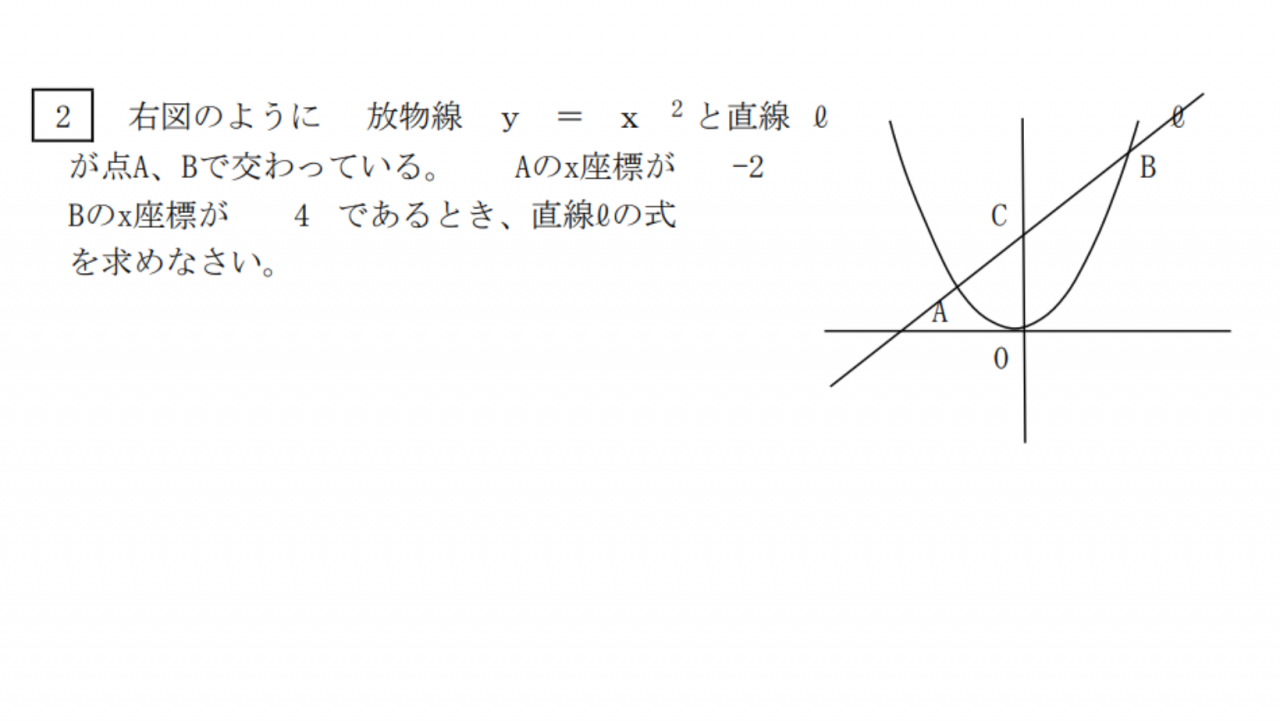
⑤相似
中2で合同を勉強した。合同は形、大きさともに全く同じもののことをさすが相似が形が同じことを指している。
三角形の掃除条件は3つだ。
(i)3組の辺の比が全て等しい
(ii)2組の辺とその間の角の比が全て等しい
(iii)2組の角がそれぞれ等しい
この相似を用いて中線連結定理などの三角形の性質を考える。
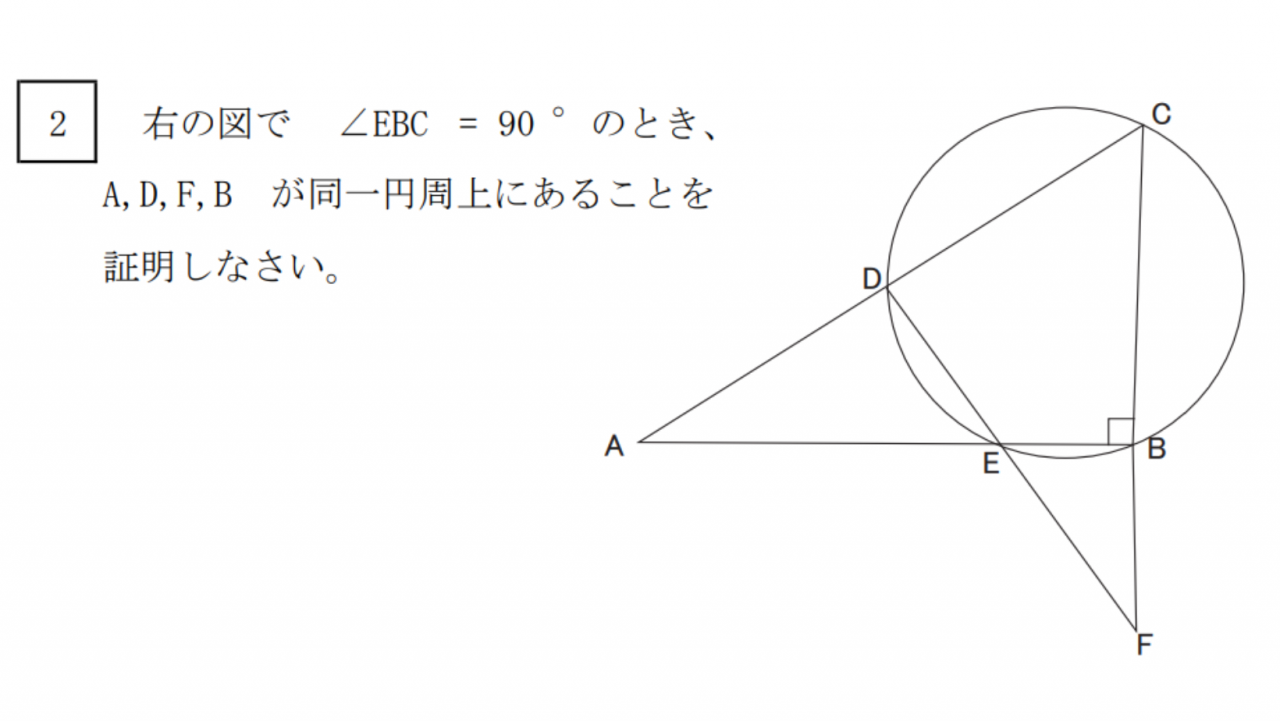
⑥円周角と中心角
この分野で最も重要な定理のうちの一つは円周角の定理だ。
この定理は円周角の角度が中心角の角度に一致するというものだ。この定理から円の中心を通る直線を含む三角形は全て直角三角形になることがわかる。
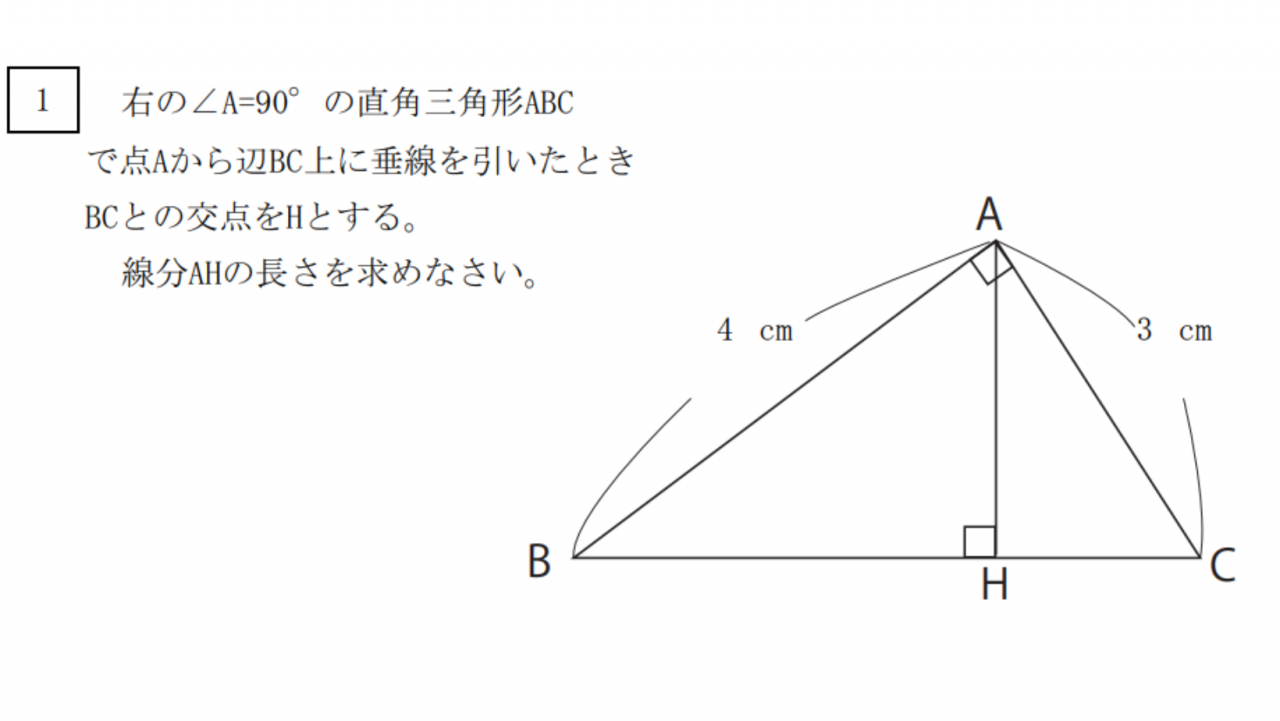
⑦三平方の定理
三平方の定理はピタゴラスの定理とも呼ばれる有名な定理です。
定理の内容としては「直角三角形の斜辺の長さの2乗は残りの辺の2乗の和と等しい。」というものです。
しっかりと有名な三角形を覚えることがこの定理を使いこなす上で重要になります。
⑧標本調査
標本調査は調べたい対象の一部を調査し全体を予測するものです。それに対して全数調査は調べたい対象の全部を調べるものです。
最後に
ここまで中学の数学の内容を重要な部分を摘んで話してみました。
忘れていたことはあったでしょうか?
数学の点数が伸び悩んでいる人はひょっとすると中学範囲や以前習った範囲に大きな抜けがあることが原因かもしれません。
今回読んでみた内容がすぐに出てこない場合は中学数学から復習して見ることをおすすめしますよ!
また勉強の仕方がわからない場合はぜひ一度武田塾の受験相談にいらしてください!
全力でみなさんの受験をサポートします!












