こんにちは。武田塾武蔵小山校講師のMです。
本日のブログはというと、数学オリンピックで出題された整数問題を解いて考えていこうと思います。
なんでいきなり数学オリンピックの問題を?と思う方も多いと思いますが、整数問題の「解法パターン」が分かっていれば、入試はおろか数学オリンピックの問題すら恐るるに足らずということをお伝えする為です。
ではさっそく問題へ…といく前に、整数問題の「解法のパターン」というものを軽く押さえておきましょう。
【整数問題】押さえておこう!「3つの解法パターン」
まず、整数問題で一番重要なことは何でしょうか?
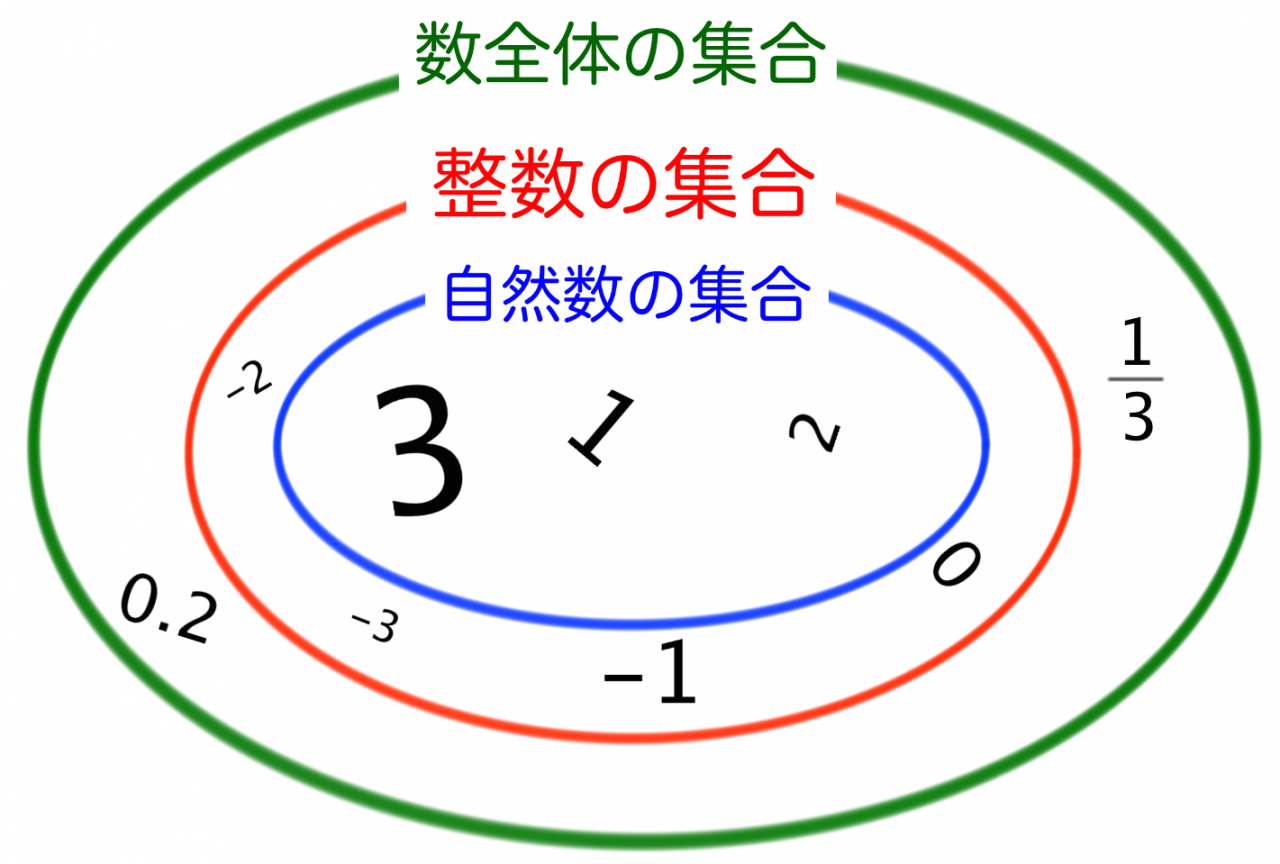
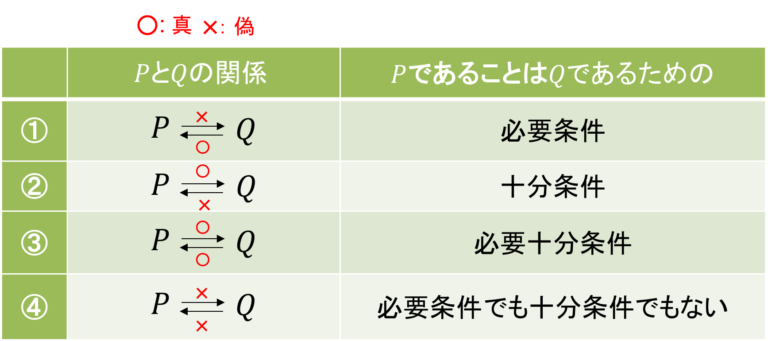
もちろん、1つ1つ見ると不定方程式やユークリッドの互除法などさまざまな解法を学ぶわけですが、もっと大きなくくりで考えると「必要条件から範囲を絞り込む」ということでしたね。
必要条件とは数学Ⅰの序盤で習うのですが、ここ整数問題で威力を発揮します。
必要条件はより厳格な定義が存在するのですが、ここでは「(解になるために)最低限満たすべき条件」とでも覚えておきましょう。
例えば、ある等式があったときに、左辺が2で割れるなら右辺も2で割れなければならないといった感じです。
ただ、これだけでは解を求めることはできません。
必要条件で絞った後にその条件をみたす整数ひとつひとつが本当に解になるかを代入して求める必要があります。
これによって十分性が確かめられて解として成立するということですね。
では、その絞り込む方法=「解法パターン」にはどんなものがあったか。これについては大きく分けて3つ解法が存在します。
整数問題「解法パターン①」
1つ目は因数分解(掛け算の形)です。
整数問題は整数しか解にならないので、(整数m)×(整数n)=(整数)の形が作れれば、約数の組み合わせによって整数m,nが求められますね。
素数やその累乗が式に登場したときも有効な手段ですね。素数は(素数)×1なので。
整数問題「解法パターン②」
2つ目は剰余(あまり)です。
これは整数をなんらかの数で割ったあまりで分類し必要条件を求めるというものですが、因数分解ができそうもないものに対してはかなり有効な手段です。
今回解く数学オリンピックの問題もこの解法に気付くことが突破口です。
整数問題「解法パターン③」
3つ目は、不等式(範囲)です。
自然数を求める問題では解は1以上なので”うまい”不等式を使うことで1≤n≤5のように上から必要条件で解の候補を押さえつけられると便利です。
使う不等式は何でもよいですが、その後ひとつひとつ整数を代入して調べられるくらいの個数に絞り込めるかが鍵です。
1/m+1/n=1/6を満たす自然数(m,n)(m≤n)のような問題でよく使われる常套手段ですね。
以上の3つが整数問題の「解法パターン」です。
ここまですんなり来れた方はたとえ東大・京大・東工大でも、数学オリンピックでも解法の突破口はつかめると思います。
ではいよいよ数学オリンピック2014日本本選の第2問で出題された問題を見ていきましょう。

【整数問題】いざ、問題へ!「数学オリンピック」
【問題】2^a+3^b+1=6^cを満たす自然数(a,b,c)の組をすべてもとめよ。
なんともシンプルな問題ですね。一見どこから攻めていけばいいか分からず手が止まってしまいそうですが、上で説明した3つの解法パターンを習得していれば、なんの怖いこともありません。
では上の3つの解法のどれを使えば解を絞り込めるでしょうか。
「解法パターン」を探れ!その①
まず、1つ目の因数分解はいかがでしょう。
右辺が整数の累乗なので左辺を(整数)×(整数)にできればいいのですが、現段階では因数分解はかなり難しいですね。
ただこれも何度か試行錯誤した結果なので、この問題を見てすぐに因数分解できないと決めつけてしまうのは禁物です。
のちに解答が進むにつれ因数分解できる形になるやもしれません。
「解法パターン」を探れ!その②
次に、3つ目の不等式ですが、これも厳しそうですね。
自然数を求める問題ですが、左辺も右辺も増加関数なのでうまく評価できないですね。
2^a+3^b≤6^cとかを試みても大して有効な条件は得られそうにありませんでした。
「解法パターン」を探れ!その③
よって、突破口となる解法は2つ目の剰余ということになりますね。
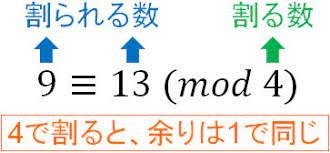
まずmod2で考えてみましょう。
2^a≡6^c≡0,3^b+1≡2≡0となるのでa,b,cがどんな数でもmod2すなわち両辺は2で割ることができます。
これだと絞れていませんね。
では次にmod3はどうでしょうか。
2^a≡(-1)^a,3^b≡6^c≡0なので、aが奇数の時に両辺は3で割れることが分かります。
これで第一歩です。
ただこれでa=2n-1などと置くのはあまりよくありません。もっといい絞り込みがあるかもしれません。
ほかの自然数で割ったあまりも考えていきましょう。
余談ですが、modは2,3,4,8,9を覚えておくと便利です。それぞれ一つの素因数の累乗なのでこういった問題には有効ですね。
mod2,3,4は皆さんも経験したことがあると思いますが、難問になるとmod8,9がたまに出現します。
mod2,3,4,8,9と続けて調べていくと、今回の問題はmod8を使うとうまくいくことが分かります。
まず、c=1のときについて考えます。
2^a+3^b=5となるのでこれを満たす(a,b)=(1,1)であることはすぐにわかりますね。
同様にc=2ののとき。
2^a+3^b=35となりaが奇数であることも考慮してa=1,2...と調べていくとこれもすぐに(a,b)=(3,3),(5,1)と求めることができます。
ではc≥3ではどうなるでしょうか。
この時、右辺は素因数2が3つ以上あるので8で割り切れることが分かりますね。
つまり(右辺)≡0(mod8)です。よって、左辺も8で割り切れることが「必要」となります。
そして、2^aを8で割ったあまりはa=1のとき2、a=2のとき4、a≥3のとき0となり、同様に3^bを8で割ったあまりはbが奇数の時3、偶数の時1になることが分かります。
なので(左辺)=2^a+3^b+1が8で割り切れるためには、a=2,b=(奇数)が必要となります。
むしろa=2,b=(奇数)の時にのみ(左辺)≡0(mod8)が成立します。
がしかし、これは先程のmod3で出たaは奇数という条件に反する為不適となり、c≥3のときは解が存在しないことが分かりました。
以上より(a,b,c)=(1,1,1),(3,3,2),(5,1,2)が求める解となります!!!
【整数問題】~まとめ~
いかがだったでしょうか。例え数学オリンピックの問題でも、「解法パターン」を意識して考えていけば突破口が開けることは伝わったでしょうか。
mod8で考えることができなかったという方はひらめき不足ではなく「経験不足」なだけです。
これらの解法パターンをしっかり身につけてさまざまな問題を解いていけばきっと入試の整数問題でまわりに差をつけることができるでしょう。
整数問題を恐れるな!ではまた。












