皆さんどうもこんにちは、武田塾武蔵小山校講師の須田です。
ゴールデンウィークが終わり忙しい日々が戻ってきましたね。
私も今年度から大学も対面授業になったので毎日死ぬ気で通学しています。
さて、実は私武田塾の外でも教務力向上のために講師をしています。
主に中学生や小学生を中心に指導しているのですが、常々思うことがあります。
それは、
「算数ってどうやって教えるのーーー!!???」
算数、おそらくこの記事を読む人にとっては昔通った道くらいの感覚しかないと思います。
中学で方程式というものを学べば算数は簡単なレベルですよね。
では、方程式というものを学んでいない小学生に、算数を教えることはできますか?
以前小学生の子に算数を教えた際、私はとても苦労しました。
今回はそんな問題に直面した私がどのようにして対処したのかを紹介しようと思います。

本当に小学生が方程式を使うべきではないのか
そもそも本当に小学生が方程式を使うべきではないのか。
文科省の定めた「学習指導要領」というものを調べたところ、特に小学生の段階で方程式を教えることを禁じる記述がなされていません。
また、朝日新聞デジタルの記事(https://www.asahi.com/articles/DA3S13928022.html)によると、神戸にあるあの難関私立中学の灘中学校や、東京にある私立巣鴨中学校も、受験生や保護者向けの説明会で方程式を使ってもよい、と説明したそうです。
では、なぜ学校や塾で方程式を教えてはいないのか。
それは小学生には正負の数の概念やその計算法、文字式の表記法とその計算法、項の概念や同類項をまとめる計算法など、方程式を使う上で必要な知識がまだ完全に身についていないからです。
これらを理解していれば方程式を使うことは何ら問題ないのですが、普通の小学生にそれは難しいです。
なので、算数では方程式を用いない計算法、具体的にはつるかめ算などの特殊算を使います。
教え方の例
前述の通り問題に直面した私は、まずネットを利用してどのように教えればよいのかを調べました。
そのうちのいくつかの例を紹介します。
つるかめ算
まず紹介するのは「つるかめ算」です。
これは名前を聞いたことがある人も多いと思います。
かく言う私も中学受験時代に重宝していた記憶があります。
つるかめ算の考え方を一般化して言うと、「2種類の量の合計から、それぞれの個数を求める」ってことになります。
要するに「連立方程式」です。
この「つるかめ算」はそのほとんどが算数で登場する問題になります。
「連立方程式」という考え方は中学生で習う事柄ですから、小学生はこれを連立方程式ではない方法(xやyなどの代数を使わない方法)を用いて解く必要があります。

実際に、問題を出してみましょう。
「50円切手と80円切手が合わせて35枚あり、合計の金額は1900円です。50円切手は何枚ありますか。」 (https://www.hello-school.net/sansub0702.htmlより引用)
連立方程式を既に知っている方にとっては対して難しい問題ではないと思います。
ではこれをつるかめ算を用いて解いてみます。
つるかめ算では図形を用いて問題を解きます。その図形は以下のようなものです。
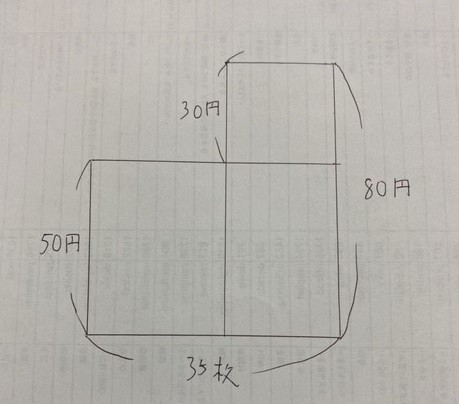
ここで図形の横線は枚数、短い縦線は50円切手、長い縦線は80円切手を表しており、図形の面積は合計金額になります。
ではまず下の横に長い長方形の面積を調べてみましょう。
50円×35枚=1750円ですね。
全体からこれを引くと上にある小さい四角形の面積は150円になります。
この四角形の縦線は80円―50円=30円なので横線は5枚になります。
ではもう一度図形を見てみてください。
この図形を縦線50円の四角形と縦線80円の四角形が合わさったものと考えて、横線を枚数だと考えるとどうでしょう。
この図形の面積が合計金額になるのが納得できると思います。
80円切手の枚数は5枚ですから、50円切手の枚数は30枚になります。
これがつるかめ算です。
連立方程式を知っている方にとっては非常に回りくどい解き方だと思います。
実際連立方程式を用いれば
50x+80y=1900
x+y=35
∴x=30、y=5
と3行で完結させられます。
この3行を体系的に表現したのがつるかめ算です。
旅人算
次に紹介するのは「旅人算」です。
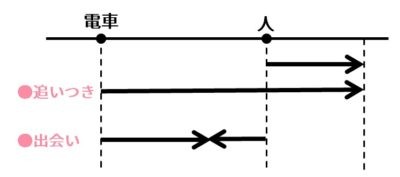
これは、2人が同じ道を歩いている状況で、2人の間の距離を求めたり、2人が向かい合って歩いているときの出会う時間やその速さ、あるいは、2人が同じ方向へ向かって歩いているときの追い越しにかかる時間やその速さ、といった数字を計算するものです。
たとえば、「Aさんが60 m/minで家を出発した25分後、Bさんが自転車で250 m/minの速さで追いかけたときの、追いつくまでの時間は?」といった設問が考えられます。
早速例題を出しましょう。
「A町とB町は4 kmはなれています。太郎くんはA町を自転車に乗って12 km/hで、花子さん はB町から歩いて4 km/hで同時に出発すると、2人が出会うのは何分後ですか。」 (https://www.hello-school.net/sansub1802.htmlより引用)
では解いて行きます。
太郎さんと花子さんはお互い向き合って12 km/hと4 km/hで進むので1時間で16 kmで距離が縮まるので、出会うのは4÷16=1/4時間後なので、15分後になります。
この旅人算は実際に私たちの暮らしの身近なところで活用されています。
電車のダイヤグラムも旅人算を使っています。
植木算
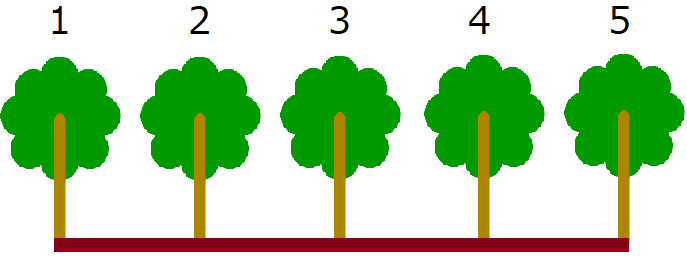
最後に紹介するのは「植木算」です。
物と物のあいだに存在する数に着目する計算になります。
では例題を出してみます。
「108mの道路に、端から端まで4 mおきに木を植えていくと、木は何本必要ですか。」 (https://www.hello-school.net/sansub0302.htmlより引用) 解いていきましょう。
まずは木の間隔は4 mですから、108 mまでの中に間の数は108÷4=27個存在します。
なので必要な木の本数は間の数+1で28本になります。
難しい問題ではありませんね。
物と物の間の数が物の数-1であることを知っていれば簡単に解けるはずです。
実践した結果
以上の計算方法を実際に小学生の子に教えてみました。
すべて小学校で指導する内容なので問題なく理解してくれることができました。
特につるかめ算に関しては他の2つの方法と違い図形を利用するので理解が早かったと思います。
終わりに
いかがでしょうか。
実際に多くの人にとって小学生に算数を教える場面は少ないと思います。
しかし、私は今回の一件から物事に対するアプローチの仕方が一つではないということを学びました。
これは数学に限らずすべてのことに言えることですが、方程式という手段だけに固執せずにたくさんのアプローチをできるように、皆さんも日々の勉強を頑張ってください。












