武蔵溝ノ口駅・溝の口駅より徒歩3分
大学受験予備校・個別指導塾の「武田塾 溝ノ口校」です。
今回は、溝ノ口校の講師によるブログです。
内容は「物理で微積は使うべきか？」です。
だいぶ難しい内容ですが物理選択の人はぜひ見てください！
それではどうぞ！
物理で微積は必要ない？使うべき？
こんにちは。武田塾溝ノ口校講師の窪田です。
今回は物理で微積を使うべきかどうかについて考えていきたいと思います。
微積の歴史的背景
微分積分とはなんでしょうか？
歴史について少しお話しします。
みなさんは高校の授業で積分よりも先に微分を習うと思いますが、歴史的には積分の方がはるかに前から発見されています。
積分を数式的に扱うことはできなかったものの、「無限に小さいものを足し合わせる」という概念は存在していました。
紀元前における古代ギリシャの発明家アルキメデスは、二次関数と直線で囲まれた面積を曲線の内側に多数の三角形を作って無限に足し合わせることで求めていました（取りつくし法）。
しかし、任意の曲線に対してその面積を求める方法は確立されませんでした。
それから1700年ほど経った17世紀後半には、「砲弾の弾道を計算したい」というニーズがありましたが、重力に従って次第に落ちていき、刻々と進行方向を変化させる弾道の軌道をとらえる方法がありませんでした。
つまり、変化を計算する新しい数学が求められたのです。
その後ロベルヴァルやフェルマーの活躍があったのち、かの有名なアイザック・ニュートンは微分積分の基本定理を発見し、今まで全く違う分野だと考えられていた微分と積分が逆演算であることを示しました。
ここで重要なのは、微分とは数学から生まれた数学なのではなく物理から生まれた数学だということです。
みなさんが高校で習う物理は古典力学と呼ばれるものですが、これはニュートン力学とも呼ばれています。
ニュートンが微分積分を発見したことにより発展した古典力学を微分積分なしで学んだとして、その本質を理解することは可能でしょうか？
微積の定義と意味について
少し数学的な話をします。
微分の定義はご存知の通りf’(x)=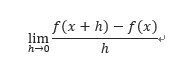
ですが、この意味は理解できていますか？
数2の微分しか習っていない人は「こんな複雑な式いちいち覚えられない！」「(x^a)’=ax^(a-1)だけ知ってればいいだろ！」と思うかもしれませんが、そんなこと言ってたらニュートンに怒られてしまいます。
(x^a)’=ax^(a-1)を含め基本関数の微分は当然暗記すべきですが、これらはすべてこの定義式から導かれたものであることを忘れてはいけません。
「f’(a)とは関数f(x)の点x＝aにおける接線の傾きである」ということをわかっていれば、こんな定義式簡単に思い出せます。
次の図を見てください。
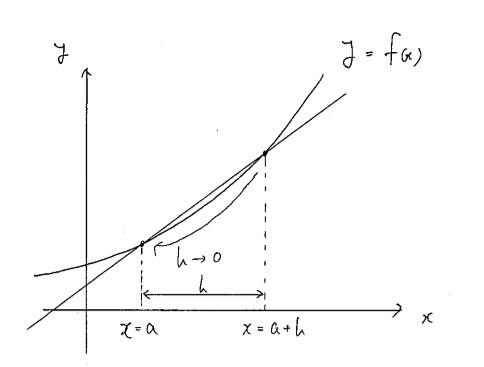
関数y=f(x)において2点x=aとx=a+hを取ります。
この2点を結ぶ直線は赤線で示したもので、この直線の傾きは（ｙの増加量）/（ｘの増加量）より{f(a+h)-f(a)}/hとなります。
では、このときｈを極限まで０に近づけたらどうなるでしょう？
想像してみてください。
だんだんx=aにおける接線に近づいていくと思いませんか？
これでf’(x)=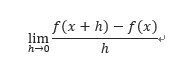はもう忘れることがないでしょう。
教科書にはf’(a)=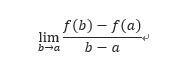
という風に書いてあるかもしれませんが、これはx=a,x+h=bとすれば同じ意味になります。
微分の定義がわかったところで次はdxとdyについて考えてみましょう。
f’(x)とは関数の接線の傾きであり、dy/dxとも書きます。これは傾きが（ｙの増加量）/（ｘの増加量）であることからdyがｙの微小増加量、dｘがｘの微小増加量であると考えれば納得がいくでしょう。
また、例えばy=ax+bという関数があったとき、y’=aと安易に答えてしまいがちだと思いますが、これはyをｘで微分したときの答えであり、もしｙをbで微分したらy’=１となります。
このように、関数を何で微分したかを明確に示すためにdy/dxという表記を使い、これはｙをｘで微分したことを示します。
よってy=ax+bにおいて、dy/dx=aであり、dy/db=1なのです。
では積分に出てくるdxについて考えてみましょう。
積分を習いたての頃はｙをｘで積分することしかないので、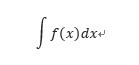
と書くべきところを
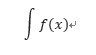と書いてしまう人がたまに見受けられますが大変けしからんです。
関数の面積を求める積分は無限に分割した長方形を足し合わせることであると教科書には図付きで書いてあると思いますが、このときf(x)は長方形の高さ、dxは(xの微小増加量なので)長方形の横幅を表しています。
この非常に細長い長方形を足しあわせる（∫はSのことでSumということ、すなわち足し合わせるという意味）ことで面積を求めるのですから、dxを省いてしまってはどうしようもありません。
また、関数を何で微分したのかが重要だったように、積分でも関数を何で積分したのかが重要になります。
f(x)をxで積分したのならちゃんとdxをつけてあげないと何で積分するのかがわからなくなってしまいます。
ではなぜ積分をするのでしょうか？
一定関数y=1について、ｘ軸とx=0とx=1に囲まれた面積はただの正方形なので１×１＝１とすぐに求まります。
これは積分で表すと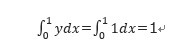
です。
この場合、ｙの値がｘによって変わらないことから積分を使わずとも1×1で求まりますが、本質的には積分をしているというのが重要です。
すなわち積分とは、ｘによって刻々と変化する値ｙに対してその積み重ねを計算できるということにその意義があります。
世の中には時間によってその値が変わる量（投げられたボールの位置、波の位相、交流電源の電圧など）がたくさんありますが、物理ではそれら時間によって刻々と変わる量を足し合わせるということをよくやります。
次項で具体的に見てみましょう。
具体的にどう使うべきなのか
前述したような背景がありながら、現行の高校教育課程では物理を微積を使わずに教えています。
したがって、高校物理の問題は微積を使わなくても解くことができるので、物理のどの場面で微積を使うのかわからない受験生は多いのではないでしょうか。
ここではひとつ、具体例を出してみようと思います。
最も代表的な微積を使う場面は位置、速度、加速度の関係について議論するときです。
位置ｘを時間の関数としてｘ(t)と書くとき、Δt秒後の位置はｘ(t＋Δt)となります。
このときの平均の速度は
となります。
しかし、一般に速度とは瞬間の速度のことを言います。
平均の速度を瞬間の速度に直すにはどうしたらいいか？
そう、Δtを限りなくゼロに近づければいいんですね。
つま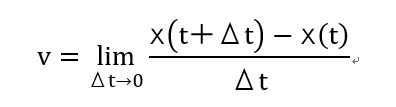り、
となり、
これはまさしく微分の定義そのものなので、
となることがわかります。
この式を変形して
としたあと、
両辺を積分すると、
となり、
これが位置の定義となります。
同様の議論を速度と加速度にも適応でき、
となります。
もう少し具体的に見てみましょう。
速度は距離÷時間で定義されます。新幹線で新大阪から東京までの550kmを2時間30分で移動すると、速度は550÷2.5＝220km/hとなります。
しかし、現実の新幹線は、途中で駅などに停まったりしますから、ずっと同じ速度で走っているわけではありません。
220km/hが表している のは、新大阪－東京間の速度の平均にすぎないのです。
新大阪を出発して60分後の新幹線の位置（新大阪からの距離）を205kmだとします。
そして、61分後の位置を209kmだとすると、この1分間での平均速度は、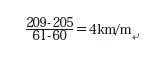
（240km/h）となります。
これを10秒間、1秒間、0.1秒間、と小さくしても計算は同じようにできます。
そして、時間の長さを限りなく0に近づけたとき、新大阪を出発して60分後の速度が求められるのです。
また、各時間の速度が分かっているとき、それを積分すれば移動した距離が分かります。
たとえば、60分後から10分間で移動した距離を求める場合、60分後は4km/m、61分後は3.8km/m…69分後は3.5km/mと分かっていれば、求める移動距離は、4+3.8+…+3.5というようにして求められます。
しかし、このままでは1分以内の速度変化に対応できません。
そこで、微分と同様に、1分ごとから、10秒ごと、1秒ごと、0.1秒ごとと小さくしていきます。
そして、切り分ける時間を限りなく 0に近づけたとき、正確な移動距離が求められるのです。
どんなに複雑に速度が変化していても、各時間での速度が分かっていれば、積分を使うことで移動距離が正確に計算できるのです。
このように、物理という学問自体微積のもとに成り立っており、物理を本質的に理解するために微積は必須である言えます。
高校物理は 微積は必要ない？
はい。解けます。
ただし、膨大な量の公式をわけもわからず暗記することができればの話です。
位置速度加速度の話に戻りましょう。
等加速度運動の公式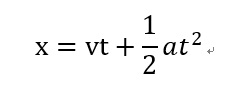
というのがありますが、
これは位置速度加速度の関係をわかっていればaをtで積分していくだけで求めることができ、
わざわざ暗記する必要がありません。
加速度をｔで積分すると速度になることから、aをｔで積分してv=at+v0
速度をｔで積分すると位置になることから、v=at+v0をtで積分してx=v0t+(1/2)at^2+x0
おわかりいただけたでしょうか？
微分 微分
位置 ⇄ 速度 ⇄ 加速度
積分 積分
の関係さえわかっていればこんな公式覚えるに値しないのです。
この他にも微積を使って導出できる公式はたくさんあり、大幅に暗記の量を減らすことができます。
また、これによって物理の根底にある原理が本当にごく少数であるということもわかってきます。
ただし、もちろん試験では暗記していたほうが素早く答えが出せるので暗記するに越したことはないです。
この他にも微積を使って導出できる公式はたくさんあり、大幅に暗記の量を減らすことができます。
また、これによって物理の根底にある原理が本当にごく少数であるということもわかってきます。
ただし、もちろん試験では暗記していたほうが素早く答えが出せるので暗記するに越したことはないです。
毎回導出するというよりかは試験中公式があいまいになってしまったとき、
ド忘れしてしまったときなどの検算として用いるといいでしょう。
具体例を１つ
高校物理の微積の実用的な出番をざっと書いていきたいと思います。
詳しくは自分で調べることをオススメしますが、ここはこういう計算をすれば楽に求まるんだなあ、そういう求め方もあるんだなあと思ってくれれば大丈夫です。
・仕事、エネルギー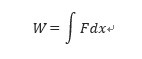
・力積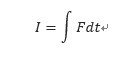
・保存力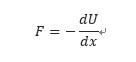
・電場による電位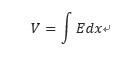
・コンデンサーの電流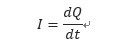
・コイルの電圧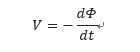
最後に・・・
かなり難しい原理的な話をしてきましたが、これらはすべて私が大学で習った知識をひけらかしているわけではなく、高校の時に東進の苑田尚之先生に教わったことなので高校生にも理解することは可能だと思います。
しかし、位置速度加速度の話は、物理で使う微積の比較的イメージしやすい部分ですが、先ほどの説明を見ての通り最低限の数学力が求められます。
なので、物理基礎のみを扱う文系にはオススメできません。
また、数学が苦手な子もやめたほうがいいと思います。
微積を使うのをオススメするのは早慶や難関国立を目指す人たちですね。
これらの大学の問題は微積を使ったほうがはるかに早く解ける場合が多いので、微積を導入することに対してコスパがいいと思います。
記述式の解答欄であっても、微積を使うことはまったく問題ありません。
微積を使ったからといって減点されることはあり得ないと思います。
まだまだ話し足りませんが、今回はここまでとします。
また機会があれば物理のことについて話したいと思います。
それでは受験生の皆さん、合格目指して勉強頑張ってください。
「もっと詳しく聞きたい」
「物理について議論をしたい」
という人はぜひぜひご連絡ください！
↓↓↓理系ブログ↓↓↓
【理系】芝浦工大・東京理科大など 私立理系特化型大学の特徴を紹介！
【理系】国立理系特化型大学の特徴を紹介！東工大、電通、農工大など
【国立理系】3科目以内で受験できる理系の国立大学を紹介します！
■無料受験相談 受付中■
志望校の話、文理選択、科目選択、勉強方法などなど
入塾の意思を問わず、どんな悩みや相談にも無料でお応えします！！
「何から始めればいいかわからない」
「勉強の仕方がわからない」
「全然成績が上がらない」
という方は、ぜひ受験相談にお越しください！
■武田塾 溝ノ口校Twitter■
【公式】武田塾 溝ノ口校です！
— 武田塾 溝ノ口校 (@tkd_mizonokuchi) September 11, 2020
受験生に役立つツイート・ブログを発信していきます！
ちなみに溝ノ口校では、受験生に役立つブログを350記事以上書いてきました！
ぜひ覗いてみてください！
⇓ブログ記事一覧https://t.co/dO9ujt99Gn
■武田塾 溝ノ口校に関するブログ■
■LINE■
溝ノ口校には公式LINEがあります！
LINEから受験相談の申し込みや勉強相談も可能です。
⬇︎登録できます⬇︎
■武田塾 溝ノ口校■
神奈川県川崎市高津区溝口1-18-6
溝ノ口第7三信ビル 5階
TEL:044-822-5222
