はじめに
こんにちは！武田塾京都校講師K.F.です。
今回もこれまでのブログと同じように数学の勉強法について解説していきます。
今日の単元は数学Ⅰの 三角比 です。
三角比は、高校数学の図形に関わる問題では毎回のように関わってくる単元です。中学のころに比べて高校の図形問題は、ひらめきの要素を必要としない問題が多く、図形問題のことがこれまで苦手だと思っていたような人たちも克服することが可能です。まずは基礎となるこの単元をがっちりと固めて高校の図形問題に立ちむかっていきましょう。
三角比を勉強する上でのポイント
単位円を活用しよう！
皆さん三角比の問題を解くときに忘れずに単位円を使ってますか？単位円は三角比の分野で最強の武器になります。
まず単位円の定義から復習しましょう。単位円とは「原点を中心とする半径1の円」のことです。
使い方は簡単です。x軸の正の向きとなす角が求めたい三角比の角度となるように原点から直線を引いてあげるとその円と直線の交点のx座標がcos,y座標がsin,直線の傾きがtanの値となります。
有名角のsin,cos,tanの値が問題において必要な時に、いつもどれがsin,cos,tanの値がごっちゃになってしまうなんて人いませんか？単位円を使いこなせれば有名角の三角比の値で迷ったりすることは無くなります！「鈍角なのにcosをマイナスにし忘れた・・・」なんてミスもなくなります。
三角比の相互関係
①sinθ2+cos2θ＝１
②tanθ＝sinθ/cosθ
上の２つの公式は必ず完璧に暗記しましょう。これから先、色々な場面で使うことになる非常に重要な公式です。
もう１つ、みんなすぐ忘れてしまう複雑な公式で1+tan^2θ=1/cos^2θという公式も相互関係の公式としてあるのですが、ここだけの話あまり使いません。とにかく最初にあげた２つの公式は使いこなせるようになりましょう。
②の公式に関してよく分母と分子のどちらにsinを置いて、どちらにcosを置くのか分からなくなってしまう人が多いです。そんな時は公式を覚えるにあたって１度公式の証明をしてみるのが、オススメです。
①の場合さっき紹介した単位円を利用すると簡単に証明できます。
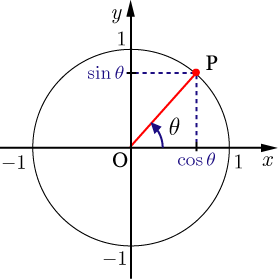
0＜θ＜90の時、上の単位円の（cosθ,0)の点をHとすると△OPHに三平方の定理を用いて①の式が導き出されます。
また、tanθはOPの傾きなので②が導き出されます。
θが鈍角の時でも同じような方法で導けるので、是非やってみて下さい。
このように一度証明をするだけで公式の定着率がぐんと上がり忘れにくくなるのに加え、たとえ忘れてしまったとしてもその場で導き出すこともできます！公式の証明は習慣づけていきましょう。
正弦定理と余弦定理
高校数学で三角形の図形問題があったら、９割くらいこの公式を使うことになります。重要なのでおさえておきましょう。
三角形の2辺の長さa,bとその挟む角の大きさθ（0度＜θ＜180度）が与えられている時、その対辺の長さcについて
ー①となる。これが余弦定理です。
余弦定理は基本「ある2辺の長さとその挟む角が分かっている時」に活用することができます！
また①の式をcosθについて解いて、cosθ＝・・・の形にすれば三角形の三辺の長さよりcosの値が出てθが何度かもわかります。
つまり「3辺の長さが分かっていて、角度を求めたいとき」も余弦定理は役立ちます。
次に正弦定理についてです。
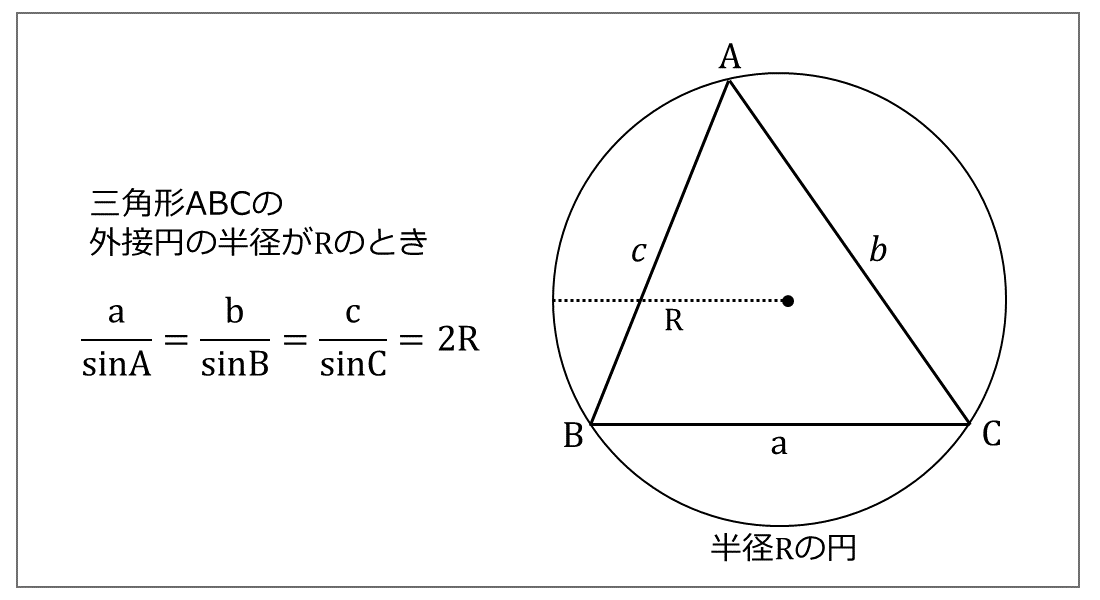
また、上の式の左の二つの等号部分だけ取り出した式はa:b:c=sinA:sinB:sinCと書き換えることもできます。
問題文で向かい合う角と辺のペアが与えられている時は、正弦定理を用いて外接円の半径を出したり、もう一つ何か角や辺が与えられていたらそれと向かい合う辺や角を求めることが手来ます。
これら余弦定理・正弦定理、三角比の相互関係を用いれば大抵の高校数学の平面図形には対抗することができます。どんな難問が出てきても、まずこの３つの公式が使えないのかを確認するくせをつけて行きましょう。きっとどこかにこれらの公式が使える条件が隠れているはずです！
円に内接する図形
皆さん中学校時代にならった円に内接する三角形、四角形の性質を覚えていますか？
高校で習う図形問題は中学で習った図形の性質は覚えていることが前提となって問題が作られています。不安な人は中学生のときに使った問題集や教科書を引っ張り出して、様残な図形の性質を復習しておきましょう。
ここでは、図形に内接する図形の性質を紹介します。三角比の分野では、円に内接する四角形の問題は頻出です。問題集等では応用問題として扱われることが多いですが、共通テストにも出題される可能性の高い有名な問題なので押さえておきましょう。
①左図のように、おなじ弧に対する円周角は等しい。今回の場合角ＡＱＢ＝角ＢＰＡ
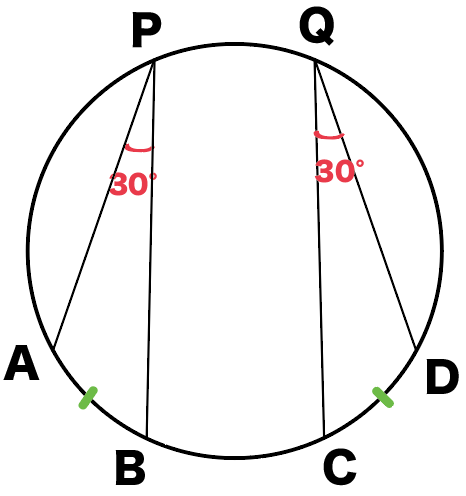②左図のように円周角が等しい弧・弦の長さは等しい。今回の場合角ＡＰＢ＝角ＤＱＣゆえにＡＢ＝ＤＣ，弧ＡＢ＝弧ＤＣ
③左図のように、円に内接する四角形において、向かい合う内角の和は180度。
どの性質を使うのかは問題によって異なりますが、③の性質は特に頻出なので、すぐに思いつけるようにしておきましょう。
まとめ
今回は数学Ⅰの三角比の勉強法について解説していきました。
図形問題は、受験にも頻出の単元でここで図形問題に対して得意という意識付けができると大学受験で大きなアドバンテージになります。本日このブログを読んで得た知識を上手く利用して、三角比の問題をマスターしちゃいましょう。
今回のブログは以上です。最後までお読みいただきありがとうございました。
武田塾は、「逆転合格」のノウハウをもった専門の塾・予備校です。
武田塾の勉強法を正しく身につければ成績は勿論、学力が上がり
そしてそれは皆さんの将来に必ず役に立つものです。
今の勉強法に悩んでたり諦めかけている人、目指している志望校と今はどんなにギャップがあったとしても武田塾で逆転合格を目指しませんか？
武田塾京都校には、そんな仲間が集まっています。
共に頑張りましょう！まずはお気軽に校舎に相談に来てください。
武田塾京都校 アクセス
京都の烏丸で予備校、塾、個別指導といえば！
大学受験の逆転合格専門塾【武田塾京都校】
〒604-8146
京都市中京区一蓮社町300 パームビル2F
(阪急烏丸駅、京都市営地下鉄四条駅・烏丸御池駅、徒歩４分！)
TEL：075-255-5777
武田塾では無料受験相談を実施中！
