はじめに
こんにちは!武田塾京都校講師K.F.です。これまでに引き続き数学の勉強法について紹介していきたいと思います。
今日の単元は数学Ⅰの 2次関数 です。
2次関数は、数学の苦手な人は「関数なんて無理…」とイメージだけで決めつけちゃいがちですが、高校数学の中では理解しやすい単元で、覚えるべきことも少ないのでコツさえつかんじゃえば得点源にすることも可能です!今回のブログを参考にして勉強を進めていきましょう。
2次関数を勉強していく上でのポイント
グラフを書こう!
みなさん中学生の頃を思い出してみて下さい。1次関数の問題を解くときに、毎回欠かさずしていたことがありますよね?
そう グラフを書く ことです!
これは高校の2次関数でも同じことです。今後出てくる3次関数、4次関数も含めた「関数」は、字数が大きくなり過ぎない限りは必ずグラフを書きましょう。式をじっとみているだけでは気づけないような思わぬ発見があるかもしれません
2次関数のグラフを書くためには、まず平方完成をする必要があります。その時平方完成をした後の式から必ず読み取ってほしい情報が3つあります。それは・・・
①グラフは上に凸であるか、下に凸であるか
②グラフの頂点の座標
③グラフのy切片
です
この3つの情報さえわかれば2次関数のグラフは書くことができます。なぜなら2次関数のグラフは軸を基準に左右対称なグラフだからです!
例えばy=x^2+4x+2という二次関数なら平方完成してy=(x+2)^2-2よって軸はx=-2です。軸からの絶対値(わかりやすくいいかえると軸からの距離)が2でおなじなx=0とx=-4を代入してあげるとどちらもy=2となります。また同様に絶対値3のx=1,-5を代入してあげるとどちらもy=7となります。このように軸からの絶対値が同じなxの値を代入してあげるとどの場合も同じになるので2次関数のグラフは左右対称だと分かります。
絶対値のついた関数
「y=|x|のように絶対値のついた関数のグラフを書け。」と言われたらみなさんは最初に何をしますか?数学の苦手な人達はいきなり座標平面上にグラフを書こうとして困惑してしまいがちです。
絶対値のついたままではグラフは書くことができないです…
絶対値付きの関数のグラフを書くときはまず絶対値を外してしまいましょう。絶対値の中身が正のときと負のときとで場合分けをします。
上の具体例で考えてみます。y=|x|はxが0以上のとき絶対値の中身は正になるのでそのまま絶対値を外してy=xとなります。またxが0より小さいときは絶対値の中身は負になるので絶対値のついた値は必ず正にならないといけないので絶対値を外すのと同時に-の記号を付けてあげてy=-xとなります。後はどの範囲でどのグラフの形をとるのかに十分注意しながらグラフを書いてあげましょう。
次に2次関数を例に考えてみましょう。y=|x^2-2x|のグラフを書くときにはまず絶対値の中身x^2-2xが正となる範囲と負となる範囲が知りたいので不等式x^2-2x>0を解いてみます。x^2-2x>0はx<0,2<xと答えが出るので上でやった問題と同じように解くとx<0,2<xの時y=x^2-2xでxが0以上2以下の時y=-x^2+2xになります。よってグラフは下記のようになります。
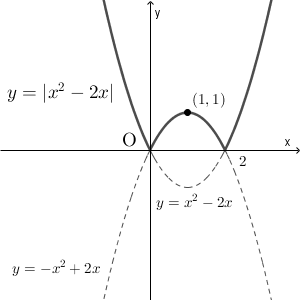
上のグラフを見て皆さん何か気付きませんでしたか?そうですy=|f(x)|のグラフはy=f(x)のグラフを書いてyが0以下の部分をひっくり返してあげればいいだけなんです。正直、上の2問の時のように丁寧にやる必要はグラフを書くだけだったらないんです。(でもy=x^2-|2x|みたいに式の全部が絶対値の中にあるわけではない式は別なので、上にやった2問のように丁寧に場合分けを行って解く必要があります。)
最大・最小
2次関数における最大値・最小値の問題を解くときに忘れがちなのですが、必ず注意して欲しいのは対象となっている範囲はどこからどこまでかということです。複雑な問題になればなるほど範囲の存在を忘れる傾向にあります。毎回範囲を意識して問題を解くことを習慣にしていきましょう。
また2次関数の問題で式を簡単にするために文字への置き換えや文字の消去をすることもあると思います。その際に置き換えた文字や消去した文字の制限から残った文字に範囲がつくこともあります。文字の取り扱いにむちゅうになってしまう人が多いため、これは特に忘れがちなので注意しましょう。
また2次関数の場合①対象となる範囲の両端もしくは②頂点のどちらかが最大値・最小値をよると決まっています。その3つの値の大小を比べるだけで問題が解けるんです!この考えは文字を含んだ複雑な問題になるとより重要性を増すので覚えておきましょう。
まとめ
今回は数学Ⅰの2次関数を勉強する上でのポイントを解説しました。
関数の問題は、ある程度機械的に解ける問題が多いので、数学な得意な人達は得点源としています。皆さんも今日ブログで得た知識を普段の学習に活かして関数の問題を得意にしていき数学が得意な人達の仲間入りをしちゃいましょう!
今回のブログは以上となります。最後までお読みいただきありがとうございました。












