偏差値の出し方とは?!
偏差値という言葉はよく聞くと思います。早い人は中学受験のとき、つまり小学生の時ですね。遅い人でも中学生のうちには初めて聞くと思います。
模試などを受けた後に「この偏差値じゃここは受からないよ!」などと言われたこともあるかもしれません。気づいた時には偏差値という言葉に振り回されていて、偏差値を上げなきゃと努力していると思います。
日ごろ使っている言葉の意味はしっかり把握しておいたほうがいいですね。数学の問題としても出題される可能性があるので一度は確認して覚えておきましょう!
まずは偏差値の計算公式は?
偏差値はつぎの公式で求められます。
偏差値 = 10×(自分の得点 – 平均点 )÷標準偏差 + 50
一応確認ですが、同じ計算式内に和差商積がある場合は商積を先に計算してから和差を計算します。
この場合は括弧がついているので、括弧内を一番優先して計算するべきですね。
上記の公式を見てみると、数字以外のよくわからない言葉が出てきたと思います。
その言葉をこれからひとつづつ確認していきたいと思います。
自分の得点
これは自分がテストで取った点をそのまま入れたらいいですね。
たとえば、英語のテストで80点を取ったら80点。
64点を取ったら64点とそのまま入れてくれればいいです!
平均点
これは受けたテストの平均の点数です。
平均点はテストの難易度や受けた人の能力によって変わってきます。
平均点の出し方の公式は一般的には
平均点=(データの合計値)÷(データの個数)
となります。
テストの平均点でいうと、
(全員のテストの合計点)÷(受験者数)
を計算することにより、平均点が出ます。
標準偏差
まず、偏差値を求める公式を見たときにこれは何だと思うのが、標準偏差だと思います。
偏差値を求めるときに大事になってくるのが「標準偏差」です。
標準偏差は一言で表すと、点数のばらつきを示す数値です。
もう少し簡単に言うと「自分があと何点上がると偏差値が大きくなるか」を示しています。
そのため、標準偏差の値が小さい(=点数の差が小さい)ほど偏差値は上がりやすく、標準偏差の値が大きい(=点数の差が大きい)ほど偏差値は上がりにくくなります。
標準偏差を求めることで全体的なデータの傾向がつかみやすくなります。
標準偏差は、受験者全体の点数と平均点を使って求めます。
計算式は以下の計算式で求めることができます。
① データ全体の平均値を求める
② 各データから平均値を差し引いた「偏差」を求める
③ ②で算出した偏差の2乗の和(分散)を求める
④ ③で出した偏差の合計を出す
⑤ 偏差の合計をデータの総数で割って分散を求める
⑥ ⑤で出した分散の正の平方根を求める
これによって偏差値が求まります!!
具体的な値で計算してみよう!
始めて計算する人も多いと思うのでまずは簡単な数値で計算していこうと思います。
数学を計算したときのデータを例として3人が以下のような得点を取った時に、3人の偏差値はどうなるのか計算していこうと思います。
Aさん 71点
Bさん 80点
Cさん 89点
①
まずは平均点を求めます。
(71+80+89)/3=80
よって、平均点は80点だと分かりました。
②次に偏差を求めます。
得点 偏差
Aさん 71点 -9点
Bさん 80点 ±0点
Cさん 89点 +9点
これで3人の偏差がわかりました。
③,④,⑤次は分散を考えます。
s^2={(-9)^2+0+(+9)^2}/3
=54
⑥分散の正の平方根を求めると、
s =3√6
≒7.35
これで標準偏差が求まりました。
ここからAさんの偏差値を求めていこうと思います。
もう一度定義を確認していくと、
(偏差値)
= 10×(得点 – 平均点 )÷標準偏差 + 50
なので、Aさんの偏差値をここから求めていくと
10×(71-80)÷7.35+50
=37.8
上記のようにAさんの偏差値が求まりました。
またBさんについて考えていくと、得点と平均点が同じため一瞬で偏差値が50と分かります。
これより、平均点を取った生徒は偏差値が50になることはどの場合においてもそうであることが分かりました。
偏差値でおおよその順位が分かる?!
偏差値が分かったなら、順位もわかるのではないか?という方もいると思います。正確に上記の問いに回答すると”わかりません”という答えになります。何点を取る人がどのくらいいるかによって変わってくるのです。
ただし、成績が正規分布であると仮定した場合のみ,理論的には偏差値から順位を計算することができます。
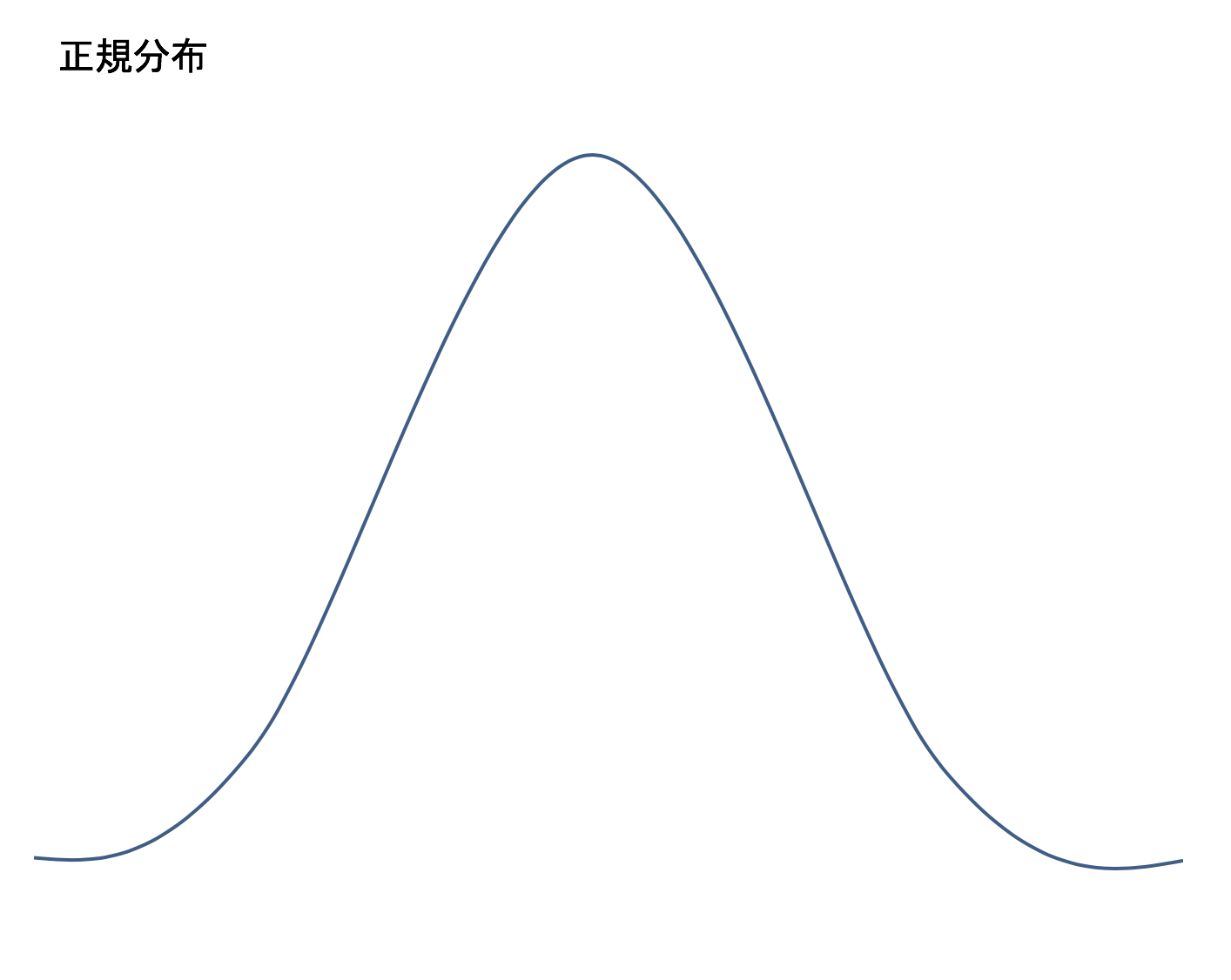
上記の図の凸部分の頂点が平均点のときのみです。
上記の場合以外の例を挙げると、
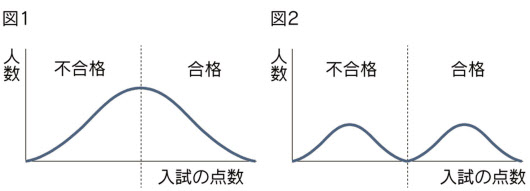
上記の図2のようになります。この例のように点線の平均点付近の人数が少なく、25%と75%付近の人数が多くなるような場合も考えられます。
下の表は偏差値により、上位何%の成績なのかがわかる表です。
たとえば、偏差値60ならば、上位16%の成績であることが分かりますから、全体数が800人だとすると
800×0.16=128位
ということになります。
表を見ると,偏差値55から偏差値58に上げるとすると全体数が100人の場合31位から21位まで10人追い越す必要があると分かります。
| 75 | 0.6% |
| 74 | 0.8% |
| 73 | 1.1% |
| 72 | 1.4% |
| 71 | 2% |
| 70 | 2% |
| 69 | 3% |
| 68 | 4% |
| 67 | 4% |
| 66 | 5% |
| 65 | 7% |
| 64 | 8% |
| 63 | 10% |
| 62 | 12% |
| 61 | 14% |
| 60 | 16% |
| 59 | 18% |
| 58 | 21% |
| 57 | 24% |
| 56 | 27% |
| 55 | 31% |
| 54 | 34% |
| 53 | 38% |
| 52 | 42% |
| 51 | 46% |
| 50 | 50% |
| 49 | 54% |
| 48 | 58% |
| 47 | 62% |
| 46 | 66% |
自分が持つ情報で偏差値を求めるには?
以上のように正確に標準偏差や偏差値を求めようとすると、自分のテストの得点以外の同じテストを受けた全員の得点情報も必要になります。しかし、必ずそのような情報が提供されるとは限らないことがほとんどだと思います。
そこで、標準偏差が分からない場合でも簡易的に計算する公式を使って、おおよその偏差値を求める方法があります。
この公式の場合に必要なのは、自分の得点と試験の平均点だけです。
50+(自分の得点-平均点)÷2=偏差値
自分の偏差値が気になる場合はこれを使う手もあると思います。
試しに計算してみるのもいいかと思います。
塾・予備校に通い始める時期は?













