【⇨はどっち？】「必要十分条件」って何？【武田塾国分寺校】

そんな疑問や不安を抱えている君！

武田塾では無料受験相談を実施しています。

近隣では国分寺校のほかに、

武田塾立川校（042-548-5977）

→武田塾立川校のHPはこちら！

武田塾武蔵境校（0120-769-977）

→武田塾武蔵境校のHPはこちら！

武田塾高円寺校（042-548-5977）

→武田塾高円寺校のHPはこちら！

でも無料受験相談を行っています！

ぜひ最寄りの武田塾の無料受験相談にいらしてください！

はじめに

こんにちは！武田塾国分寺校（042-312-0364）の大石です！

以前、数学の「絶対値」についての解説をしましたが、今回はそれの続編として、「必要十分条件」について解説して行きます！

なお、以前の絶対値の解説記事は以下よりご覧ください！

【躓いていませんか？】絶対値について細かく解説！【武田塾国分寺校】 - 予備校なら武田塾 国分寺校

新連載「数学を細かく解説！」スタート！第一弾は「絶対値」です！ 大学受験の予備校・学習塾・個別指導は逆転合格の武田塾の国分寺校まで。

https://www.takeda.tv/kokubunji/blog/post-276999/

いつ習ったっけ？

そもそもみなさん、必要十分条件をいつ習ったか覚えているでしょうか？

基本的に必要十分条件は高校１年生で履修する、「数学Ⅰ・A」の「集合と命題」で扱います。

他の分野と違い、計算を行わない独特な分野ですが、実はこの範囲、共通テストで頻出の分野になっています。

よく「どっちがどっちだっけ？」となることが多いこの分野ですが、コツさえ掴むことができれば満点を狙うのは容易いです！

逆に私大入試などでは出題されることは稀ですが、高得点勝負の共通テストに向けて、解き方のコツを教えます！

必要十分条件？

では早速、解き方のコツを教えていこうと思います！

まずは、下記の問題を見てみてください。

問．二つの自然数m,nに関する三つの条件p ,q ,r を次のように定める。

　p : m と n はともに奇数である

　q : 3mn　は奇数である。

　r : m + 5n は偶数である

このとき以下の問いに答えなさい。

　p は q であるための（セ）。

　p は r であるための（ソ）。

（２０１９年度大学入試センター試験数学Ⅰ・数学A第１問〔２〕より抜粋）

どうでしょうか？ほとんどの人がチンプンカンプンかもしれないですが、、、。

この問題を解説する前に、必要十分条件がどういうものなのかを解説しましょう！

必要十分条件とは？

必要十分条件とは噛み砕いて言うと、「ある事柄が成立するための条件」です。

例えば、ある人が国分寺に住んでいるとき、東京に住んでいなければなりませんよね。

つまり、国分寺に住んでいることが成立するための条件は「東京に住んでいる」ということになります。

これが必要十分条件の簡単な説明になります。

では今度は、必要条件と十分条件をそれぞれ見ていきましょう。

先の例に戻りましょう。

国分寺に住んでいるためには、東京に住んでいる必要があります。つまりここでは、東京に住んでいることは、国分寺に住んでいるための必要条件、ということになります。

十分条件とはシンプルにこの逆になります。

つまり、東京に住んでいるためには、国分寺に住んでいれば十分である。ここでは、国分寺に住んでいることは、東京に住んでいるための十分条件、ということになります。

これらのことを式として表すと以下のようになります。

「国分寺に住んでいる→東京に住んでいる」

ちなみにここでの矢印は、「ならば」を表します。

いかがでしょうか？これが必要条件と十分条件の説明になります。

ですがここでちょっとピンときた方もいるのではないでしょうか？

「「国分寺に住んでいる→東京に住んでいる」は成立するけど、「東京に住んでいる→国分寺に住んでいる」は成立しないよね？」と。

そうなんです！これが先ほどあげたセンターの過去問の答えにつながるのです！

ということで次は、必要条件・十分条件が「成立する」とはどういうことか、解説していきます！

必要条件・十分条件の成立

それでは、必要条件・十分条件の「成立」について説明します。

これらが成立するためには、「反例」が存在しないことが必要となります。

反例とは、「ある命題が成り立たない例」のことです。

先の例で言えば、東京に住んでいるとしても、三鷹に住んでいる人もいるし、世田谷に住んでいる人もいるがために成立しない、ということが言えますが、この「三鷹に住んでいる」や「世田谷に住んでいる」というのが「反例」になります。

なので、必要十分条件が成立するかを判断するためには、この反例があるのかどうを探してみましょう！

どうやって解く？

どっちが必要条件？どっちが十分条件？

ここまで聞いてみてどうでしょうか？必要十分条件がどういうものか理解できたでしょうか？

ではここからは、受験生が詰まりがちな、どっちが必要条件でどっちが十分条件なのかを解説します！

数学の参考書では、必要十分条件について、次のような説明がされています。

「命題 p ⇨ q が真（成立）であるとき、

　q は p （であるため）の必要条件、p は q  （であるための）十分条件。

p ⇨ q とq ⇨ p が共に真、すなわちp ⇔q が真であるとき、p は q（q は p） であるための必要十分条件である。」

（参照：数研出版　チャート式基礎からの数学Ⅰ＋A）

もちろん、それはその通りなのですが、これだけ言われてもさっぱりわかんない、という人もいるでしょう！ということで、必要条件・十分条件の判断の仕方を紹介します！

命題の真偽を使う方法

こちらは、先の必要十分条件の説明を踏まえたやり方になります。

このやり方は、

①. p ⇨ q が成立するかを判断する。

②. p ⇦ q が成立するかを判断する。

③. ①②が共に成立するなら、必要十分条件。①のみが成立するなら十分条件。②のみが成立するなら必要条件。どちらも成立しないなら必要条件でも十分条件でもない。

という手順になります。（ちなみに筆者はこのやり方を用いています。）

包含関係を使う方法

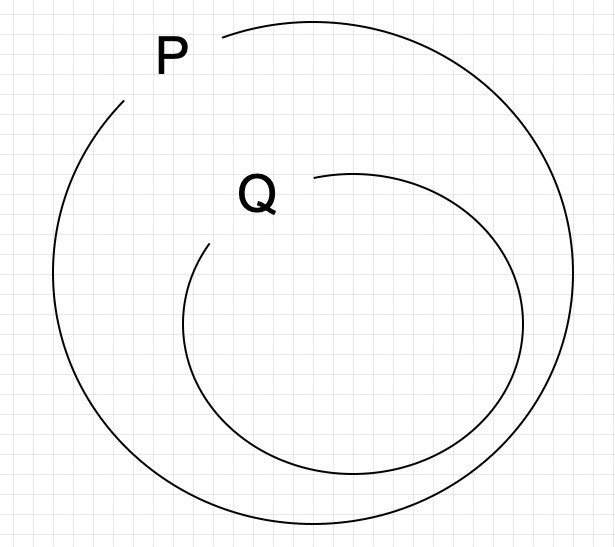
こちらは、必要十分条件を習う「集合と命題」の集合の分野を用いる方法です。

「条件p,qの表す集合をそれぞれ P, Qとするとき、上記のような包含関係にあれば、pはqであるための必要条件であり、qはpであるための十分条件であり、P=Qであるならば、pはq（qはp）であるための必要十分条件である。」

（参照：旺文社　数学Ⅰ・A基礎問題精講）

という考え方になります。

ただ説明されても難しいと思うので、実際の問題を使って説明します！（ここでは命題の真偽を使う方法を用います。）

問.x<1はx≦1の①必要条件である。②十分条件である。③必要十分条件である。④必要条件でも十分条件でもない。

解答

x<1⇨x≦1は真。x<1⇦x≦1は偽（反例：x=1）。

よって、解は十分条件ではあるが必要条件ではない。②。

いかがでしょうか？やり方さえわかってしまえば、あとは発想力次第！と言ったところでしょう！

ではそしたら、最初に書いたセンター試験の過去問を解いてみましょう！

問．二つの自然数m,nに関する三つの条件p ,q ,r を次のように定める。

　p : m と n はともに奇数である

　q : 3mn　は奇数である。

　r : m + 5n は偶数である

このとき以下の問いに答えなさい。

　p は q であるための（セ）。

　p は r であるための（ソ）。

（２０１９年度大学入試センター試験数学Ⅰ・数学A第１問〔２〕より抜粋）

一つ目、pとqについて。

p⇨qは真。p⇦qも真。よって、pはqであるための必要十分条件。

二つ目、pとrについて。

p⇨rは真。p⇦rは偽（反例：m=n=2）。よって、pはrであるための十分条件。

いかがだったでしょうか？

解き方さえわかれば、真なのか、偽なのかを判断するだけであることがわかったと思います。

このように必要十分条件は、方程式・不等式の解放や整数の知識がないと解き切ることが難しいです。

ですので、満遍なく数学の勉強をすることが大事！ということです！

まとめ

今回は、「必要十分条件とは何か」について紹介していきました！

必要十分条件は共通テストでは超頻出問題ですが、解き方さえわかれば、満点を取るのも容易です！

ですがそのためには、数学の苦手な分野をなくすことが非常に重要です！

ですが、「他の分野も手こずってる・・・」「定期テストに間に合わない・・・」

というような方もおられるのではないでしょうか？

そんな時は是非！武田塾国分寺校（042-312-0364) にご相談ください！

武田塾国分寺校では、「無料受験相談」というものを行っております。

受験や勉強に関するさまざまなお悩みを受け付けております。

ぜひ、お気軽にご相談ください！

皆さんのご来校をお待ちしております！