国分寺市/小金井市/小平市/国立市/立川市/調布市/府中市/多摩市/東村山市にお住まいの皆様、そして国分寺駅周辺で人気の学習塾・予備校をお探しの皆様こんにちは！
武田塾国分寺校（042-312-0364） です。
今回は、「三角形の五心」について解説していきます！
そんな疑問や不安を抱えている君！
武田塾では無料受験相談を実施しています。
近隣では国分寺校のほかに、
武田塾立川校（042-548-5977）
武田塾武蔵境校（0120-769-977）
武田塾高円寺校（042-548-5977）
でも無料受験相談を行っています！
ぜひ最寄りの武田塾の無料受験相談にいらしてください！
今回も以前から引き続き数学シリーズの記事になります！
第５回の今回は、「三角形の五心」がテーマとなります。
入試で問題として直接出題されることは他の分野と比べれば少ないですが、図形問題としては頻出の分野です。
共通テストでも出題率は高い分野ですが、種類が多く、紛らわしい分野でもあります。
今回はそんな三角形の五心について紹介していきます！
いつ、どこで習う？
解説を始める前に、今回もいつどこで習うのかどうかを確認していきましょう！
三角形の五心は、主に高校１年生で履修する数学Aの「図形の性質」という分野で扱います。
先に述べた通り、共通テストでは選択科目の一つとして出題されます。（図形が嫌いな人は選ばないでしょうが…）
私大入試では、あまり出題頻度が高いとは言い難いです。
三角形の五心、全部言える？
先ほどから「五心」という言葉を使っていますが、そもそもこの「五心」が何のことかわかっているでしょうか？
ということでまずは「五心」について整理しておきましょう！
三角形には、「五心」という言葉通り、５つの中心的な点があります。
名前を挙げると、重心・内心・外心・垂心・傍心の５つです！
これらについて、簡単にどのような点のことなのか説明します！
なお、今回の記事では図がたくさん登場しますが、全て筆者の手作りなので、多少のズレが出ていることがありますが、あらかじめご了承ください。
重心
重心は、文字通り三角形の重心のことを指します。
指で支えた時に、三角形が平行に安定する点、とも言い換えられるでしょう！
内心
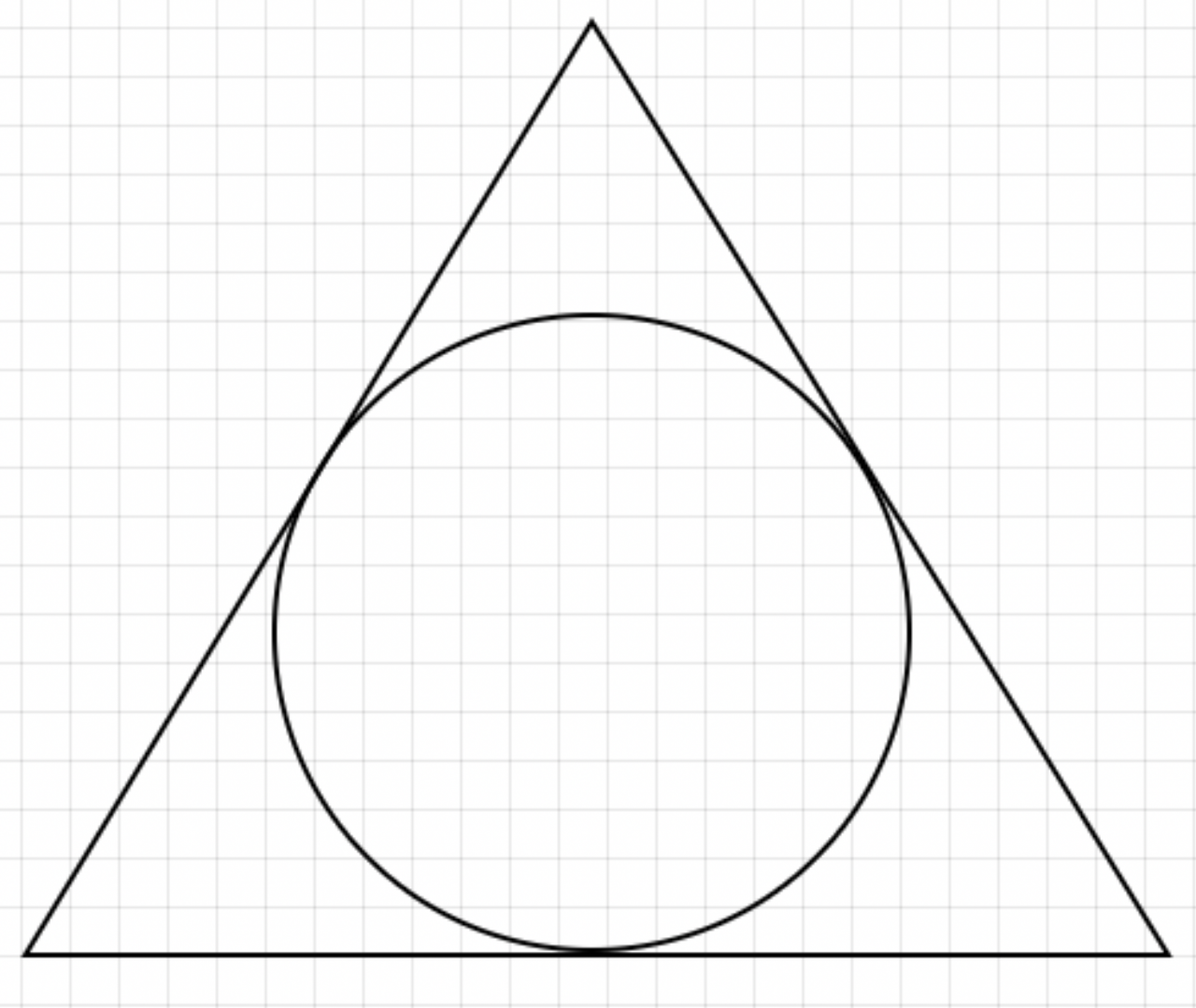
内心とは、上記の図のように、三角形に内側で接している円の中心のことを指します。
この円のことを「内接円」というふうに呼びます。
外心
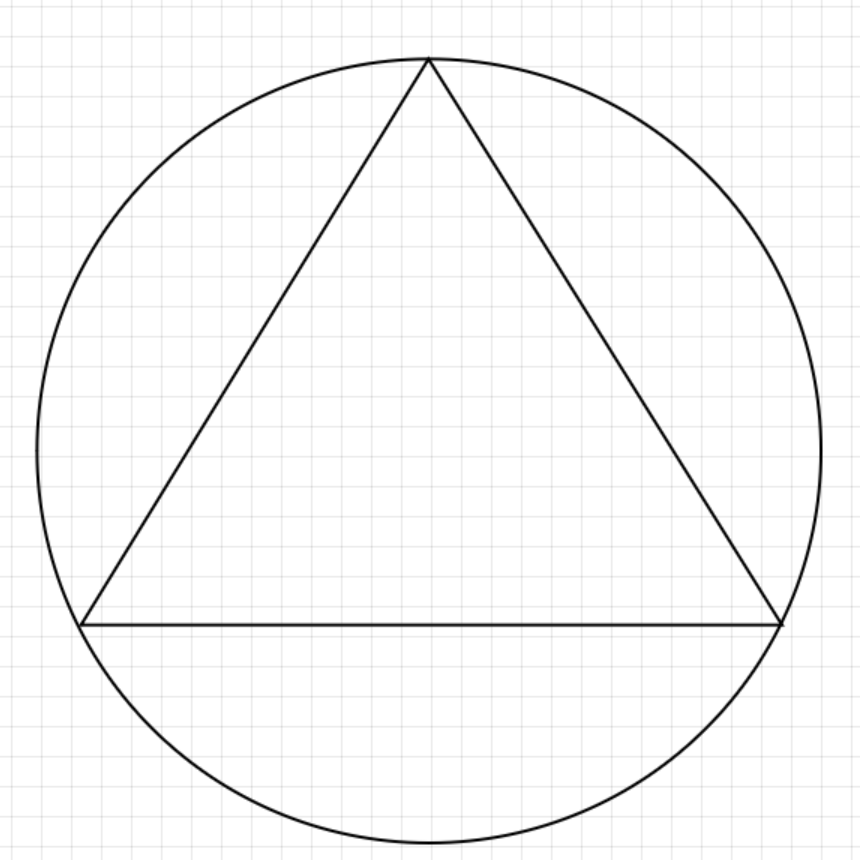
続いては外心です。外心は先ほどの内心とは対照的に、三角形に外側で接する円の中心のことを指します。
こちらの円のことを、「外接円」というふうに呼びます。
垂心
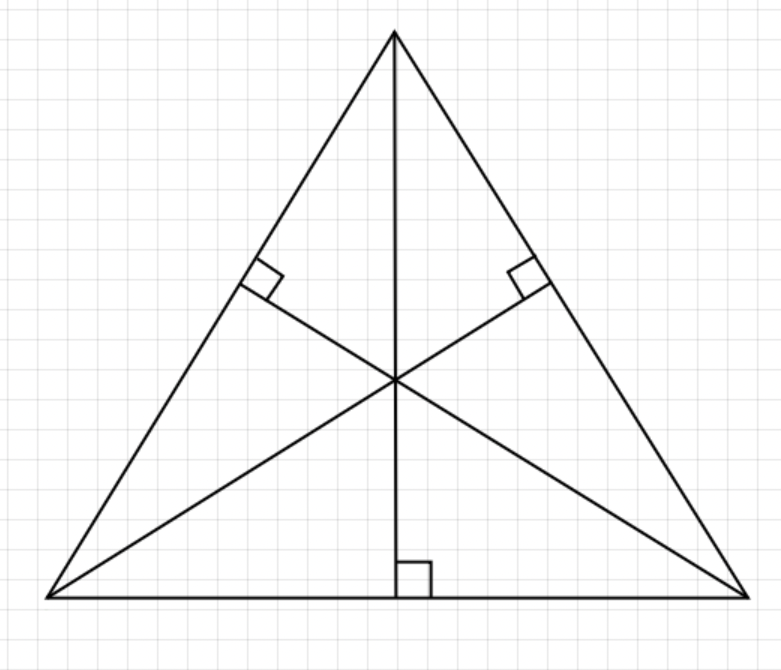
続いては「垂心」です。この「垂」という字は、「垂線」のことを指します。
垂線とは、ある辺に垂直に交わる線のことです。
つまり垂心とは上記の図のように、三角形の頂点から引ける３つの垂線の交点のことをいいます。
傍心
最後は「傍心」です。読み方は「ぼうしん」です。
「傍」と言われて何のこっちゃ！と思うと思うのでしょうが、安心してください、傍心が試験で問われることは滅多にありません！
ですが一応説明しておくと、「傍」とは「傍接円」のことを指します。
「じゃあ傍接円ってなんなんだ」ということですが、「ある三角形の一辺と他の二辺の延長線に接する円」のことを言います。
図で表すと下のような状態になります。
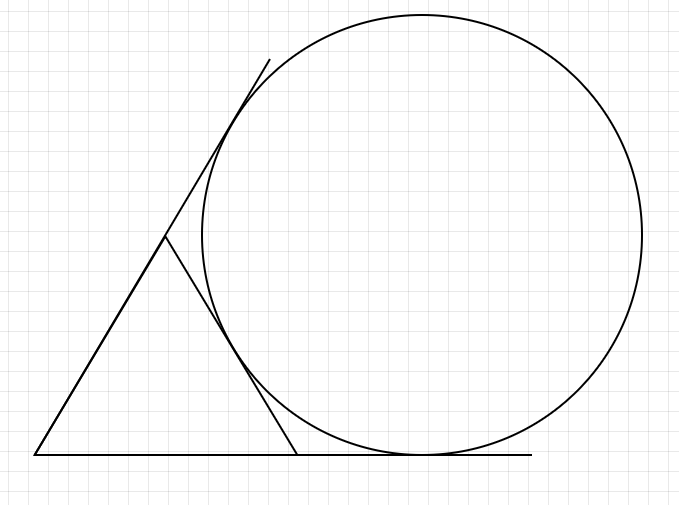
そして、この円の中心のことを「傍心」というように呼びます。
なおこの傍接円と傍心ですが、一辺と延長した二辺に接しているので、１つの三角形に対してそれぞれ３つずつ存在しています。
五心の求め方
さて、ひとまず五心を全て簡単に紹介しました。
ということで続いては、それぞれの求め方を紹介していきますが、その前に、これから出てくる用語をあらかじめ説明しておこうと思います。これらは、数学では非常に重要なものなので、知らなければ覚えておきましょう！
対辺：頂点の向かい側にある辺のこと（ある点が接していない辺とも言い換えられます。）
対角：辺の向かい側にある角のこと（ある辺が接していない角とも言い換えられます。）
垂線：頂点から対辺に垂直に降ろした線のこと
二等分線：角や辺を二等分する線のこと
中点：辺を２等分する点のこと（つまり、二等分線の一種とも言えます。）
中線：頂点から対辺の中点に引いた線のこと
内角：三角形の角のこと
外角：辺を延長してできる角のこと、角度は180度−内角となります。
重心の求め方
まずは重心から解説します！
重心の求め方は、「３つの中線の交点」です！
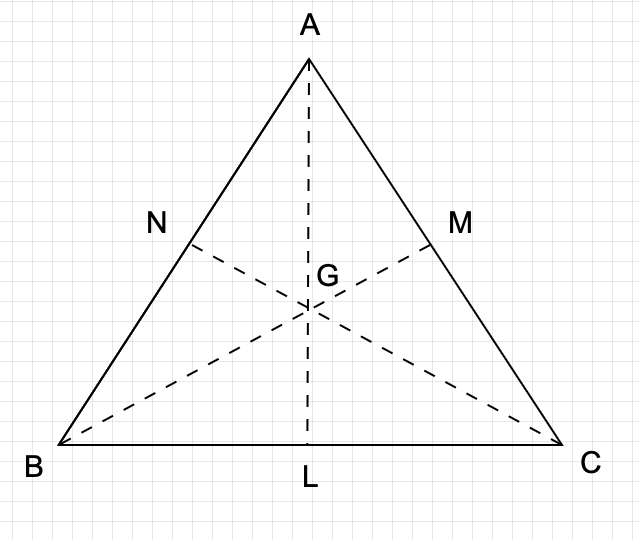
つまり、上記の図で言うと、AN:NB=BLLC=CM:MA=1:1ということになります。
また、重心には重要な特徴があり、AG:GL, BG:GM, CG:GNを2:1に分けるという特徴があります。
この特徴は図形問題でよく問われるところなので、絶対に覚えておきましょう！
内心の求め方
内心の求め方は、「３つの角の二等分線の交点」です！
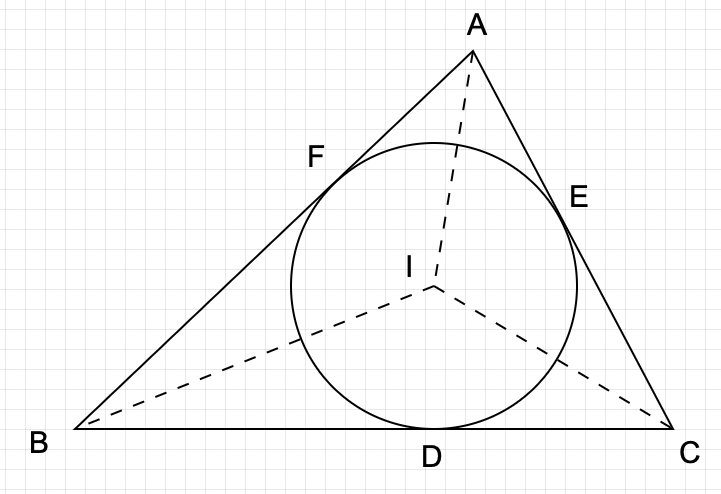
上記で言う、AI, BI, CIがそれぞれ角の二等分線ということになります！
また、円が接している３点、D, E, FからIまでの距離は等しくなっています。
その理由は、ID, IE, IFがそれぞれ円の半径だからと言うことになります。
外心の求め方
外心の求め方は、「各辺の垂直二等分線の交点」です！
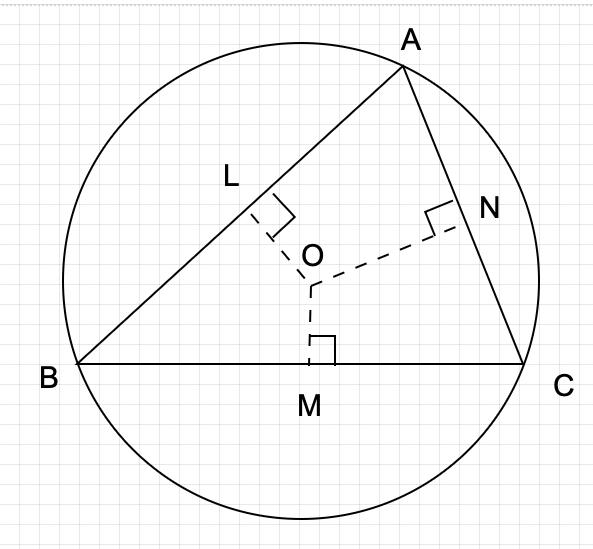
上記の図でいう、OL, OM, ONが、垂直二等分線というと言うことになります。
また、三角形が円に接している３点、A, B, CからOまでの距離は等しくなっています。
その理由は内心のとき同様、OA, OB, OCが外接円の半径だからです。
垂心の求め方
垂心の求め方は非常にシンプルで、「頂点から対辺に引いた３つの垂線の交点」です！
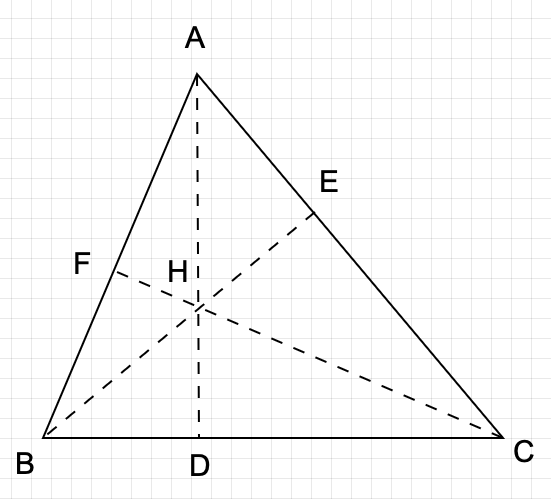
元々の定義が「３つの垂線の交点」である以上、垂線を引く以外どうしようもないです。
上記の図でいうと、AD, BE, CFがそれぞれ垂線、ということになります。
傍心の求め方
最後、傍心の求め方は、「一つの内角の二等分線と、それ以外の二つの外角の二等分線の交点」です！
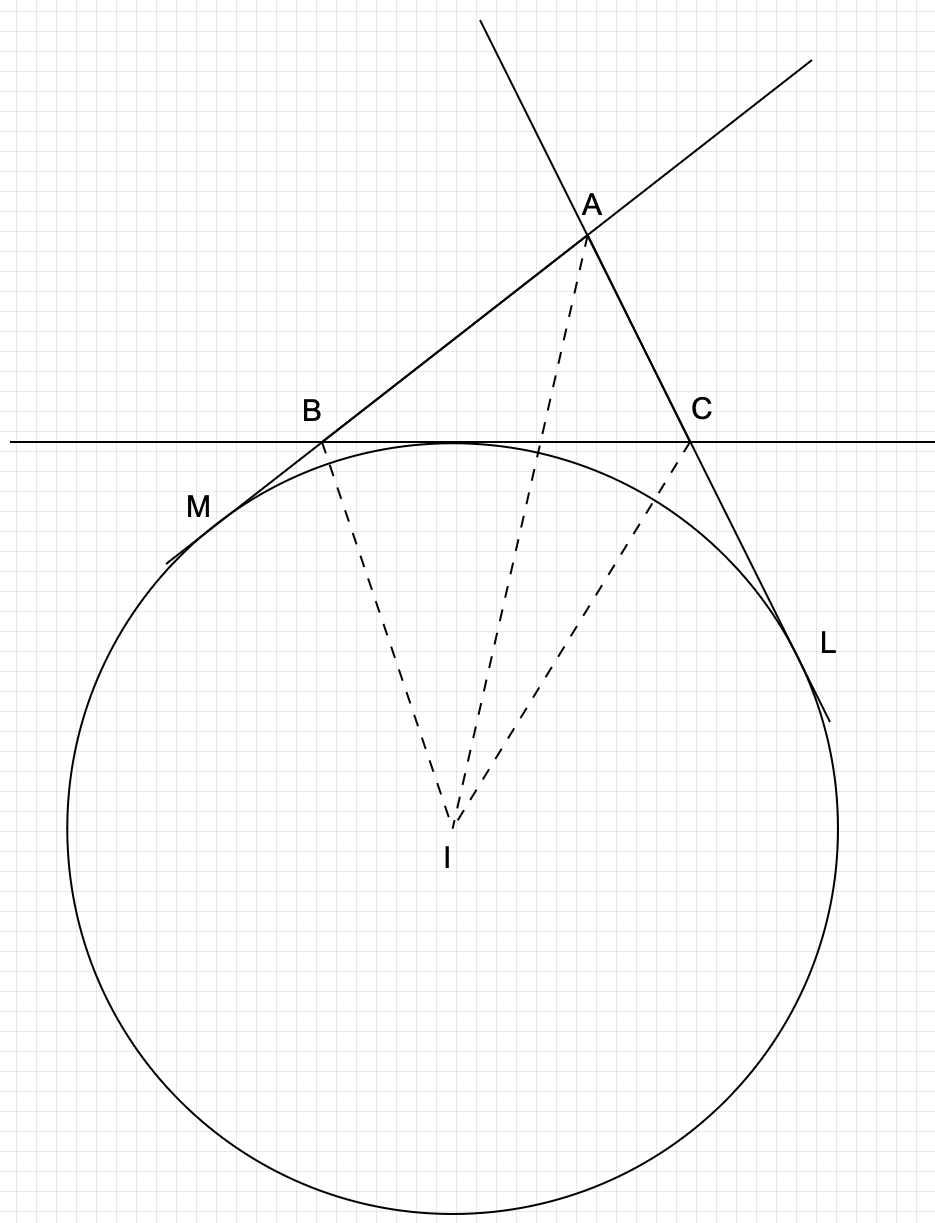
上記の図を見てください。今回は３つある傍心のうち、１つだけ図にしました。
上記でいう、AIが内角の二等分線、BIとCIが外角の二等分線になります。
外角の定義は先に述べましたが、この図を用いてあらためて説明します！
元の三角形は△ABCです。ですので、角は角BAC, 角ABC, 角ACBの３つになります。この３つの角を内角と言います。
そして、上記の図では辺AB, BC, CAがそれぞれ延長されています。その延長した辺と円の接点をM, Lとしています。
このとき、角BCLと角CBMのことを外角と呼びます。
そして、BI, CIがそれぞれ外角の二等分線、ということになります。
これらを他の２つにおいても行うことで、全ての傍心を求めることができます。
まとめ
今回は、「三角形の五心」について紹介していきました！
特に、重心・内心・外心は入試でもよく出てくるので、求め方や特性はしっかりと覚えておきましょう！
図形の問題は、そうした特性を使って解いていくことが多いので、覚えた上でそれを使えるようになることを大事にしていってください！
ですが、「他の分野も手こずってる・・・」「定期テストに間に合わない・・・」
というような方もおられるのではないでしょうか？
そんな時は是非！武田塾国分寺校（042-312-0364) にご相談ください！
武田塾国分寺校では、「無料受験相談」というものを行っております。
受験や勉強に関するさまざまなお悩みを受け付けております。
ぜひ、お気軽にご相談ください！
皆さんのご来校をお待ちしております！
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-
武田塾国分寺校
TEL：042-312-0364 FAX：042-312-0364
HP：https://www.takeda.tv/kokubunji/
住所
〒185-0021
東京都国分寺市南町3-17-2東海ビル2F
地図はこちらから！（Google Maps のサイトに移動します）
最寄り駅
JR中央線、西武国分寺線・多摩湖線 国分寺駅
南口より徒歩1分
受付時間
・月〜土
電話受付時間 10:00〜22:00
自習室利用可能時間 10:00〜22:00
毎週ブログを更新中！そのほかの記事はこちらから！
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-
武田塾の"冬季講習"開催中！！！
１１月１日(金)より、入会金不要で武田塾に通える「冬だけタケダ」「かけこみタケダ」の受付を開始しております！
冬だけタケダ：高校２年生以下対象
→詳しくは以下のブログをご覧ください！
【1/31まで申込可！】「冬だけタケダ」ってなんだ？【武田塾国分寺校】
かけこみタケダ：受験生（高校３年生、既卒生）対象
→詳しくは以下のブログをご覧ください！
【最後のチャンスを掴もう！】「かけこみタケダ」を紹介！【武田塾国分寺校】
受付期間は共に２０２５年１月３１日(金)までとなります。
詳しくは受験相談にお申し込みください。受験相談は、お申し込みフォームかお電話にて受付をしております。お気軽にお問い合わせください!
☆今年度の合格速報！！！☆
武田塾国分寺校から２０２５年入試の合格速報のお届けです！
実際に合格した生徒さんの合格体験記を公開中です！ぜひご覧ください！
【合格体験記 25’】部活で忙しい中でも勉強習慣をつけ東洋大合格！
【合格体験記 25’】基礎がわからない状態から総合型入試合格！
☆おすすめ記事☆
【副詞と接続詞の違いを解説！】あやふやではありませんか？英語文法
【１年経っても】野球の強い大学はどこ？？？【WBCロスです】
