【2024年版】数学のルートを徹底解説!武田塾参考書ルート
皆さんこんにちは!
神戸市兵庫区にある
武田塾神戸湊川校です!
GWも真っ只中、受験生の皆さんは思う存分普段より時間が取れますね!
さて、今回のブログでは
【2024年版】志望大学ごとの数学のルート
を取り上げます!
ということで、武田塾の参考書ルートを徹底解説しちゃいます!受験科目に数学がある方は必見です!
武田塾神戸湊川校では現在他塾に通われている生徒様で
勉強に悩まれている方の受験相談も受付しております!
お気軽にお問い合わせください。
是非、武田塾神戸湊川校の合格体験記もご覧ください!

武田塾の参考書ルートの構成
武田塾の数学の参考書ルートの構成は以下の通りになっています!
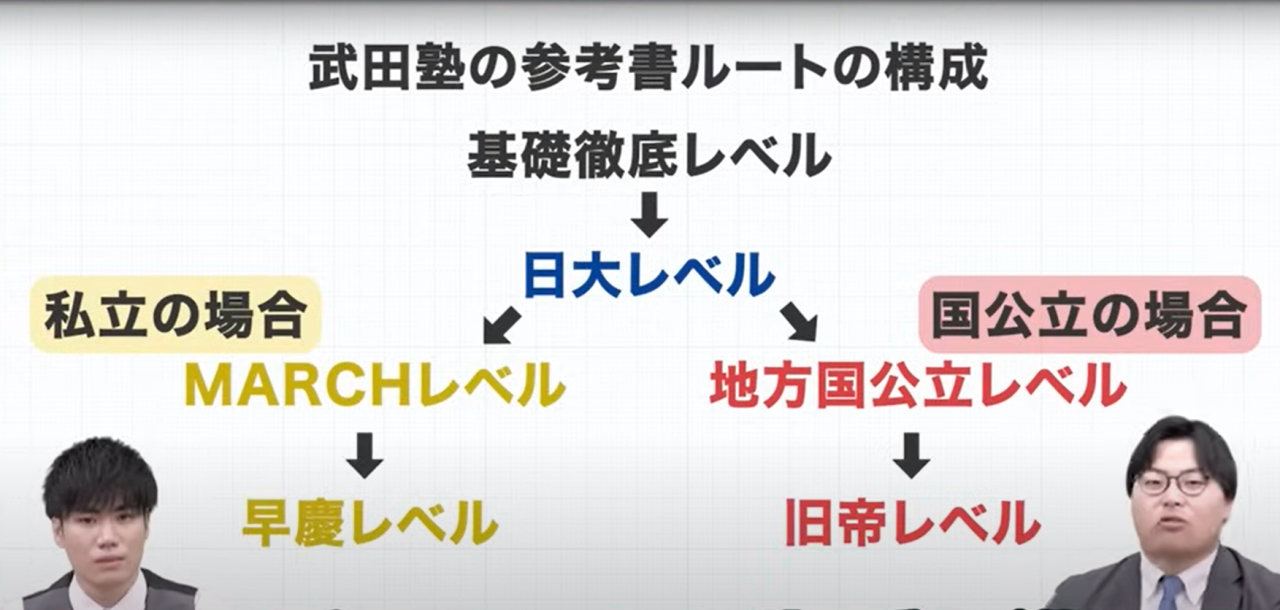
数学は、文系・理系に分けて各々解説していきます!
受験する学部により得点比重や対策の力の入れ具合が変わる科目が数学ですね。
ただし、【基礎徹底レベル→日大レベル】までは、文系・理系ともに使う参考書シリーズは同じです!
いくら理系が難しく範囲も広いとは言え、基礎を侮ること勿れということですね。
それでは早速レベル別に解説していきます!
基礎徹底レベル
対象者は以下のような状況に当てはまる人です!
「定期テストが赤点を彷徨っている」
「定期テストの平均点に届かない…」
「基本的な問題が心配」
「学校の授業についていくのがきつい」
具体的には、日大レベルである「入門問題精講」シリーズ・「基礎問題精講」シリーズを見ても、「よく分からない」という方におすすめです!

赤点の定義…が全国的に定まっているのか、はよく分からない点ではありますね。
ただ赤点・欠点にシビアな高専では、赤点60点・欠点30点だそうです。
赤点3回 or 欠点1回 で留年が確定するという噂もあるので、赤点はなんとしても避けたいところですね…!
ちなみに私の高校には、赤点・欠点という概念はありませんでした!
取り組むべき参考書
 基礎徹底レベルで取り組むべき参考書は上記の3冊です!
基礎徹底レベルで取り組むべき参考書は上記の3冊です!
「やさしい中学数学」を一通り解いた後に、「やさしい高校数学」「高校これでわかる問題集」を並行して進めていくルートです!
中学範囲の数学からさらっておくのが無難ですね。
というのも、学校の定期テストでつまずいてしまう人は、数学が昔から苦手だった人が多いからです。
自分の状況・必要性に合わせて、小学校数学から復習してみるのもありですね!
各参考書のおすすめポイント
特に「やさしい中学数学」のおすすめポイントは、中学3年間の数学を1冊で復習できることです!
数学が苦手な人でも約3週間で、中学3年間の復習を終わらせることができます!
数学や英語のように積み上げの教科では、土台が厳しい場合に、土台に立ち返ることが必要です。
次に「やさしい高校数学」「高校これでわかる問題集」を分野ごとに並行して解いていきます!
「やさしい高校数学」は解説がとても丁寧で分かりやすい参考書です!疑問が出ないように、余すことなく解説にページが咲かれています。全数学嫌いに知ってほしいレベルです!!
「学校の先生が何を言っていたか分からない・忘れた」「まだ習っていない」といったレベルでも、これを解けば、新しい単元の理解ができます!
武田塾の数学の方針には、「間違えた問題をその場でできるまでやる!」という真髄があります。
全問正解するまでやることがポイントなので、読んで終わりではなく、できるまでひたすら繰り返しましょう!
次に「やさしい高校数学」で解法をマスターしたら、「高校これでわかる問題集」にチャレンジしていきます!
この参考書の役割は、いろいろな問題のパターンを解き進めることにより経験値を積むことです!
そのため、基礎の何パターンを実際に演習できるような問題構成になっています。(下記の写真参照)

中身は完全にドリルのようになっているうえに、難しすぎる問題は割愛されています!
学校の4STEPやサクシードは思ったより、難しい問題も紛れ込んでいます。(余談ですが、私が使っていたときとデザインんが変わっています!オレンジのサクシードはもはや過去なんですね…)
逆に「やさしい高校数学」や「入門問題精講」「基礎問題精講」は良くも悪くも分野が凝縮されています。
即ち、短時間でコンパクトに抑えられはするものの、問題のパターンは決して多くはありません…。
しかし、数学苦手勢は、最早手が覚えるくらいまでいろんなパターンを網羅したいですよね。私もどちらかと言えば、理系科目はこのようなタイプでした。
これらを叶えてくれるのが「高校これでわかる問題集」です!
「やさしい高校数学」と「高校これでわかる問題集」を使い分けて、数学の基礎を分野ごとに習得しましょう!

定期テストでも全く同じ問題が出てくるわけではありません。
それも踏まえると、並行して解いていくことで、【「やさしい高校数学」だけ】よりも、遥かに実力がつくでしょう!!!
これらを定期テスト範囲ごとに完成させていくことで、抑えるべき点を押さえた証拠である平均点には手が届くことでしょう!
日大レベル
いきなり日大レベルから取り組んでもいい基準としては、以下に当てはまる方です!
「進研模試の偏差値が50以上」
「学校の定期テストで平均点以上取れている」
それでは取り組むべき参考書を見ていきましょう!
ここからは少しだけ文系・理系で分岐していきます!
【文系】取り組むべき参考書

分野ごとに「入門問題精講」「基礎問題精講」に取り組みつつも
それらと並行して計算力を強化する「ドラゴン桜式 数学力ドリル」に取り組んでいきましょう!
そして新課程の兼ね合いで「坂田アキラのベクトルが面白いほどわかる本」を「入門精講Ⅱ・B」の後にベクトルが苦手な人は取り組むことをおすすめします!(次の2冊)
(入門精講Ⅱ・Bにはベクトルがありません…!)
【理系】取り組むべき参考書

理系の人は文系との共通の参考書に+αで、「入門問題精講数学Ⅲ・C」「基礎問題精講数学Ⅲ・C」「ドラゴン桜式 数学力ドリル」にも取り組んでいきましょう!
ベクトルは、「坂田アキラの面白いほどベクトルがわかる本」ではなく、「入門問題精講数学Ⅲ・C」に取り組みましょう!
各参考書のおすすめポイント
ここからは各参考書のおすすめポイントを見ていきます!
最初は、「入門問題精講」です!(ピンクの表紙)
これは教科書の例題レベルを取り扱った問題集です。
写真は問題と解説の例です!

テーマの最初にテーマの概念から教えてくれます。
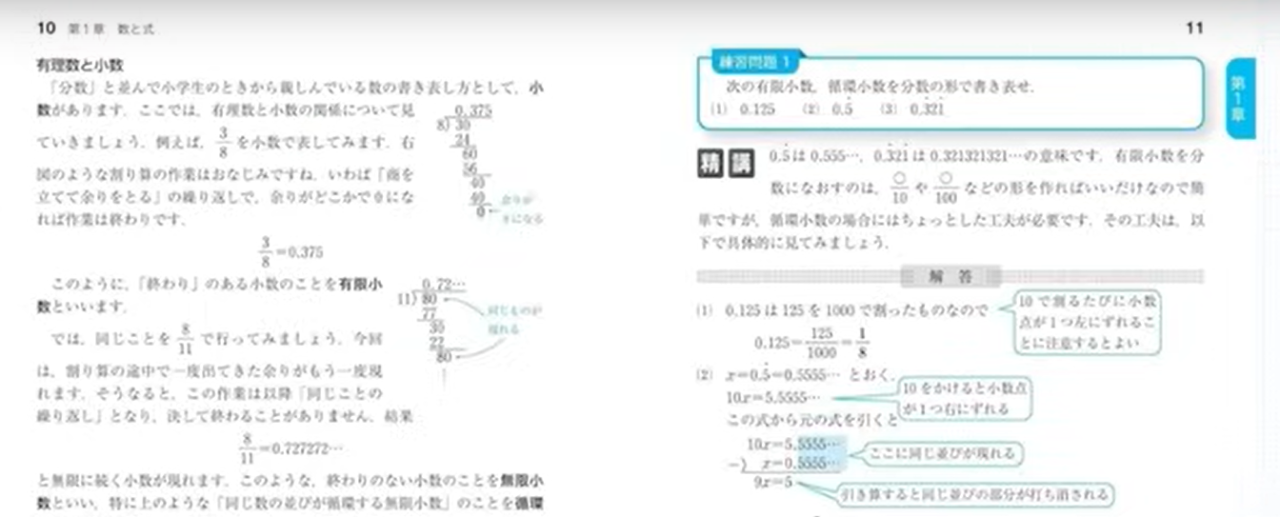
そして、問題・解説を繰り返して進みます!
解説は押さえるべき点がまとまっており、復習することで数学の本質が身につきます!解説の文字自体は多いものの、非常に分かりやすく説明がされています。
丸暗記やパターン化をしすぎて逆に何をしているのかが捉えづらくなってしまう人にもおすすめ!
数学を今後上のレベルまで力を伸ばしていこうと思ったときに、表面的な理解では先でつまずいてしまいます…。
しかし、基礎問題精講の解説を読むことから逃げなれば理解できる内容ばかりです!
分野・単元ごとの重要なポイントがかいつまんで説明されているため、分かった状態で問題を解くことが重要です!
たとえば、場合の数で考えてみると、順列と組み合わせの違いを明確に今説明できるでしょうか?
苦手な人はこんがらがちな単元だと思います。(ちなみに就活のときに割と多くの人が再び対面する羽目になります涙)
しかし、そもそもの場合の数・順列・組み合わせの考え方からさらっているこの参考書で学習さえすれば、そのような混乱も招くことはありません!
次に「基礎問題精講」です!(黄緑の表紙)
これは考え方の説明は省略されています。インプット用の参考書ですね!
というのも、学校の授業がある程度ついていけていて、定期テストでもある程度点数が取れている人向けの参考書であるためです。
だからこそ、「入門問題精講」の役割の重要性がより際立ちますね!
「考え方を理解して覚え進める」という意義を持って取り組むとより効果を発揮すると考えられます。考え方・解き方を覚えると、模試・過去問・入試問題等の初見の問題にも汎用でき、好成績を取ることに繋がります!
「入門問題精講」にて基礎of基礎を習得したら、「基礎問題精講」は本格的な問題演習の一環としての役割を果たしてくれます!
おすすめの解き方は写真の通りです!!

以下のように活用できると、なお良しです!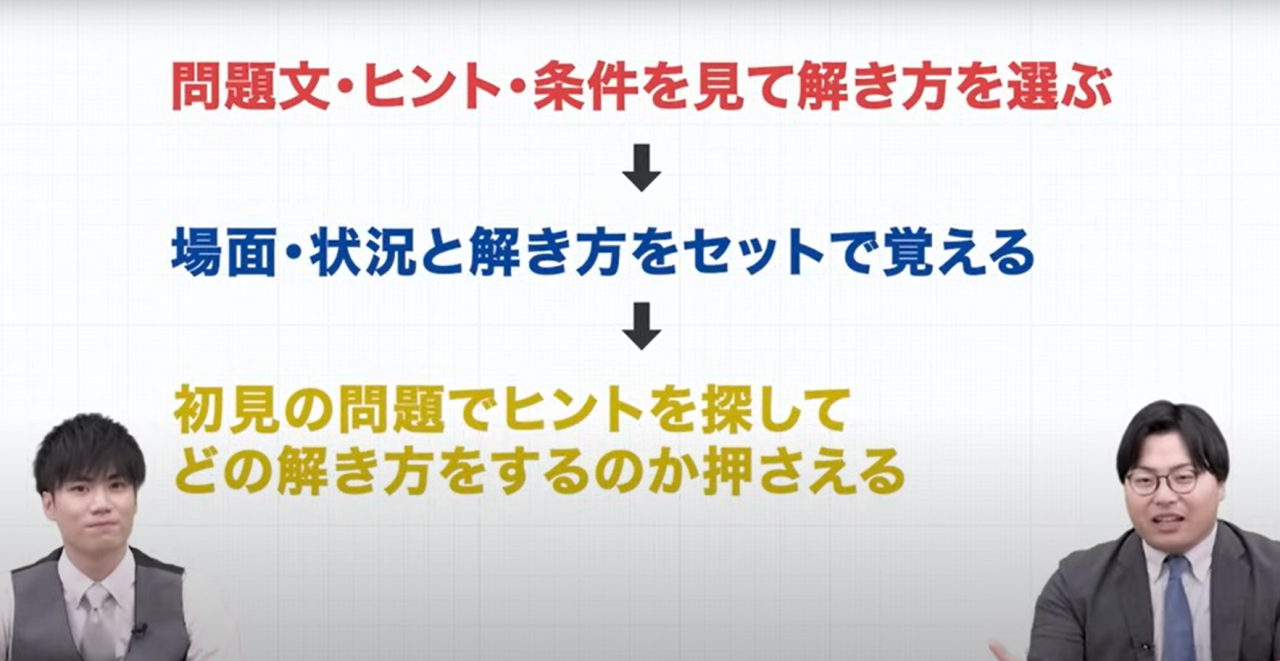
参考書1冊を最速で完璧にするための方法については、以下の動画で解説しています!
気になる方はぜひご覧ください!
学校でも数学の参考書は配られはすると思います。(チャート、レジェンド、フォーカスゴールド、サクシード、4STEPS…)
しかし、あれらを完全に使いこなせすには偏差値70以上ないと厳しいでしょう…。
分厚い辞書くらいの量があるため、挫折率が非常に高いです。なんと入門精講の3倍の量があります。あの量を繰り返し解くための時間を捻出することがまず難しいですね。
また解説も非常に簡潔であることが多いです。数学弱者にとっては、なぜその変形になるのかが一切できない解説も多々…。疑問点が多すぎて、スムーズに進められなかった苦い経験が多く蘇ります(白目)
仮に使用するとしても、入門精講を理解した後に、演習用としましょう!!
次に、並行して取り組んでほしい参考書が「ドラゴン桜式 数学力ドリル」
です!(緑と白の表紙)
計算練習用としての使用を推奨します!量やレベルが1番適切です!
「基礎問題精講」のデメリットである「計算量・演習量の不足」を解消するための参考書です!公式の計算をドリル形式で解くことができます!そのため、純粋にたくさん公式を使う練習をすることができます。
「基礎問題精講」でコンパクトに治す&短期間で仕上げた数学を、計算力で補いましょう。
計算が遅い人が多い単元はsinθ・cosθ・tanθやや数列のΣ、指数対数のlog等の計算に躓く人が多くなっています。
これらの単元は、沢山解くことで当たり前にすることが必要です。
難関大学を目指す人は、秒でできるようにするための計算力を「数学力ドリル」で身に付けましょう!
ただし、これは苦手な人に合わせて「数学力ドリル」を最小しているため、
もっと練習量を確保したい人は、学校で配られている傍用問題集(サクシード、4STEP)を使うのもいいでしょう。
さらに計算力に磨きをかけたい人は、「合格る計算」シリーズ・「試験時間と得点を稼ぐ最速計算」シリーズを使うのもいいでしょう。
そして、+αでおすすめする参考書が「坂田アキラのベクトルが面白いほどわかる本」です!(黄色の表紙)
基礎から根本が分かるので、ベクトルの理解を深められます。
ただし、「基礎問題精講」のベクトルで問題なさそうであれば、いきなり取り組んでも問題ありません!
最後に、おすすめしたいのが初登場の「大学入試数学 落とせない必須101選 スタンダードレベル」です!
この参考書は、数学Ⅰ・A/Ⅱ・Bの重要な問題を日東駒専レベルの問題を合わせて101題の問題が厳選されています!
「基礎問題精講」の後に実力チェックとして取り組むことが実はおすすめです!
「基礎問題精講」は問題自体は良問ですが、数学の勉強の仕方自体は非常に難しいです。そのため、単体ではちゃんと身に着けるのは難しく、それを補うために取り組むのがベストです!
数学は、アウトプットを、数字・文章が変わってもできるようにならなければ克服が難しい単元です。
そのため、他の問題に応用できる力がついているかを確かめることを目的として、「必須101題」に取り組んでください!
つまり、「基礎問題精講」での学習内容をアウトプットするための参考書ですね!
初見正答率が7割を超えていたら、「基礎問題精講」の内容が身についていたという判定になります!
逆に3~4割ほどの正答率であれば、「基礎問題精講」の使い方を間違えている可能性が高いです。丸暗記しているだけで、汎用ができず、意味がありません。
そうならないために、以下のような方法で解き進めていくことがおすすめです!


【番外編】理系向けに+α
Ⅰ・AとⅡ・Bがちゃんと正しい解き方で、初見の問題もアウトプットできる力がついていないと、数Ⅲ・Cはより難易度が上昇します…!
そこで、理系の皆さんは特にⅠ・AとⅡ・Bの状態で「大学入試数学 落とせない必須101選 スタンダードレベル」を解き、実力試しを行います。
そして、その実力試しをクリアした状態で、数Ⅲ・Cの勉強に入らないと、終了した段階で勉強のやり方を間違えているも、もう取り返しがつかない…という状況に陥り得ます…!たとえば、丸暗記で理解せずに解いていたとしても、1からやり直す時間を捻出することはおそらく難しいです。
【番外編】高1・高2で取り組むなら…!

ある程度学校の単元を抑えながら、横断して取り組んでいくイメージですね!
ただし、「入門問題精講」と「基礎問題精講」の章が食い違っていることもあるので、そこはうまく対応していきましょう!
実力試しに日東駒専の過去問を解き、ちゃんと力がついているかを確認しながら、次のレベルに進んでいきましょう!
【文系数学】MARCH・地方国公立レベル
MARCHも地方国公立も基本的に使う参考書は共通しているので、まとめて紹介します!
ここで使う参考書は以下の2冊です!
「文系の数学 重要事項完全習得編」(赤)
↓
「文系の数学 実践力向上編」(青)
各参考書のおすすめポイント
まずは「文系の数学 重要事項完全習得編」(赤)について!
このレベル帯で非常に解説が詳らかで、例題150題・演習も同量で、Ⅰ・AとⅡ・Bの重要な問題がまとめられています。
THE典型問題がまとめられており、入試問題でも受験生が確実に得点を稼がなければいけない問題ばかりです。
また解説が必勝ポイントという形で、「こういうタイプの問題はこういう考え方」というようにまとめられており、定石パターンを習得するのに非常に良書です。
「基礎問題精講」が仕上がっていれば、スムーズに取り組める参考書になっています!まさに積み重ねですね…!
「基礎問題精講」と同レベルでは、という疑惑も巷では聞きますが、「文系の数学 重要事項完全習得編」では、「基礎問題精講」の誘導が省かれています。普通の入試問題に準拠して作られているため、「基礎問題精講」よりかは、解くときの難しさがあると考えられます。
余裕があれば演習問題も取り組みたい!ところですが、時間がない受験生も多いと思います。そこで、時間がないけど取り組む場合は、例題をしっかりと固めて、例題150題をしっかりと身に着けていきましょう!!
MARCHで数学が易しめな青山学院大学の全学部日程や関関同立の関西大学・関西学院大学は、本当に時間がない場合、この参考書だけで挑む人もちらほらいるようです。
演習量が足りない場合は、演習問題まで解きましょう。
次は「文系の数学 実践力向上編」(青)について!
解説の細かさに関しては、赤と同じくらい素晴らしいです!
ただし、問題のレベルは(赤)に比べると上昇します。
しかし、ここを固めると、MARCH・関関同立・地方国公立で戦える範囲が広がります!
MARCH・関関同立は同志社の一部の難しい問題を除けば、十分合格点が取れるようになります!
国公立も大学のランクで言うと難しいですが、神戸大学・筑波大学・横浜国立大学・千葉大学辺りは、演習量が不足するものの、それ未満の大学であれば、「文系の数学 実践力向上編」に取り組むことで十分戦えます!
上記4大学については、演習量を補うために以下がおすすめです!
①「文系の数学」の例題だけでなく、演習問題まで解く
②「国公立標準問題集 CanPass Ⅰ・A・Ⅱ・B・C [ベクトル]」に取り組む
→この参考書は国公立でよく出る形式の問題をまとめてくれています!
そのうえで、計算が複雑な問題や、本物の入試問題かのような難しさも兼ね備えています。そのため、MARCH・国公立の上位の大学にも対応できます!
「文系の数学」シリーズの進め方は以下の通りです!

過去の武田塾の生徒で伸びる傾向にある生徒は、「文系の数学」シリーズの問題について「まとめている人」です!
その問題のどこがポイントなのか?解くための糸口はどこにあるのか?といった知識を蓄積していくことで、初見の問題のときの引き出しとして使うことができます!
特に「文系の数学」シリーズのように、数学の全範囲をわずか100~200問程度に収めている参考書は、一問一問に著者の意図が込められています。
膨大な問題パターンの中から、この考え方さえ知っておけば応用ができるもの・習得してほしいものを厳選してくれているわけです。
「個々の問題に何か習得ポイントがある」という気概で、問題に取り組んでみましょう!初見の問題での戦い方が圧倒的に変わるかもしれませんね。
【文系数学】早慶・旧帝レベル
使う参考書は2冊です!
「大学入試問題集 ゴールデンルート 数学Ⅰ・A・Ⅱ・B 応用編」
↓
「文系数学の良問プラチカ 数学Ⅰ・A・Ⅱ・B・C」
メインは「文系数学の良問プラチカ」です!
とはいえ、問題は難しく、解説も骨があるため、かなり大物ではあります…。
そのため、「文系数学の良問プラチカ」に行く前に、まず「大学入試問題集 ゴールデンルート」を挟みましょう!
各参考書のおすすめポイント
まず「大学入試問題集 ゴールデンルート 数学Ⅰ・A・Ⅱ・B 応用編」について!
これは問題を解くうえでの全体の設計図を意識する癖がつく参考書です!
なんと、わずか40問しかありません!大分コンパクトな量になっています。
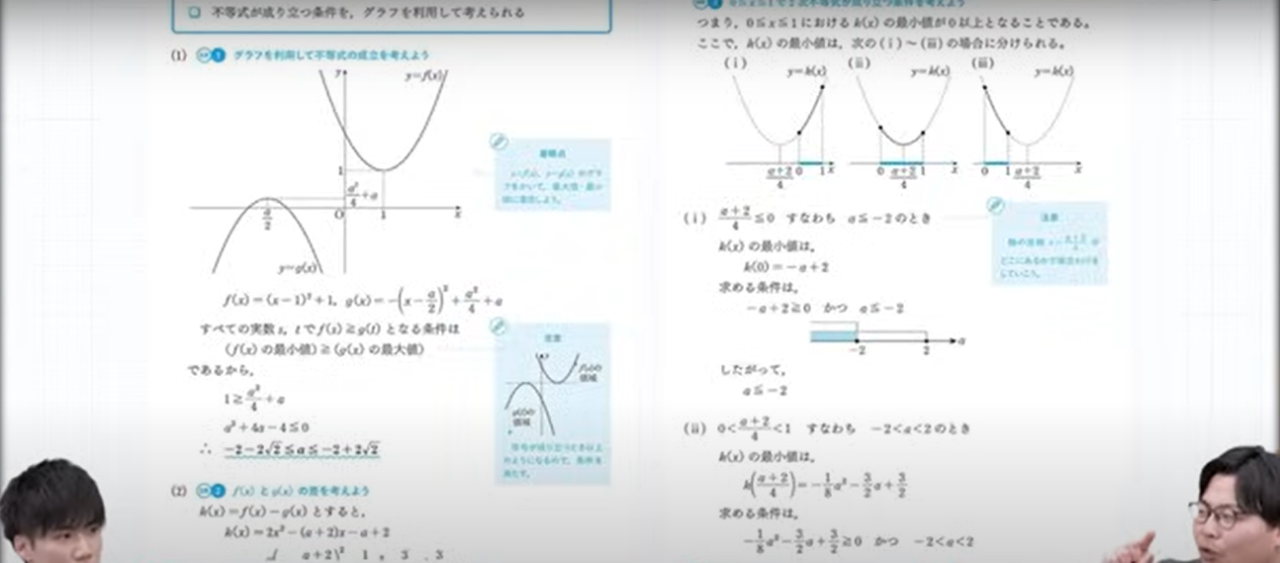
そして40題ですが、「正解へのゴールデンルート」という問題のプロセス・アプローチ方法がまとめられています!これを見て、解き方をマスターしていきましょう!
早慶・旧帝レベルになると、2~3段階くらい操作が必要であったり、分野が融合されていたりする問題も多いです。
すると、ダイレクトにその数値が求まることはありません…。
そのために、「ゴールデンルート」という考え方の部分が必要で、その参考書を通して、全体の設計図を描けるようになることが大事です!
40題を通して詳しい解説をもとに、早慶・旧帝レベルにも打ち勝つ術を身に着けていきましょう!
次に「文系数学の良問プラチカ 数学Ⅰ・A・Ⅱ・B・C」について!
早慶・旧帝の中でトップレベルで難しい大学である東京大学・京都大学・早稲田大学・慶應義塾大学・一橋大学志望の方は全部押さえておきたいところです。しかし、時間がない人は最初からやるのではなく、優先順位をつけて、出る分野から固めるという決断をすることも必要です!
そして、大阪大学・名古屋大大学・東北大学等であれば、自分が得意にしたいところを選んで取り組む方が伸びます!
ここら辺は残り時間との兼ね合いとの相談ですね。
ただ時間がない場合に、「ゴールデンルート」だけで合格するか否かという点に関しては、そのときの運次第というのが実情。
そのときの自分の状況や志望校、残り時間に合わせて、先生と相談しながらどのように進めていくか決めましょう。
しかし!どの大学であれ過去問演習は非常に大切です!
そして国公立であれば、共通テスト対策も非常に肝になってきます。別の田施策が必要になるので、また今後特集していきます!
【理系数学】MARCH・地方国公立レベル
使う参考書は以下の通りです!
「数学の良問問題集 [Ⅰ+A+Ⅱ+B+C]」
+αで「国公立標準問題集CanPass」
「実戦 数学重要問題集 数学Ⅰ・A・Ⅱ・B・C 理系」
を使っていきます!
各参考書のおすすめポイント
最初に「数学の良問問題集 [Ⅰ+A+Ⅱ+B+C]」について!
数学Ⅰ・AとⅡ・BとⅢ・Cの重要な問題がまとめて300問載っています!
いくつかレベルがあり、必須問題・確認問題・レベルアップ問題に分かれています!
まず全単元で必須問題→確認問題を回してから、最後に応用であるレベルアップ問題に取り組むのがおすすめです!

実は「数学の良問問題集」は1冊で、左側の3冊の参考書の役割を兼ねているのです!
理系数学は、数学Ⅲ・Cまでの膨大な量の入試問題の実戦を積まないといけないため、「数学の良問問題集」は時間をかけてじっくり取り組んでいきましょう!1冊仕上げるのにだいたい約3ヶ月ほどかかる本です。
「基礎問題精講Ⅲ・C」を一通り仕上げた人は「良問問題集」をじっくり固めていきましょう!
ある程度の国公立(神戸・筑波・横浜国立・千葉以外)はレベルアップ問題まで取り組むと、合格も狙っていけます。MARCHは問題ないです!
神戸・筑波・横浜国立・千葉大学志望の人も、レベルアップ問題まで取り組みつつ、追加で過去問演習を十分な機関取れるのであれば、合格点に乗せられる可能性が高くなります!
それくらい、「良問問題集」は1冊で比較的幅広く対策ができる優秀な一冊です!
解答・解説も非常に詳しく、問題も典型的で押さえておきたいものばかりです!躓きやすい部分のステップアップもスムーズにできるような問題が選ばれています。
次に「国公立標準問題集CanPass」について!
これは神戸・筑波・横浜国立・千葉大学や九州大学・北海道大学、そして明治大学・東京理科大学・同志社大学の理系を目指す人は追加で解いておきたいところです!
最後に「実戦 数学重要問題集 数学Ⅰ・A・Ⅱ・B・C 理系」について!
さらに演習を重ねたい人におすすめです。B以上のレベルの対策をすると、その分野はかなり強化することができます!
【理系数学】旧帝・早慶レベル
ここまで来ると、志望校別で使う参考書が変わります!
レベル帯によっては戦略別に使う参考書が変わります!
そこで、レベル別に分けて、解説していきます。
▼東大・京大・東工大・早慶志望向け
まずはフルスペック型の東大・京大・東工大・早慶志望の話をしていきます。

MARCH・地方国公立レベルで使っていた
「数学の良問問題集 [Ⅰ+A+Ⅱ+B+C]」・「国公立標準問題集CanPass」
に加えて、
「ハイレベル数学Ⅰ+A+Ⅱ+B+C [ベクトル] 完全攻略」
「ハイレベル数学Ⅲ・C [平面上の直線と複素数平面]完全攻略」
に取り組んでいきましょう。
同時並行か最後に過去問演習を組み込んでいきましょう。
時間がなければ、「国公立標準問題集CanPass」 はカットしてもOKです!
同じレベルの参考書でいうと、「やさしい理系数学」「上級問題精講」があります。
解説の好みで分かれるところですね。
各参考書のおすすめポイント
最初に「ハイレベル数学Ⅰ+A+Ⅱ+B+C [ベクトル] 完全攻略」・「ハイレベル数学Ⅲ・C [平面上の直線と複素数平面]完全攻略」について!
これは問題のレベル自体は非常に高いです。その分、応用問題を戦う術・考え方を教えてくれる参考書です。難しく挫折することもありますが、しっかりやることで応用問題の考え方が身につきます!
東大・京大・東工大・早慶志望はなるべく全部取り組みましょう。
それにより、応用問題がどの分野で出てきても対応できる力が身に付きます!
解説の考え方の部分が特に身につけてほしい部分です。
一旦理解できなくても、期間を空けたり、分かる人に聞いたりして、確実に理解するところまで持っていきたいところです。
▼阪大・東北大・名大向け
東大・京大・東工大・早慶からワンランク下がる阪大・東北大・名大向けの参考書を、さらに得点戦略別に分けていきます!
〇高得点狙いの人

具体的には、入試問題が6問あったときに「良問問題集」の演習のみで解ける問題が数問あります。受験生としては絶対に落とせない問題です。
そして、その中に差をつける一問として「ハイレベル完全攻略」のレベル帯の問題が出題されます。
たとえば、大阪大学であれば、数学に特化して稼いで、英語は苦手だから低めにして逃げ切るという戦略であるとします。そのときは、「ハイレベル完全攻略」に取り組み、数学を武器にして逃げ切りましょう!!
〇数学は確実にタイプ

さらに考え方を鍛えたい人は「世界一わかりやすい阪大の理系数学 合格講座」に取り組むのがおすすめです!
論証が必要な問題とか発想力が問われる問題など考え方を鍛えてくれる一冊になっています。
そのため、阪大志望に限らず、名古屋大学・東北大学等でも応用問題の考え方や、論証問題のアプローチ方法、記述の方法などを身に着けたい人におすすめです!
▼北大・九州大志望の人
最後の旧帝枠である北大・九大についてです!

いわゆる入試の標準的な理系数学の問題が出題されます。
北大であっても、九大の参考書で事足ります。
そして、「ハイレベル完全攻略」は基本的には必要ありません。
そこまで難しい問題は出ないという認識でいて、問題ないです。
出たとしても、受験生間であまり差がつかないため、心配は無用です。
寧ろ、上記の参考書を完成度高く丁寧に仕上げることが非常に大切です!
最後に
ここまで数学の参考書ルートについて説明してきました。
数学は思考力が問われる問題が多く、苦手とする人が多いのは事実です。
しかし、大事なのは「分からなくても諦めない」という気概です!
とにかく手を動かして実験してみることが大切です。
時間的な問題で「答えを見よう」となりがちですが、時間を決めてこの時間は考える、と区切ることが必要です!
そしてできたこと・できなかったことを自分なりにまとめて、成長に繋げていきましょう。
参考動画
今回の参考動画です!また、武田塾神戸湊川校ではルート表について受験相談でより詳しく説明します!
受験相談のお申し込みは下のボタンからどうぞ!
また、武田塾神戸湊川校では
数学以外に他の科目でも解説記事が公開されていますので
是非ご覧ください!
【物理編2024年】
【英語編2024年】
【情報編2024年】
【古文編2024年】
【化学編2024年】



















