こんにちは!
武田塾北久里浜校です!
今回は前回から始まりました参考書シリーズの第二弾!
武田塾の参考書ルートで用いられている基礎レベルの教材について取り上げていこうと思います!
今回はその第二回ということで
7月12日に初版が発行されたばかりの基礎問題精講ⅡB+ベクトルについて見ていきます!
前回はそもそもこの本がどんな参考書かについて紹介・解説を行わせて頂きました.
今回は5訂版との大きな違いである統計分野について,
追加解説、注意点の解説を行っていきます!
基礎問で統計勉強してみたけどよくわからない!といった高校生の疑問を少しでも解消できればと思います!
また,北久里浜校で生徒から出た質問を元に当記事も徐々に改良していきたいと思っていますので
よろしくお願いします!

また,著作権の関係上具体的なページ数や問題番号には触れられませんので,
テーマ毎に紹介・解説を行っていきます.ご了承ください.
テーマ⓪:統計分野の勉強の仕方
統計分野はゴールである推定および仮説検定に向けて必要な道具を取り揃えていくような形で
カリキュラムや教科書がつくられています.
イメージ的には非常に1本道で分かりやすいのですが,
一方でどこかでつまづいたままでは絶対にその後でもっとつまづいてしまいます.
分からない所は必ず解決してから次の範囲に進みましょう.
テーマ①:確率変数と確率分布~確率変数の変換
このテーマでの大きな注意点は特にありません.
少しハイレベルですが,期待値(=平均)や分散についてはデータの分析で定義したものを
確率を用いて同じように定義し直しているだけであると理解できると良いですね.
基本的な内容としては,確率分布表を書き,E(X)を丁寧に計算する.
同様にE(X2)と(E(X))2を計算し,V(X),σ(X)を計算するだけです.
計算練習だと思ってめんどくさがらずにやりましょう.
V(X)= E(X2)-(E(X))2,変数変換による期待値や分散の変換公式については
一度証明を理解した後は暗記で構いません.
ただ,入試問題においてはこれらの公式を証明せよという問題も予想されますので
数学を得点源にしたいMARCH志望以上の生徒については多くの公式を
自分で証明できるようにしておきたい所です.
テーマ②:同時確率分布~確率変数の独立
同時確率分布は最初は表の見方が分からず,
困惑するかもしれませんので教科書などで簡単な例を確認してから取り組むと良いでしょう.
また確率変数の独立については,ちゃんとした定義式を覚える必要はありません.
確率の独立と同様に,”カードを引いて戻さない”という試行を繰り返す場合には
非独立(従属)な試行になるから確率変数も従属であり,
”カードを引いて戻す”という試行を繰り返す場合には
独立な試行になるから確率変数も独立だとイメージで捉えて問題ありません.
また,メタ的な観点から言えば,従属な試行の確率を問題で扱う事はありますが,
従属な確率関数を高校数学範囲で扱う事は極めて困難です.
早慶以上を目指している場合を除き,基本的に確率変数は独立なものであり,
E(XY)=E(X)E(Y)やV(aX+bY)=a2V(X)+b2V(Y)は常に成り立つものと考えてよいでしょう.
(ただし記述式の場合,独立であるから…という一言は必須です)
テーマ③二項分布
独立な確率変数分布の代表的な例として二項分布が知られています.
確率pで起こる試行をn回繰り返すとき,確率分布表が確率の知識から得られ,
そのような分布をB(n,p)と表す訳ですね.
二項分布の期待値と分散は公式として覚える必要があり,
頻繁に使う公式なので必ず頭に入れましょう.
球を取り出す,カードを引く,こんな事にわざわざ名前を付けて何がしたいんだ?
と思うかもしれませんが,
二項分布は,非常に応用性が高く社会の様々な場所に顔を出す非常に重要な確率分布です.
例えば,不良品の発生確率がp,製品をn個作る場合,その不良品の数は二項分布に従います
他にも,ある薬が効く確率をp,被験者の数をnとして二項分布を考えても良いですし,
ある人がある質問にYesと答える確率をp,質問に回答する人数をnとしても良いです.
このような例から二項分布が非常に重要という意識を少しでも持って頂ければ幸いです.
順番が少し前後してしまいますが,
この非常に重要な二項分布は正規分布という非常に取り扱いやすい分布に近似できます.
ここまで勉強すると,世の中のありとあらゆる事が統計的に解析出来ます.
これ以上は文章では表現出来ませんが,統計の世界は非常に奥深く面白いものです.
少しでも興味を持っていただければ幸いです!
テーマ④確率密度関数
確率密度関数の導入は突然でびっくりしますよね.
ここも教科書レベルの参考書に戻ってじっくり理解する事をオススメします.
ポイントは,
今までの確率分布は離散的な確率分布で確率分布表という”表”の形で表現してきましたが,
別の書き方をすればデータの分析で習ったヒストグラムという”図”で表現が出来るという事です
このヒストグラムの一つ一つの棒が面積を表現しているという事まで分かればOKです!
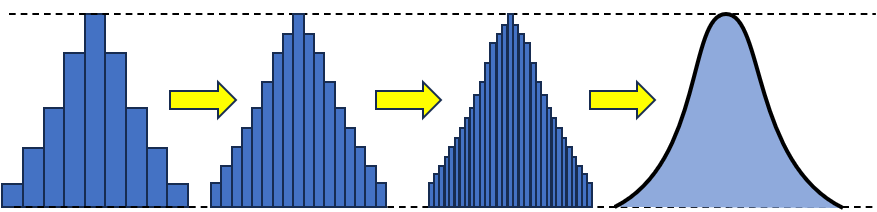
後はデータの数を増し,ヒストグラムの幅をどんどん狭めていきます.
すると下図のようにカクカクのヒストグラムが徐々に滑らかな関数になっていきますね.
このようにして出来た曲線を分布曲線と呼び,
この曲線を表す関数y=f(x)を確率密度関数というだけです.
ヒストグラムで面積が密度だったのですから,確率密度関数でも面積が密度ですね?
関数で面積を求めるなら当然積分ですよね!
テーマ⑤正規分布と二項分布の正規分布近似
正規分布の解説は基礎問に十分な程ありますので,解説はしません.
重要な事だけピックアップして強調しておきます.
①平均m,分散σ2のときの正規分布がN(m,σ2)と表せること
②平均0,分散1のときの正規分布がN(0,1)と表され(ここまでは①から当然ですね),
標準正規分布と呼ばれ、統計学を学ぶ上で最も重要な確率分布である事.
③正規分布に従う任意の確率変数Xが Z=(X-m)/σ と変数変換する事でZがN(0,1)に従う事
④標準正規分布の面積は高校数学では計算出来ないが,計算結果をまとめた標準正規分布表があり,
その表の読み方および表を利用した確率の求め方を理解する事
(赤文字ばかりになってしまいましたが、これほど重要な事が詰まっています!!!)
以上のように,このテーマだけで4つも大事な事があり,
これら全てが高校範囲の統計学の肝であり,問題を解く上でも最も重要です.
何回も読み直し,理解出来なければ簡単な参考書を読む,
周りの先生や友達に聞くなどして120%の理解をしてください.
二項分布の正規分布近似については,
応用性の高い二項分布が綺麗な性質を持つ正規分布に近似できるという極めて嬉しい定理です.
近似出来るという事さえ知っていれば,N(np,np(1-p)) になるのは自明ですね.
分からない場合は二項分布の期待値と分散の公式および正規分布の表し方を見直しましょう.
テーマ⑥標本平均の分布と母平均の推定・母比率の推定
標本平均の期待値を調べていくのですが,ある意味で平均の平均を調べる行為ですから,
最初は混乱するかと思います.
落ち着いて証明を読み一度理解すればその後は公式を暗記して構いません.
更には標本平均の分布もまた正規分布に近似できます.
このとき,標本平均の元となる母集団の分布は二項分布でも正規分布でもなんでも構いません.
「適当な分布から取ってきてもその平均の分布は正規分布になる」
という高校範囲ではなんとも不思議と言わざるを得ません.
証明は大学に入ってすぐに学べますから楽しみにしていましょう.
この定理は中心極限定理と呼ばれ,統計学の根幹を成す2定理の一つです.
(もう一つは大数の法則と言います.興味がある人は調べてみてください)
母平均の推定に関しては標本平均が正規分布に従って分布する事・標準化の式が分かっていれば,
公式はなくても導けるものであると,精講を読んで理解してください.
一度理解した後は推定の式は暗記で構いません.ただ効率よく暗記しましょう.
”母平均は標本平均から少しだけずれた範囲にある”,というのが公式のキモです.
最初は余弦定理や加法定理並みに難しい公式と感じるでしょうが,
それらと同じで慣れてしまえばなんてことはありません.
演習を重ねていく中で徐々に覚えていきましょう.
母比率の推定は母平均の推定がしっかり分かり,何問か演習問題をやってからやりましょう.
母平均の推定公式が理解出来ていれば,
平均を比率に/分散を二項分布の分散に入れ替えただけの簡単な公式と理解出来るはずです.
最後のテーマ仮説検定については,紙面の都合上次回のブログでの紹介・解説とさせてください.
申し訳ございません!
ここまでの内容がしっかり理解できていないと理解出来ない事は間違いないので,
まずはここまでの内容を完璧にしましょう!
以上、武田塾北久里浜校でした!
ここまで読んでくれたあなたも...
こんなお悩みはありませんか?
□ このままの勉強で大学合格できるか不安
□ 独学を進めるための勉強方法が知りたい
□ 勉強に行き詰まっててアドバイス欲しい
□ 今の自分に合う参考書・教材が知りたい
□ 志望大学の対策方法を具体的に知りたい
□ 苦手教科はどうやって克服すればいいか
□ まず何から勉強を始めるのかわからない
□ 将来の進路や志望大学を決めるのに迷う
このような漠然とした不安はありませんか?
このままじゃダメだって余計に焦ったり...。
YouTubeやInstagramで勉強法を調べても、
本当に自分に合う情報かわからなかったり...。
もしあなたが、今そんな悩みを抱えていても
大丈夫です!
これらの悩みはすべて、
無料の受験相談で解決できます!
↓ ↓ ↓
無料の受験相談って何をするの??
…という疑問を持った人のために、
(1)何を話すか
(2)相談の流れ
(3)生徒の感想
をここからお伝えいたしますね。
(1) 受験相談では何を話すか?
武田塾の受験相談は「勉強の相談」を
自由にしていただける場となっています。
例えば、よくある相談は...
・合格勉強プランを作ってほしい
・志望大学の相談に乗ってほしい
・英単語の覚え方を教えてほしい
・大学選びのアドバイスがほしい
・武田塾の仕組みを教えてほしい…など、
受験や勉強の相談ならなんでもOKです!
「入塾の相談」ではなく
「勉強の相談」だからこそ
生徒さま本人のみでお越しいただいてOK。
また、入塾のご希望がなくても大丈夫!
そのかわり...
もし受験相談であなたの悩みが解決したら、
お友達にも勧めてもらえると嬉しいです!
(入塾のご相談ももちろん受け付け中!)
(2) 受験相談はどんな流れか?
① 「無料受験相談」ボタンを押す↓
⑤「受験相談シート」に悩み等を記入
⑥校舎長が悩みを聞いて分析します!
気になることは何でも聞いてください!
⑦課題発見→目標設定→勉強法の提案
完全個別で勉強アドバイスをします!
⑧悩み解決しスッキリした状態で帰宅!
(3) 受験相談をした人の感想
・1日17分を365日続けるだけで、年間100時間の勉強を確保できる話が印象的でした。部活が忙しいことを言い訳にせず、スキマ時間で英単語をがんばります!(高1)
----------------
・学校で使ってる数学問題集の活用法がわからなかったけど、自分の理解度に合わせた使い方を教えてもらえて良かった。(高2)
----------------
・いま自分がやるべきは英語と数学だとわかってすっきりした。(高2)
----------------
・高校では受験情報をあまり話してくれないので、MARCHに合格した先輩たちの時期ごとの勉強内容を知れて刺激になりました。(高3)
----------------
・志望大学と自分の学力のギャップを知ることができました。あてずっぽうな勉強ではなく、目標に向けての勉強をしていきます。(高3)
----------------
・ここからの受験勉強のポイントを少しだけ掴めた気がしました。(高3)
----------------
・自分一人で宅浪して精神的にキツかったので、応援してくれる大人の存在がありがたく感じました。(浪人生)
----------------
(以上、すべて本人承諾済み)
今あなたが抱える悩みを
この機会に解決しませんか?
受験相談にきて悩み解決できると、
「志望大学に合格できる気がする!」と、
勉強のやる気が高まるだけではありません。
今の自分がやるべき勉強がわかるから、
「あとはやるだけ」状態で毎日を過ごせます。
悩みや迷いを抱えたまま過ごす1週間と、
頭も心もスッキリして過ごす1週間では...
勉強内容の吸収力も大きく異なります!
あなたは来週も、
悩みを抱えたまま勉強をしていきますか?
決断するなら、今です!
下にあるボタンから、
ぜひ無料相談を予約してください!
1日でも早くあなたの悩みを解決して、
来週からはスッキリ勉強していきましょう!
↓ ↓ ↓
受験相談に関して
よくあるご質問
(Q) 何曜日の何時なら受験相談が可能か?
北久里浜校は月~金曜は13~22時、日曜は13~20時で開室しています。
その時間内であなたのご希望のお時間をお伝えください。
(Q) 相談に行くときの持ち物はあるか?
過去の模試成績や定期テスト結果など、
成績がわかるものがあると、より具体的なアドバイスができます。
また、あなたが使用している教材について相談したい場合は、
その教材もお持ちいただけると助かります。
(Q) 悩みが漠然としていても大丈夫か?
もちろん大丈夫です。
理想の状態(ゴール)を一緒に思い描き、
現状の課題(スタート)を明確にするため
漠然とした悩みは解決できるはずです。
(Q) 志望校が決まってなくても大丈夫か?
もちろん大丈夫です。
文理選択や学部選択もアドバイス可能です。
どういう方向性を目指すことになっても、
まず基礎固めの勉強が重要になるため、
勉強アドバイスさせていただきます。
(Q) 学力が低くても相談に行っていいか?
もちろん大丈夫です。
今まで難関大に逆転合格していった先輩も、
学力に自信を持ってる人はいませんでした。
一緒に逆転合格を目指しましょう!
(Q) 武田塾を無料体験することはできるか?
1週間の無料体験をすることが可能です。
1対1の個別指導やを自習室を体験できます。
勉強の進め方や、単語の覚え方など、
たった1週間でも勉強姿勢が変わります!
(Q) 入塾する場合の料金はどうなるか?
志望大学や学力によって料金は異なります。
そのため、あなた自身の希望やご家庭の事情を聞かせていただき、
その内容に合わせて料金をお伝えさせていただく流れです。
最後まで読んでくれた
あなたに...
自分の悩みを解決したい気持ちはあるけど、
いきなり「無料の受験相談」に行くのは
まだちょっと抵抗がある、という人には...
Instagramのメッセージ機能で、
いつでも簡単な悩み相談に乗っています!
投稿のコメント欄でもメッセージ機能でも、
いつでもお気軽にご連絡くださいね!
そしてInstagramフォローをしてくれれば、
時期に合わせた合格に近づく情報をお届け!
武田塾 横須賀中央校/北久里浜校の
Instagramアカウントはコチラ
↓ ↓ ↓
https://www.instagram.com/takedajuku_yokosuka
************************************
武田塾 北久里浜校
〒239-0807
神奈川県横須賀市根岸町2-31-2
田中ビル 4階
TEL:046-884-9225
E-mail : kitakurihama@taekeda.tv
************************************










