こんにちは！ 武田塾河内松原校です(^O^)／ 今回は少し脱線して(指数関数)×(三角関数)の形をした積分について書いていこうと思います。 次の問題を皆さんならどのように解くでしょうか。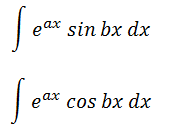 
さて、この問題。 部分積分してみると分かりますが、2回ほど部分積分した後に問題と同じ形をした式が現れます。 そのあとは移項するだけで答えが出てきます。 今回ご紹介したいのはこの問題の別解です。 割と有名なので既に知っている方も多いと思いますので、 「知ってるわ～」 という方は確認程度に見ていただければと思います。 まず、上の二つの式をそれぞれｘで微分しましょう。 微分？ 積分じゃないのか？ と驚くかもしれませんが、とりあえずやってみましょう(^_^)/ 
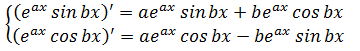この2つの式を使って、右辺をどちらか一方のみが現れる形にします。 
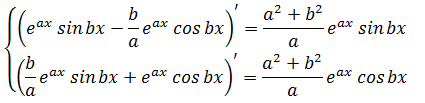答えが見えてきましたね。 この式を整理すると 
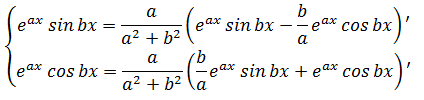となります。 あとは両辺を微分すると・・・ 
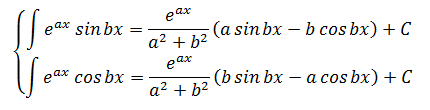答えが出ました＼(^o^)／ この結果を覚えておくとかなり計算速度が上がるのではないでしょうか。 ですがこの結果よりも、結果の導き方のほうが重要ですので、部分積分で求める方法と、今回の方法の両方を覚えておいてください。 武田塾河内松原校では無料受験相談を実施しております。 また、1週間の無料体験特訓も実施しておりますのでご希望の方は下記リンクからお申し込みをお願いいたします。
