こんにちは！ 武田塾河内松原校です(｀・ω・´) 今回は三角関数の定積分について書いていこうと思います。 前回に引き続き、特殊な置換をする解き方を紹介するのですが、これを使えばほぼ全ての三角関数の積分が可能になります。 ～三角関数の積分～ ① tanx = t とおく。 ② tan(x/2) = t とおく。 さっそく説明していきます。 ① tanx = t とおく これは被積分関数が(sinx)^2, (cosx)^2, tanxを含んでいる際に使う方法です。 tanx = tと置換することで、(sinx)^2と(cosx)^2をtで表すことが出来ます。 実際にやってみましょう。 1 + (tanx)^2 = 1/(cosx)^2 より 1 + t^2 = 1/(cosx)^2 (cosx)^2 = 1/(1+t^2) 1 - (sinx)^2 = (cosx)^2 より (sinx)^2 = t^2/(1+t^2) この結果を使って被積分関数をtの関数として表し、積分していきます。 ② tan(x/2) = t とおく これは被積分関数がsinx, cox, tanx を含む際に使う方法です。 ①の時と同じく、 tanx/2 = tと置換することで、sinx, cosx をtで表すことが出来ます。 実際にやってみましょう。 二倍角の公式より tanx = tan(2×x/2) = 2tan(x/2) / 1 - (tan(x/2))^2 = 2t/(1-t^2) 二倍角の公式より cosx =cos(2×x/2) = 2(cos(x/2))^2 - 1 1 + (tanx)^2 = 1/(cosx)^2 より cosx = 2 × (1/1+(tan(x/2))^2) - 1 = 2/(1+t^2) - 1 = (1 - t^2) / (1+t^2) sinx = cosxtanx = 2t/(1+t^2) この結果を使って被積分関数をtの関数として表し、積分していきます。 三角関数の積分であればほぼ全て①か②の方法で解くことが出来ます。 一度解いてみましょう。 今回は例題に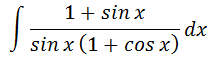 
を使います。 この問題の場合、②の方法が有効ですね。 t = tan(x/2)とおくと、dx = (2/(1+t^2))dt 
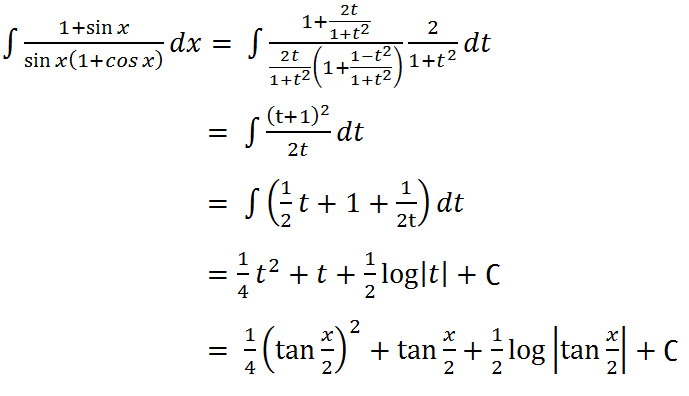小さくて見えにくいと思いますが、私の編集能力ではこれが限界でした(>_<) さて。 上記の方法で解いた方は気づくと思いますが、この方法。 非常に時間がかかります(^-^; 他の方法を使った方が速く解くことが出来ます。 どうしても解けないときの最終手段として使ってみてくださいね。 武田塾河内松原校では無料受験相談を実施しております。 また、1週間の無料体験特訓も実施しておりますのでご希望の方は下記リンクからお申し込みをお願いいたします。
