こんにちは！ 武田塾河内松原校です(^^) 前回に引き続き特殊な解き方をする定積分について書いていこうと思います(｀・ω・´) 今回は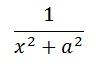 
の含む定積分の解き方を紹介します！ この型の問題の解き方は２種類あります。 ① x = atanθとおいて計算 ②逆正接関数を使って解く それでは一つずつ解き方を見ていきましょう。 今回は 
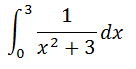を例にします。 ① x = atanθとおいて計算する これが最も基本的な解き方です。 ②の解き方ができない人はこの方法一択となるでしょう。 実際に解いてみましょう。 x = √3tanθ とおく。 dx = √3/((cosθ)^2)dθ (与式)= ∫[ 0..π/3]{1/(3(tanθ+1)) × √3/((cosθ)^2)dθ = ∫[0..π/ 3] √3/3 dθ = √3π/9 このようにして、定積分を求めることが出来ます。 置換後の計算もすっきりしていて解きやすいですね(^^) ②逆正接関数を使って解く この方法は前回に引き続き三角関数の逆関数を用いた公式に当てはめて解く方法です。 知らない人は無視してもらって構いません。 
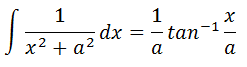このような公式があります。これを使って計算してみます。 (与式) = [(1/√3)arctan(x/√3)] (x=0 → 3) = (1/√3)arctan√3 = √3π/9 計算量が少なくて、楽に感じます(^^) ②の解き方ができる人は積極的に使ってもらえればなと思います。 相変わらず計算部分が読みづらくなっていると思いますがご容赦ください(-_-) 分からない部分があれば直接聞きに来てくださいね！ 武田塾河内松原校では無料受験相談を実施しております。 また、1週間の無料体験特訓も実施しておりますのでご希望の方は下記リンクからお申し込みをお願いいたします。
