こんにちは！ 武田塾河内松原校です(・ω・)ノ 今回は区分求積法について書いていこうと思います。 人によって得手不得手が分かれる分野かと思いますが、今回は教科書に載っている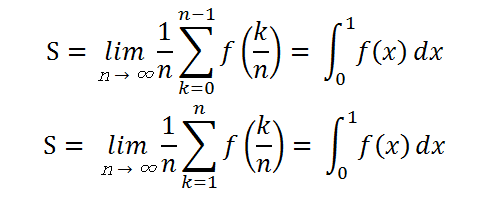 
この2つの公式について解説したいと思います。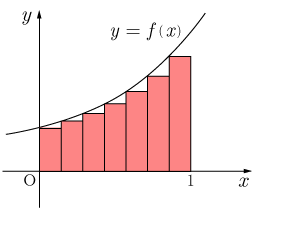 
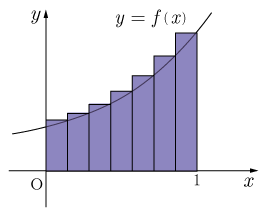これから曲線で囲まれた図形の面積を求めるわけですが 分かりやすいように上の方の公式を公式①、下の方を公式②とし、同様に上の方の図を図①、下の方を図②とします。 公式①が図①に、公式②が図②にそれぞれ対応しています。 公式はどちらも「図の長方形の幅を限りなく0に近づければ正確な面積になる」ということを表しています。 実際に計算してみましょう。 まずは公式①から考えていきます。 図①はｘ＝0からｘ＝1までの区間をn等分して、長方形の左端を関数y = f(x)に合わせています。 x = 0 から x = 1 までの区間をn等分するので、一つの長方形の幅は n/1 となります。 各長方形の高さは左端から順に f(0/n), f(1/n), ・・・・・・f(n-1/n) となります。 よって長方形の面積の和は 
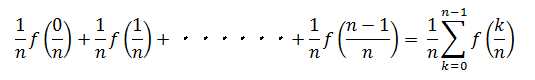となります。 図①を見てわかるように、求めた長方形の面積の和は実際の面積より若干小さいです。 ここで、n→∞として、長方形の幅を限りなく0に近づけた時の面積の和をＳとすると、Ｓは
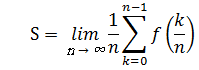となります。 nを無限大にすることで、実際の面積との差が限りなく0に近づくのです。 公式②についても同様に考えられます。 公式①と異なる点は長方形の右端を関数 y = f(x) に合わせるということです。 ですから、長方形の高さは左から順に f(1/n), f(2/n), ・・・・・・f(n/n) となります。 よって、長方形の面積の和は 
となります。 図②を見てわかるように、求めた長方形の面積の和は実際の面積より若干大きくなります。 ここで、n→∞として、長方形の幅を限りなく0に近づけた時の面積の和をＳとすると、Ｓは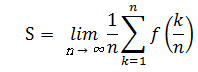 
となります。 こちらも公式①と同様に、nを無限大にすることで、実際の面積との差が限りなく0に近づきます。 さて、２通りの求め方を説明しましたが 公式①と公式②の計算結果は等しくなります。 実際に計算して確認してみてください。 後はなぜ∑の式が積分の式で表されるのか、ということですが、 単にわかりやすいように書き直したに過ぎません。 k/n→x 1/n→dx とすると、f(x)dx は幅のとても小さな長方形の面積を表すことになります。 さらに、lim[n→∞]∑[k=1..n] → ∫[x=0..1] (どちらもx=0→1まで足していくという意味) と置き換えることで 
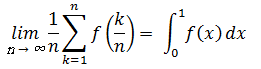と表されるようになるのです。 いかがでしょうか？ 慣れない数式の表記で少し分かりづらくなってしまっているかもしれませんが、理解の手助けになれば幸いです。 武田塾河内松原校では無料受験相談を実施しております。 また、1週間の無料体験特訓も実施しておりますのでご希望の方は下記リンクからお申し込みをお願いいたします。
