こんにちは!
武田塾河内松原校です(・ω・)ノ
皆さん、積分してますかっ!?
数Ⅲの積分はこまめに解いておかないと、勘が鈍ってしまいます。
特にセンター試験後は勘を取り戻せるようにたくさん解かないと、2次試験で苦労するのでご注意を!
数Ⅲには積分を利用した様々な応用問題がありますね。
例えば、区分求積法、積分方程式、微分方程式、曲線の長さ、面積、体積などなど・・・
大変ですね(-_-)
さすがに一つの記事では書ききれないので、今回は体積について書いていこうと思います!
体積の問題は大きく分けて、「回転体の体積」と「非回転体の体積」の問題があります。
①回転体の体積
回転体の体積の問題は
1.回転体の公式を使って解く。
これだけで多くの問題はできてしまいます。
後は積分するのみ・・・!
しかし、難しいのはこの後の計算ですよね(´・ω・`)
回転の軸が斜めだったり、場合分けが必要だったり・・・
実は計算を楽にする方法があります!
「バウムクーヘン分割」や、「極座標を使って体積を求める」
といった求め方をご存知ですか?
これらの公式を使えば、ややこしい計算をしなくても一発で答えが出てしまいます( ゚Д゚)
もはや反則技ですね(笑)
実際、入試でそれらの公式を使うには面倒な証明を行う必要があるので、あくまで使うのは計算用紙の上のみにしてくださいね(^-^;
しかし、普段から裏技公式に頼ってばかりでは実力は身につきません。
普段は正規の方法で解いて、確認程度に使うようにしてください。
②非回転体の体積
非回転体の体積は
1.どの平面に沿って切断するか決める。
2.平面に沿って切った断面積を求める。
3.積分!
の3ステップでだいたいの問題は解けます。
体積が苦手な人はまずステップ1で迷ってしまうのではないでしょうか。
実のところ、どの平面で切ろうと答えにたどり着くことはほとんど可能です。
ただし問題によって、切断すると断面積が容易に求められる平面とそうでないもの、最悪求められないものが存在します。
つまり、どの軸に垂直な平面で切るのかが一番重要なポイントなのです( ゚Д゚)
例えばこの問題。
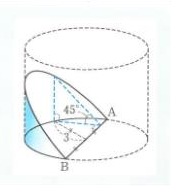
この円柱を曲線によって隔てられた立体のうち、小さいほうの体積を求めるとします。
定番の問題ですね(笑)
この体積を求めるのに、どの平面で切れば一番楽に解けるでしょうか?
答えはY軸に垂直な平面です。(y=tで切断)
切断面が二等辺三角形になるので、容易に解くことができます。
逆に最も解きにくくなってしまうのは、Z軸に垂直な平面で切ることです。(z=tで切断)
切断面が円の一部となり、2~3倍くらい面倒になってしまいます。
では、どうすれば最適な切断面を見つけられるのか?
ぶっちゃけ経験則です(^-^;
場数を踏むことで、次第に「ここで切れば断面がこうなるな」と考えられるようになります。
たくさん問題を解いて、「この平面で切ればこういう断面になるな」
と想像できるようになる頃には体積はマスターできていることでしょう。
もう一つ、非回転体の中には不等式で表された立体の体積を求める問題があります。
例えばこんな問題。

非回転体の体積と同様に、いずれかの平面で切断して積分することで体積は求められます。
この問題でも最も重要なポイントは、どの軸に垂直な平面で切るのかということです。
このような問題の場合、切り口が最も単純な図形になる軸の選び方が決まっており、
「次数が多い文字」「出現回数の多い文字」の軸を選ぶと良いです。
この問題の場合、y=tとすれば一番簡単になります。
要は、一番鬱陶しい文字を定数扱いにしてやれば良いのです。
この形式の問題を見て、立体の形を必死にイメージして解こうとする人がいますが、間違った立体の形をイメージしている場合が多いです。
ただ単純にいずれかの平面で切断して積分すればよいのです。
いかかでしたでしょうか?
体積に悩む皆さんの助けになれば幸いです。
上記の裏技公式に興味がある方はぜひ直接聞きに来てください!
先ほど計算用紙の上でのみ使うように言いましたが、実は「ここまでなら使える」というラインが存在します。
直接聞きに来てもらえれば、入試でどの程度まで裏技公式を使ってよいのか等も含めて教えます(笑)
武田塾河内松原校では無料受験相談を実施しております。
また、1週間の無料体験特訓も実施しておりますのでご希望の方は下記リンクからお申し込みをお願いいたします。













