受験生のみなさんこんにちは、武田塾春日井校です。
夏休みも終わってしまいましたが、
みなさんの受験勉強の進捗状況はどうなっているでしょう。
以前に立てた計画に則り順調にきている科目もあれば、
計画よりも大分遅れをとってしまった特定の科目もあると思います。
本日はその以前立てた計画よりも遅れをとってしまった数学にフォーカスして、
今後の共通テストまでの勉強法について詳しくお伝えしていきます。

共通テストまでに数学の基礎を最短で仕上げていくために最適な勉強法
数学が苦手!でも、志望校受験には必要な人向け
数学に苦手意識があって、本当に自分から勉強することが大変という人に提案になります。
実をいう私も大の数学苦手、今でも数学には手を焼いています。
そんな数学苦手な人たちにまず提案です。

本当にその志望校でないといけないでしょうか。
私の場合も、志望校をかえてしまった中のひとりです。
志望校をかえてもあなたが学びたい学部に進学可能な選択肢があるのであれば、
まず数学が受験科目にない大学の学部を調べてみましょう。
特に経済学部等の中、国立大の条件では数学外しは困難ですが、
「公立大(いわゆ県立)の中には、数学を除いても受験可能」です。
という貴重な大学がみつかるここともあります。
まずは探してみましょう!
それでも数学の勉強をすすめていく人に
数学の勉強は苦手にしていて、それでも数学の勉強を続けていく必要のある人のために、
これからの数学勉強法と最適な参考書の紹介を一緒にしていきます。
共通テストまでの先を見越した勉強法
共通テスト数学の問題は、数学ⅠAにしてもⅡBにしても基礎的な問題であるとされています。
実際過去問を見てみることが一番の早道であることは確かです。

共通テストの大問は、分野ごとに分けられて出題されていますから、
まず自分が大問の必須の問題を含め、選択問題はどの分野を選ぶのかを確認します。
その後、まず共通テスト過去問を大問ごとに見て、実際解いてみてください。
今の実力で解ける問題と解けない問題とに区別します。
解けない問題がわかったところからが今回の勉強法になります。
ここからは共通テスト問題を見ていきます。

【第2問】図形と計量についての分析ができるかどうか
共通テスト問題の大問2の分析をまずは行ってください。
自分で自信がないなと思った人は、遠慮なく大手予備校の分析を読み、活用していきましょう。

問題分析の例1:図形と計量から
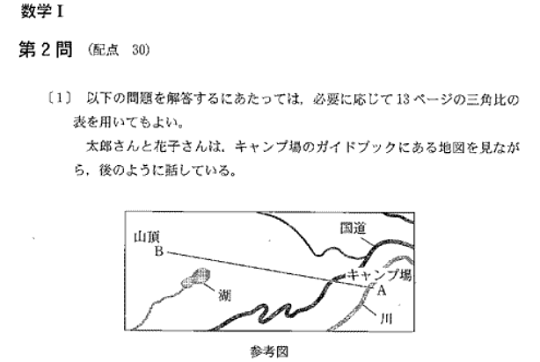
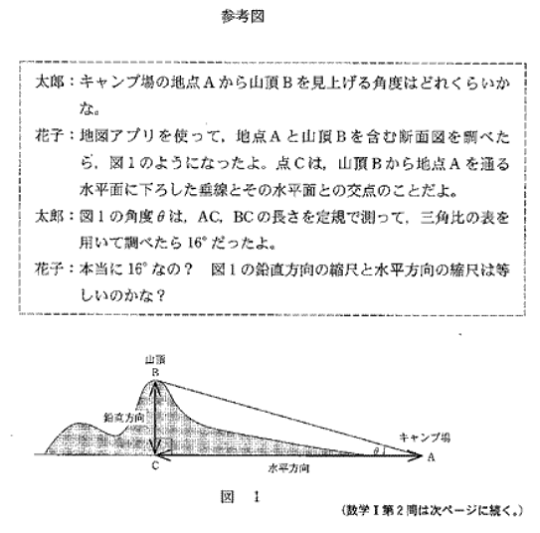
太郎さんと花子さんがキャンプ場で見上げた山についての仰角がテーマの問題で、
水平方向と鉛直方向の縮尺の違いを修正して、正しい仰角の情報を求める。
三角比の表を利用する問題。
問題分析の例2:図形と計量から
外接円の半径が与えられた三角形についての問題であり、正弦定理を利用する。
基本計算が多いが、(2)で辺の長さのとり得る値の範囲を調べる際に、
円の直径で制限がかかることに気づかなければ解きにくい。
上記が問題分析の例になります。
ここで止まってしまっていると勉強にはなりません。
予備校の大問ごとの分析結果をよく読んだ後で、
今後はその大問2に対しての自己解答力の分析を行います。

問題側からの分析だけではなく、自己の現在の解答力の分析ができたところが勉強のはじまりです。
「三角比」や「正弦定理」といった数学の用語が分析の中に入ってきています。
まず、自分が「三角比」、「正弦定理」を利用して解答していく問題であることに気づくことができているかの判断と、
実際、「三角比」、「正弦定理」についての基本的な知識を身につけていたのかどうか自己分析してください。
自己分析後には適した参考書に従う
問題の分析、自己の解答力の分析がととのったら
次にやることは現在の自分に合う参考書で勉強することです。

1分1秒をあらそう受験勉強に無駄な時間を割くことはできません。
武田塾からは具体的な提案をします。
1.基礎問題精講シリーズ
2.初めから始める数学
3.数学大全
4.(やさしい高校数学シリーズ)
上記4冊を使って勉強することをお勧めします。
三角比の定義による違い
共通問題に関するところで、三角比に関連する問題を例にしていましたので、
それぞれの参考書の違いについて理解を深めるために「三角比の定義」を使っていきましょう。
1.基礎問題精講から
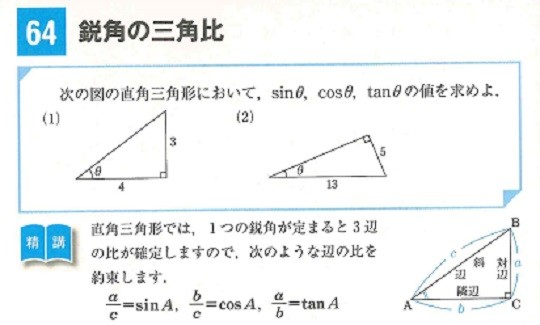
基礎問題精講の場合には、「三角比」についての説明はとても簡潔に行われています。
直角三角形では、1つの鋭角が定まると3辺の比が確定しますので、上記のような辺の比を約束します。
との表現があるだけです。
この表現の簡潔さから言っても、基礎問題精講だけを使って勉強が勧められる人というのは、
「三角比」が何であるかをしっかり理解できていている人です。
その基本的理解事項を入試で出題されるレベルの問題で
どんどん実践することが必要な人に使っていって欲しい参考書です。

初めから始める数学Ⅰから
「初めから始める数学Ⅰ」はまず「三角比」の定義から入っています。
〇三角比を直角三角形で定義しよう!
「三角比って、何?」と思ってるかも知れないね。この「三角比」とは文字通り、「直角三角形の辺の比」のことなんだ。
図1のように、3辺の長さがa,b,cと与えられたとしよう。このとき、この直角三角形の直角ではない、2つの内角の和の1つをθとおくよ。
この角度θ(0°<θ<90°)に対して、3つの三角比:sin θ(サインシータ)、cos(コサインシータ)、tanθ(タンジェントシータ)を定義する。
日本語でも呼び方があり、sin(サイン)を「正弦」、cos(コサイン)を「余弦」、tan(タンジェント)を「正接」と呼ぶんだよ。
:「初めから始める数学Ⅰ(改訂3)より」
「初めから始める数学シリーズ」の特徴は本当に初学者向けの参考書だということ。
語りかけの形式で違和感なく学習に入りやすい表現になっています。
「数学ⅠA基本大全」から
「数学ⅠA基本大全」も初学者、あるいは基本の理解ができていない人向けの参考書になります。
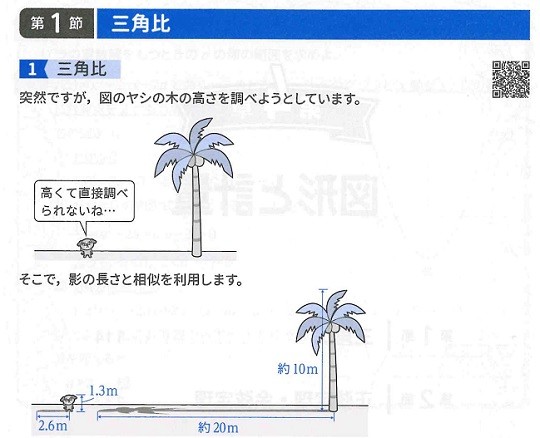
「三角比」についての基本的な理解を促すために、上記のような入りになっています。
そしてその説明ですが、
上の図のように背の高さ1.3m犬の影が2.6mのとき、背の高さと影の長さの比が
1.3:2.6=1:2になっています。なので、ヤシの木の影の長さが約20mであれば、ヤシの木の高さが約10mであるとわかります。
しかし、自分の背の高さと影の長さの比を調べて、さらにヤシの木の影の長さを調べるのは大変です。そこでヤシの木の影の長さと、ヤシの木のてっぺんを見上げた角(仰角といいます)からヤシの木の高さを求める方法を使います。
:「数学ⅠA基本大全」から
まとめ
本日は、数学の勉強が遅れてしまっている人が、
その遅れをどうやって解消していくのかについて、
具体的な参考書名をあげてお伝えしてきました。
今回ご紹介したのは共通テストまでです。
何とか基礎力の補充を行えば、数学を苦手にしている人でも平均点ぐらいには点数を伸ばせるものと考えています。
9月には入りましたが、焦る気持ちを抑えて勉強に取り組んでいきましょう。
無料で武田塾の勉強法を学べる!
武田塾では「無料受験相談」を実施しております。
・志望校に逆転合格する勉強法
・あなたにぴったりの参考書紹介
・武田塾の詳細や料金説明 など
入塾義務はございませんので、
まずはお気軽にお近くの武田塾までお問合せください。
-------------------------------------------------------
春日井の塾、予備校なら
日本初!”授業をしない”
武田塾春日井校
〒486-0945
愛知県春日井市勝川町7丁目35
LIPRO勝川 3階北側
TEL:0568-37-2982











