「共通テストで数学が難化すると聞いたけど、どう対策したらいいかわからない」
「問題の内容が変わるらしいし、難関大を目指すのにこのままの勉強法でいいのか不安」
この記事はそんな方へ向けて書いています。
こんにちは!
金沢駅より徒歩5分、大学受験予備校・個別指導塾の「武田塾 金沢校」校舎長の酒見です。
先日、共通テストの数学の特徴や変更点に関する記事を書きました。
→ 【勉強法】5分でわかる!共通テストの数学!特徴や変更点を解説!
そこで今回は、共通テストの特徴や変更点を踏まえて「どのように勉強すればよいか」を解説します!
これを読めば、今日からどのように勉強すればいいかがわかり、共通テストへの不安が解消できます!
また、武田塾らしくおすすめの参考書も紹介するので、教材選びも迷う必要はなくなります!
問題の種類ごとに勉強法を徹底解説するので、ぜひ実践し "伸びる" 勉強法を身につけてください!
それでは早速どうぞ!
目次
2.【詳しく】「数学を活用する力」とはどういうことか?
2-1. 定義を正しく理解し、幅広く数式などを扱える力
2-2. 日常の場面で数学を使える力
2-3. 未知の事象を数学で探究できる力
3.【徹底解説】共通テストを踏まえた数学の難関大対策や勉強法!
3-1. 定義を正しく理解し、幅広く数式などを扱えるようになるために
3-2. 日常の場面で数学を使えるようになるために
3-3. 未知の事象を数学で探究できるようになるために
1.【おさらい】共通テストの数学!特徴や変更点!

前回の記事 【勉強法】5分でわかる!共通テストの数学!特徴や変更点を解説! で書いた共通テストの数学の特徴や変更点は次の2点です。
|
|
① 数学Ⅰ・A の試験時間が70分に増加!
従来と比べて、数学Ⅰ・Aの試験時間が増加しました。
| 数学Ⅰ・A | 数学Ⅱ・B | |
| センター試験 | 60分 | 60分 |
| 共通テスト | 70分 | 60分 |
② 知識だけでは解けなくなり、数学を活用する力に重点がおかれる!
前回の記事では数学B・ベクトルについて分析し、次の4つの力が試されると伝えました。
|
|
では、ベクトル以外の数学全体として「数学を活用する力」とはどのようなものでしょうか。
これがわかれば対策も打てるので、詳しく掘り下げていきます。
2.【詳しく】「数学を活用する力」とはどういうことか?
プレテストを参考にすると、主に次の3つの力が必要だとわかります。
|
|
具体的に、プレテストを参考に解説します。
2-1. 定義を正しく理解し、幅広く数式などを扱える力
数学Ⅱ・Bの第1問を参考に解説します。
【参考】平成30年度試行調査 数学Ⅱ・B 問題 第1問 [1](2)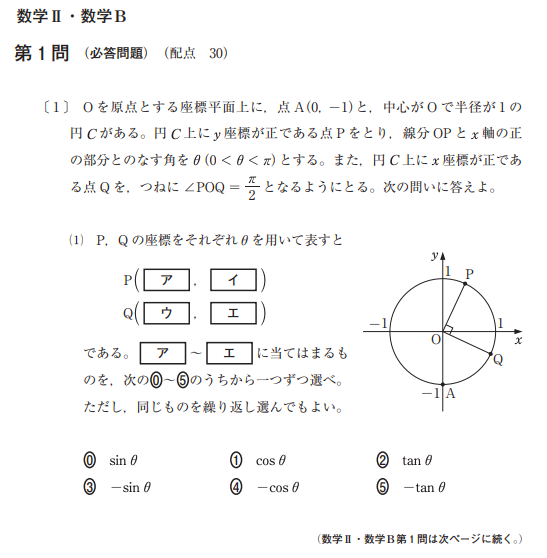
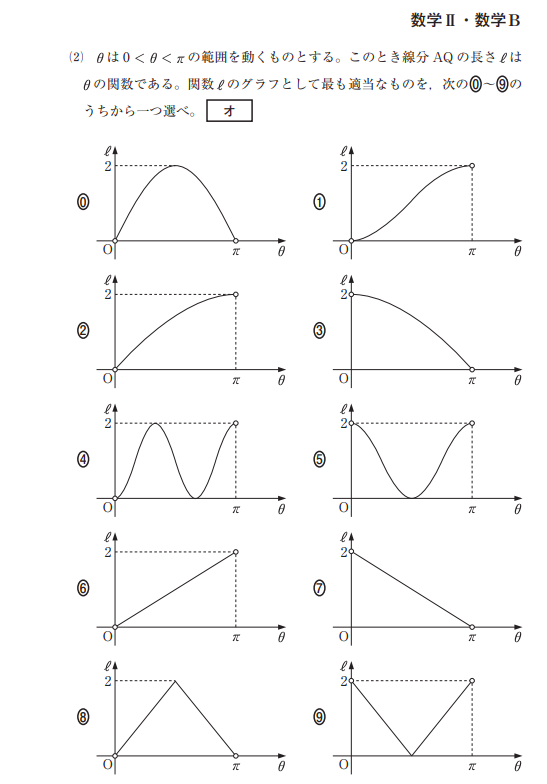
解答は②ですが、このグラフは実は書き方を習いません。
求める長さは![]()
だとわかるのですが、三角比と根号( √ )が混ざった関数の書き方は習いません。
だからこの問は、根号の特徴や、根号の中の関数の形を的確に捉えなければいけません。
考え方としては、
① cosのグラフを描く
② cosにマイナスがついてるので①を上下反転する
③ ②に1/2を加えるので、②のグラフを上方に1/2ずらす
④ √ はグラフ的には高さが変わっても反転はないので、伸び縮みしたグラフを選ぶ
というように、根号の中の式や記号の意味とグラフの変化を順番に整理して、解答が得られます。
また、なかなか出題のなかった軌跡も出題されたので、的を絞って対策するのは難しそうです。
したがって、定義を正しく理解し、幅広く数式などを扱える力が必要になります。
2-2. 日常の場面で数学を使える力
数学Ⅰ・A 第1問を参考に解説します。
【参考】平成30年度試行調査 数学Ⅰ・A 第1問(2)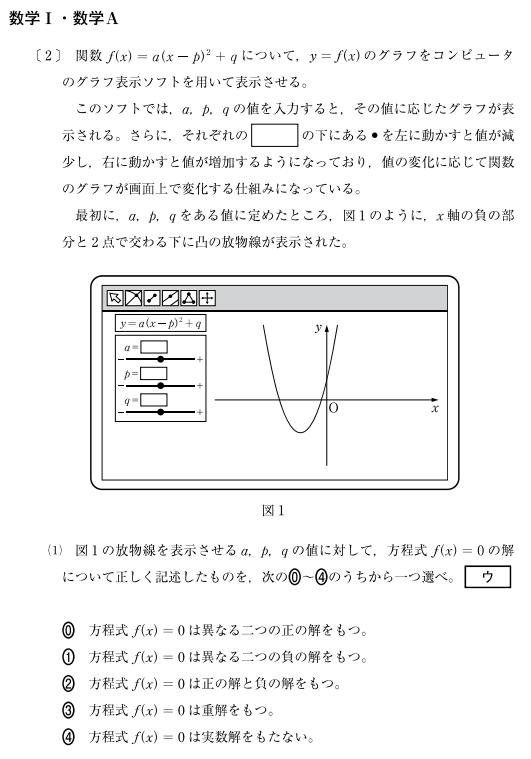
この問では、コンピュータソフトと思われる画面で関数を操作するという状況設定がされています。
だから、問に入る前の導入や情報整理が長くなっています。
日常の場面で数学を使えるためには、多くの情報を的確にすばやく整理する能力が必要です。
2-3. 未知の事象を数学で探究できる力
数学Ⅱ・Bの第1問を参考に解説します。
【参考】平成30年度試行調査 数学Ⅱ・B 問題 第1問 [3](2)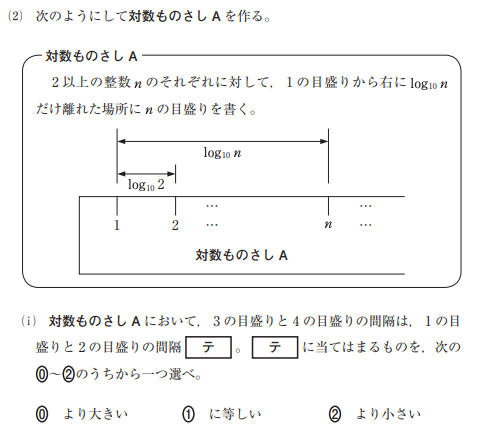
「対数ものさし」という物が登場しました。
教科書はもちろん、いかなる参考書にもこのような物は載っていません。
問自体は特別難しいわけではありませんが、このように未知の物や考え方を扱う問が登場します。
しかし数学の知識と活用力があれば解ける問題になっていて、未知の事象を数学で探究できる力が試されています。
3.【徹底解説】共通テストを踏まえた数学の難関大対策や勉強法!
「数学を活用できる力」をつけるため、具体的な対策や勉強法を徹底解説します。
勉強に用いる参考書も紹介します!
3-1. 定義を正しく理解し、幅広く数式などを扱えるようになるために
定義を正しく理解し、幅広く数式などを扱えるようになるためには、定義やあらゆる数式の使い方をたくさん学ぶことが有効です。
具体的には2ステップの勉強をしましょう。
① 定義を正しく「覚える」
まずは定義を正しく「覚えて」、スラスラ説明できるようになりましょう。
たとえば、「√a 」を正しく説明すると、
"2乗してaになる数のうち、正の方"
となります。
(中学3年の学習要領ですが、ただしく説明できるかな?)
定義を正しく「覚える」ことで、問題を正しく認識できるようになります。
② 数式の使い方をたくさん学ぶ
数式の使い方は1つではありません。
数式の様々な使い方を数式ごとにまとめると良いでしょう。
たとえば、sin(三角比)であれば、
・加法定理などの三角関数としての使い方
・斜辺から高さを求める使い方
というように、その数式をどのように使えるのかをまとめておきましょう。
定義と数式の使い方は『基礎問題精講』シリーズ
このように定義やあらゆる数式の使い方をたくさん学ぶためには基礎問題精講がおすすめです!
あらゆる入試問題を解くための基礎的な問題が網羅されており、定義や数式の使い方、解法などを幅広く身につけることができます。
数学の偏差値が70程度の生徒さんでも「これ忘れとった!」と言うことがあるので、できる人でも意外と穴があることに気付けます。
入試の基礎だからこそ、基礎問題精講は問題と解法を暗唱できるくらい繰り返すとよいでしょう。
【新課程】数学IA・IIB・IIIC基礎問題精講四訂版
3-2. 日常の場面で数学を使えるようになるために
前項で触れましたが、日常の場面で数学を使えるためには、多くの情報を的確にすばやく整理する能力が必要ということです。
情報を早く正確に読み取れるようにするために、短い文章の問題から徐々に長い文章に慣れるよう演習量を重ねましょう。
多くの情報を的確にすばやく整理する能力をつけるためには『チャート』系+実践問題集系
基礎問題精講レベルの問題ができるようになったら、扱う条件を多くしたり、少しずつ長い文章に触れるためチャート系を使いましょう。
特に青チャートだと難易度としては共通テストも十分に解けるようになるのでおすすめです。
チャート式基礎からの数学(青チャート) 数Ⅰ+A 新課程
また、チャート系を終えたら、実践問題集や入試過去問等でさらに長い文章の問題を扱えるようにしましょう。
3-3. 未知の事象を数学で探究できるようになるために
未知の事象を数学で探究できるようになるためには、初見の問題を見て解法の方針を考える練習をたくさんすることがおすすめです。
実際に解かなくても、問題を見て、解くために必要な条件が何か、そしてその条件を使って何を求められるか「解法の方針」を立てる勉強をしましょう。
未知の事象を数学で探究できるようになるためには『良問プラチカ』
良問プラチカは標準〜発展レベルの問題が厳選して掲載されていて、2次試験対策まで使える参考書です。
シリーズは文系Ⅰ・A・Ⅱ・B、理系Ⅰ・A・Ⅱ・B、理系Ⅲの三種類あるのですが、Ⅰ・A・Ⅱ・Bレベルでは
理系 < 文系
となっているので注意しましょう。
プラチカをバッチリ解けるレベルならどのような未知の問題でも対応できますので、ぜひ演習前最後の1冊でプラチカに取り組んでみてください!
文系数学の良問プラチカ 数学Ⅰ・A・Ⅱ・B
4. まとめ
いかがだったでしょうか?
情報量が多いので、自分のレベルに合うものから少しずつやってみてください。
また、ここで紹介したやり方の他にも、共通テスト形式の模試をいくつか受けてみて、予想される形式に慣れていくことも、共通テストを突破する上で良いと思います。
共通テストはセンター試験に比べ難易度が上がり、初めての形式に戸惑うこともあると思います。
しかし、必要な情報を身に付け、正しい勉強法を実践してもらえれば、必ず成果は出ると思います。
いつも伝えていますが、これを見てくれた、勉強に前向きな君だからこそ、しっかり実践し身に付け合格を手にしてほしいと思います。
無料受験相談お申し込み受付中!
気軽にチャットで相談したい方はぜひ公式LINEでお声かけください♪
















