「京都教育大学ってどんな大学??」
「京都教育大学の数学って、どう対策したらいい?」
「現時点で合格圏外、E判定でも京都教育大学に合格する方法を教えてほしい!」
この記事はそんな方へ向けて書いています。
はじめまして。
「E判定、合格はできないよ」と言われた数々の生徒を
逆転合格へと導いてきました武田塾JR奈良校です。
武田塾では、日本で出版されている全ての参考書を分析し、
京都教育大学の過去問分析を積み重ねて、
たくさんの生徒と共に、逆転合格を掴み取ってきました。
本記事では、
京都教育大学の数学対策についてご紹介いたします!
あなたの京都教育大学合格への一助となれば幸いです。

JR奈良校では自学自習の徹底管理・サポートを行い、
早稲田、関関同立、旧帝大、医学部医学科など数々の合格者を輩出しています!
詳細はこちらをご覧ください↓
3科目偏差値39から半年で立命館大学文学部(偏差値57.5)合格!偏差値18.5UP
英語偏差値40から半年で東京理科大学理工学部(偏差値60.0)に合格!
2ヶ月で模試総合点71点アップ!大阪大学工学部(偏差値62.5)に合格!
・2ヶ月で模試5教科660点→731点!大阪大学工学部に合格!
ホームページからのお問合せ・受験相談をお申し込みの方は、
こちらから申し込みください↓
目 次
京都教育大学の数学ってどんな問題?
合格点を取るための具体的な勉強法をそれぞれの分野で紹介!
揺るぎのない基礎力を!
国公立は記述力勝負!おすすめの参考書は?
仕上げに過去問演習!そのポイントとは?
京都教育大学の数学 過去問の傾向
京都教育大学の2次試験数学は、教育学部の中でも数学領域専攻、理科領域専攻の前期試験で必須科目(並びに技術領域専攻の選択科目)となります。
問題パッケージは大問5題構成で、すべて記述式となっております。
大問5は例年選択問題になっていて、数学領域専攻の方は数Ⅲ範囲が含まれる大問を、理科領域専攻・技術領域専攻の方は数Ⅲの内容を含まない問題との選択が可能となっています。
これらを120分で解きます。
十分に考える時間はありますが、どれもそれなりの記述が必要となりますし、作図や図示などを迫られる問題も多くなかなか慌て気味の試験となることでしょう。
また、出題ムードには教育大学独特の雰囲気があり、数学の腕に覚えがある受験生でも、何度か過去問で練習しておかないと痛い目に遭う可能性がある出題となっています。
以下の表は、最近4年分の過去問について、その出題実績をまとめたものです。
詳しく見ていきましょう。
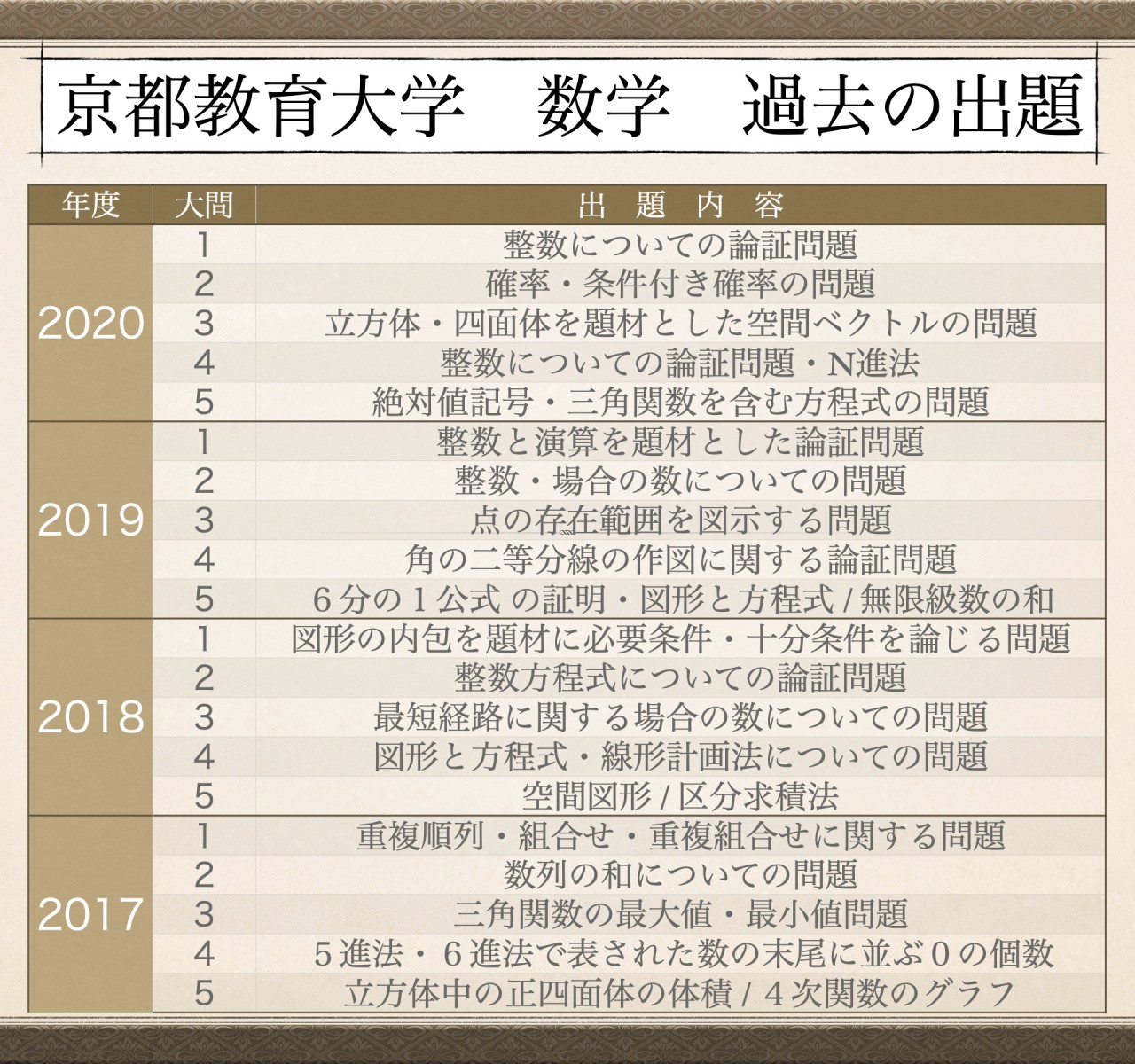
ひと目見て分かる特徴として「論証問題が多い」ということが分かります。
また、論証を要求される内容も、普段日常的に行っている式変形についての必要条件や十分条件を問う「そもそも」の問題であったり、ある枠の中にある図形を詰め込むときの条件を問うものであったりなど、なかなか普通の問題集では見かけないような設問に向かっていかなくてはなりません。
基礎的な数学の力はもとより、一般的な国公立大学で課せられる問題に対する記述対策のほか、この大学の過去問に取り組むことで効果的に伸ばせる力が必要です。
以下で、具体的な対策を紹介します。
【より上位の大学へ!武田塾JR奈良校での成績アップ&逆転合格事例!】
偏差値40から半年で東京理科大へ逆転合格!その勉強法の秘密とは?
【立命館】9月3教科偏差値39からの逆転合格劇 奈良育英高校再受験生
3ヶ月で3科偏差値10アップ!数学・英語の勉強法【南陽高校1年】
京都教育大学 数学の対策・勉強法
高校数学を基礎からコツコツと身につけて、最終的には京都教育大学合格レベルに達するための勉強法を紹介します!
まずは典型問題の解法を身につける
最終的に京都教育大学の問題を解けるようになるためには、第一に基礎となる典型問題の解法を身につけておかないといけません。
模試や過去問で登場する応用問題も、基本的には典型問題で使う考え方が集まったものであり、解答の各ステップの中で「必要な手続き(式変形やグラフの書き方、各値を求める公式など)を知っている」から解けるのです。
まずはこの「必要な手続き」というのを覚えていきましょう。
数学の基礎を押さえるのに様々な参考書・問題集がありますが、1番のおすすめはこの『基礎問題精講』シリーズです。
このシリーズで、典型問題を手広く効率よく学んでいきましょう。
『チャート式』に代表される極太な網羅本よりもずっとずっとスリムにまとまっています。
また、解答も端的ながら十分な説明がなされており、効率よく典型問題を習得していくことができます。
まずはこの『基礎問題精講』で、典型問題・よくある処理を学んでいきましょう!
やり方としては、問題を見て、まずはすぐ手が動くかどうかを確認します。
解説されずとも今自分が持っている力で解ける問題もあるはずです。それはそれでよいので、自力で答えを出すところまでやりましょう。
最終的な答えが合っていれば、あとは解説を一読し、自分のこれまでの解釈通りだったかどうかを確認するだけでよいでしょう。
間違っていれば、そもそも方針・やり方はあっていたのか、単なる計算ミスなのか、誤りの原因をハッキリさせましょう。
3分程度考えてみて、手が動かない・糸口が見いだせないのであれば、すぐに解説を読みましょう。そして解き方を学びましょう。
無理に解法を覚えるというよりは、「なるほど、こうやったら確かに答えが出せるな」などと言った、少しばかりの感動を覚えながら理解を進めていきましょう。
納得出来たら、また自分でゼロから解き直します。解答の最初の1行が書けるかが大事です。ちゃんと答えまで出せればOK、ダメだったら再度確認、という流れで進めていきましょう。
その日やると決めた範囲の問題すべて一人で答えが出せるようになればクリアです。
そして、再度時間をおいて周回しましょう。
特に、1回目に初見で解けなかった問題については要注意です。2周3周程度回していって、もうこの問題集の中のどの問題についても正解できる!という状態になれば基礎は完了です。
(基礎なので、本当にそのレベルでないとだめです。応用問題の中では問題のわずかな1パーツとして出てくるようなところですから。瞬時に解き方が浮かび、すらすらと解答まで達しないといけません)
ⅠAとⅡBについては、それぞれこの本がしっかり身についたと思ったら、ぜひ共通テスト型の問題にも取り組んでみましょう。
これまでの共通テストやセンター試験の過去問、または各予備校が出している予想問題集でも構いません。
それぞれ時間を測って取り組んでみましょう。
特にセンター試験の過去問は練られた良問が多く、『基礎問題精講』で学んだことがどれだけアウトプットできるかを試すのに良い練習素材になっています。
当然、しっかり手を動かして解くことで、計算力も増します。
京都教育大学に合格するためには1次試験である共通テストでも高い点数が必要なわけですから、このタイミングでみっちり練習しておきましょう。
時期にもよりますが、1週間で2セットずつくらいのペースで進めると良いです。
毎日解きまくるのも良いですが、当然他の科目も勉強しないといけませんし、時間を置いてもう一度解けるかどうかを試す機会も必要です。しっかりと時間をかけて取り組みましょう。
解けなかった問題については、自分にとって何が足りなかったか(単に計算を間違えただけなのか、そもそも知らない解放だったのか、あるいは知っている解放だったけど引っ張ってこれなかったのか、など)を分析し、次に問題を解く機会に活かしていきましょう。
その過程でどんどん力がついていきます。
1週間に2セットであれば、1ヶ月もすれば8セットから10セット分くらいは問題が解けていることになります。
数をこなしているうちに雑になることなく、むしろ毎回それまでの学びを活かしながら有意義に解けているようであれば上出来です。
各セット完璧な状態にして、次のステップに進みましょう。
JR奈良校では自学自習の徹底管理・サポートを行い、
早稲田、関関同立、旧帝大、医学部医学科など数々の合格者を輩出しています!
詳細はこちらをご覧ください↓
3科目偏差値39から半年で立命館大学文学部(偏差値57.5)合格!偏差値18.5UP
英語偏差値40から半年で東京理科大学理工学部(偏差値60.0)に合格!
2ヶ月で模試総合点71点アップ!大阪大学工学部(偏差値62.5)に合格!
・2ヶ月で模試5教科660点→731点!大阪大学工学部に合格!
ホームページからのお問合せ・受験相談をお申し込みの方は、
こちらから申し込みください↓
国公立型の問題に挑戦!記述力を磨く!
・『基礎問題精講』シリーズが完璧(どの問題が聞かれてもしっかり自分で答えが出せる)になった
・共通テスト型の問題も8回分以上やり、見直しを重ねた結果どの問題についても解けるようになった
ようになったのであれば、もう土台としてはかなり盤石です。
次いで、京都教育大学の入試問題に向けて、国公立型の記述問題対策を進めていきましょう。
そのときにおすすめの問題集は、次の『CanPass数学』シリーズです。
『CanPass』は、数学のそれぞれの単元において学習効果の高い過去問を収録し、取り組む人の記述力を効率よく高めていくことを目的にした問題集です。
各問題について、詰まったときに良い切り口となる「思考のひもとき」がついています。
問題文の情報からどう解法知識を引き出していくか・何を試行錯誤していくかについての指南が載せられています。
これを見ると、その問題を自力で進めることができる可能性が増すほか、類似の問題や全くの初見の問題が出てきたときにも、どうアプローチしていけば良いか判断できる力が育ちます。
また、「解答」と「解説」が分かれており、実際の記述式答案では「解答」レベルの内容を書ければよいということがよく分かります。(問題集によれば、解答と解説が混合しており、実際にどこまで答案に書けばよいのか分かりにくいものもあります)
ⅠA・ⅡBについて約120問、Ⅲについて60問とそれなりの分量がありますが、「1日3つずつ進める!」などと数で目標を決めておき、それをコツコツと進めていくのが大事です。
『基礎問題精講』シリーズ同様、じっくり腰を据えて取り組みましょう。
すべての問題について、重要な考え方・キーポイントを誦じることができ、解答が再現できるようになれば合格です。
満を持して過去問演習に臨みましょう!
【JR奈良校で勉強し、当初思い描いていた以上の大学へ合格した生徒の例はこちら!】
【立命館】9月3教科偏差値39からの逆転合格劇 奈良育英高校再受験生
偏差値40から半年で東京理科大へ逆転合格!その勉強法の秘密とは?
過去問演習で得点力を伸ばす!
『CanPass』シリーズをやり込んだら、過去問に取り組んでみましょう。

120分ちゃんと時間を測って取り組むことが重要です。
これまでの学習経験からすぐに片がつく問題もある一方で、手強い問題にも遭遇するはずです。
特に、出題傾向のところでも述べた、教育大特有の「そもそも」問題については大きな壁となります。
最初は時間切れで解答を写すことになることも多いと思います。
しかし、証明例をいくつか書いているうちに、難しさの正体やカンドコロに気づいてきます。
「こういう風に書けばいいんだ!」や「ここまでなら書けそう!」というのが見えてくるはずです。
回を重ねるごとに成長していきたいものです。
また、作成した答案は、ぜひ指導できる人に見てもらって添削を受けると良いです。
数学の記述問題は「自分が解ける」だけではなく、採点官に伝わるような記述になっていないといけません。
教育大学の2次試験では特に重要視されるポイントです。
ぜひ、普段から個別指導してくれているような講師の方に見てもらうことをお勧めします。
このように演習を重ねていくうちに、過去問のストックがなくなってきたら、類似の出題が見られる他の教育大学の問題に取り組んでみるのも良いでしょう。
数学の「そもそも」問題については、北海道教育大学の問題や、奈良教育大学の問題がよく似ています。
「似た問題をもう少し解きたいな」となったときにはぜひチャレンジしてみると良いでしょう。
なお、奈良教育大学の数学については、こちらの記事もご覧ください。
京都教育大学の対策に通ずる部分も多いです。
【過去問分析】奈良教育大学に合格するために!数学の傾向と対策【参考書・勉強法】
【産近甲龍レベルを突破して、当初思い描いていた以上の大学へ合格した生徒の例はこちら!】
【立命館】9月3教科偏差値39からの逆転合格劇 奈良育英高校再受験生
偏差値40から半年で東京理科大へ逆転合格!その勉強法の秘密とは?
JR奈良校では自学自習の徹底管理・サポートを行い、
早稲田、関関同立、旧帝大、医学部医学科など数々の合格者を輩出しています!
詳細はこちらをご覧ください↓
3科目偏差値39から半年で立命館大学文学部(偏差値57.5)合格!偏差値18.5UP
英語偏差値40から半年で東京理科大学理工学部(偏差値60.0)に合格!
2ヶ月で模試総合点71点アップ!大阪大学工学部(偏差値62.5)に合格!
・2ヶ月で模試5教科660点→731点!大阪大学工学部に合格!
ホームページからのお問合せ・受験相談をお申し込みの方は、
こちらから申し込みください↓
















