こんにちは!
武田塾伊勢崎校です!
早速ですが今回は紙を折り重ねて月に行ってみたいと思います!!
え?
いやいや、そんなの無理だろうって???
まぁまぁ、落ち着いてくださいな、確かに紙を折って月まで行くのは物理的に不可能です。
ですので今回は、、、
何回紙を折り曲げたら、月の高さまで届くのか?
をテーマにやっていきたいと思いますっっっ!!
結論から申し上げますと、紙を42回、半分に折り重ねると月に届きます。
このお話ですが、高校生の時に聞いたとき実際に計算をしてみたことがあります。
あらかじめネタばらしをしますと、数学Bの数列範囲から「等比数列」の考え方を使います!
紙を半分ずつに折るとどうなっていくのでしょうか?
さて、今回は計算しやすいよう、折っていく紙の厚さを0.1mmとします。
ちなみに0.1mmというのは一万円札ほどの厚さです。
0.1mmの紙を1回折ると0.2mm、2回折ると0.4mmと折るごとに厚さは2倍になっていきます。
ということで、第ゼロ項を0.1、第一項を0.2、第二項を0.4、......としますと、
この数列の第一項を初項とすると、初項0.2、公比が2の等比数列ということになります。
この数列の漸化式は、
a(n+1)=2a(n)
となります。したがって、数列の一般項a(n)は
a(n)=0.2×2^(n-1)
です。n回紙を折り曲げると、a(n)[mm]の高さになるということがわかりました。
この紙を折り曲げた時の高さ(厚み)をhとしますと、
h=0.2×2^(n-1)・・・①
さて今回は結論を前述していますので、n=42 の時に、hは月の高さになるわけです。
実際に確かめ算をしてみましょう。
nasaのHPを参照しますと、
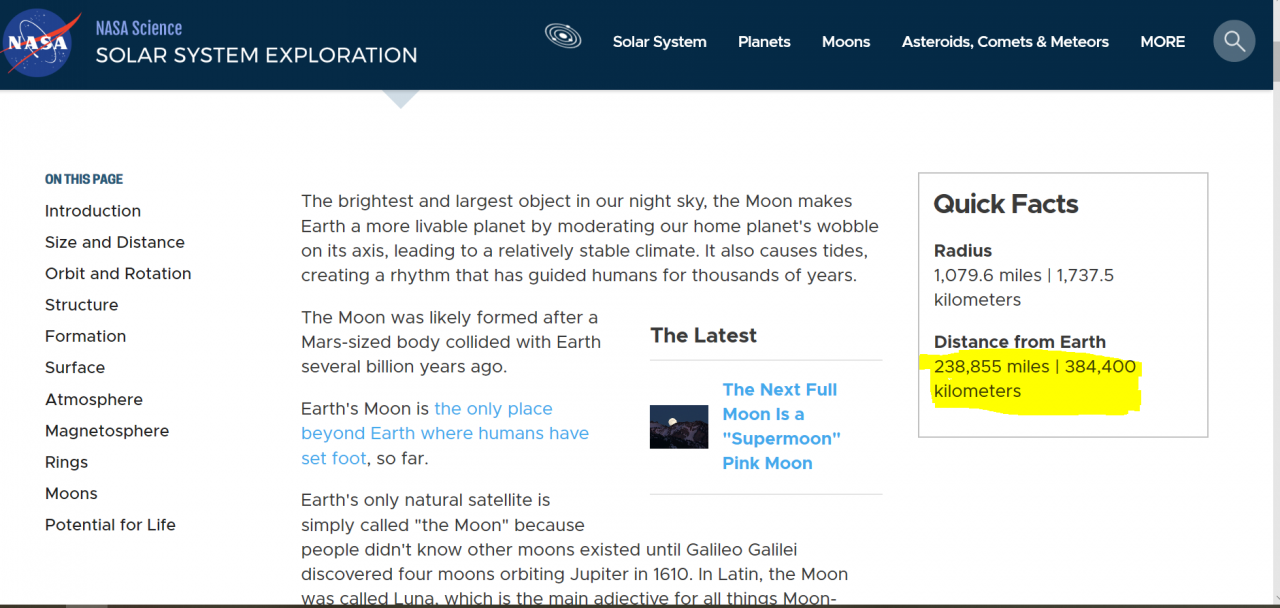
384.400kmだそうです!
384.400km=3.844×10^11mmなので、①の式に代入して、
3.844×10^11=0.2×2(n-1)
nについて解くと、(やむを得ず、計算ソフトを使用しました。)
0.2×2^(n-1)=3.844×10^11
2^(n-1)=1.922×10^12
n-1=log(1.922×10^12)/log(2)
n≒41.8057
ということでnの値はおよその42という確かめが出来ました。
残念ながら、、、
いやぁ、難しい計算でしたね、、、
机の上での答えは出ましたが、実際はそう簡単にはいきません。
紙を半分に折り重ねるとき、だいたい6回ぐらいでそれ以上折れなくなってしまいます。。
吹けば飛んでしまう、薄っぺらい紙でも折り重ねると月まで届くというのはなんだか不思議な話ですよね!
他の建造物でも計算してみてください!
今回使用した①の式と建造物の高さがわかれば、何回紙を折り重ねれば届くのか、計算することが出来ます!
学校の授業で習う数学にどんな使用方法があるか疑問に思うことがあると思います。
上記の計算はその一つの例で、他にも様々な使い道があります。
一緒に勉強頑張りましょう!!
武田塾では一人ひとり個性に合わせた勉強法や学習計画を一緒に模索しています!
勉強方法で悩んでいる方、自分一人ではうまく予定が立てられない方、一度武田塾に相談してみてはいかがですか?