満点以外あり得ない！「２次関数」徹底攻略マニュアル！　～初級編～

皆さん、こんにちは。

武田塾防府校です。

 

今回は数学Ⅰで習う「２次関数」を徹底解説していきたいと思います！

「２次関数」は共通テスト数学Ⅰ・Aでは確実に得点を稼ぎたい分野ですし、

根本の考え方は高校数学で一生使っていくことになります。

受験生のみならず、高１・２生の皆さんも早いうちに

２次関数をマスターすべく、是非読んでいってください！

"関数"とは。

２次関数の理解をスムーズに行うために、

「そもそも"関数"とは何なのか。」

について簡単にお話していきたいと思います。

ここの理解が"何となくになっている"か、

"しっかり出来ている"かの差は大きいです。

"yはxの関数"？

<"関数"とは>

2つの変数（色々な値をとって変わる数量を表す文字）x,yがあり、

xの値が決まればそれに伴いyの値がただ1つに決まるとき、

"yはxの関数である"と言う。

例えば

y=x²+x-2　という関数については、

"x=1のときy=0"となって

xの値を1つ定めるとyの値も1つ定まりますよね。

こんな関係性にあるxとyについての式で、

特に「y="次数が2のxについての多項式"」となっているものを

2次関数と言っているわけです。

 

また、関数を

f(x)=x²+x-2

のようにf(x)を使って表現をすることもありますよね。

これは単純に、「そう書くと色々と楽だから」という所が大きいです。

一度f(x)とおいてしまえばそれ以降は

x²+x-2 などの長い多項式を度々書かなくて済みますし、

"x=1の時、y=1+1-2=0"と書くよりも

"f(1)=1+1-2=0"と表記した方が簡潔で分かりやすいですよね。

微分・積分などのもう少し先の分野に入った時にも

こちらの表記の方が何かと便利だったりします。

 

余談ですが、f(x)のfは"function(関数)"の"f"です。

2次関数の基本

では実際に数Ⅰで習う2次関数と

それに関連する知識について見ていきましょう。

2次方程式とグラフ

皆さんは先に"2次方程式"と呼ばれるものを習ってきたと思います。

例えば

"x²+x-2=0はxについての2次方程式"

でしたよね。

2次方程式を解こうと思ったら基本的には、

①因数分解しようとしてみる

②ダメそうだったら解の公式を使う

と言う手順を踏むようにしましょう。

因数分解で解けるならそのほうが楽だからです。

こういった計算の簡略化、およびそのノウハウを積み重ねていくことは

ミスを減らしていく上でとても大事ですので、

数学では常に"楽が出来る方法"を探すよう心掛けましょう！

 

話がそれましたが、先程の2次方程式を解いていきます。

x²+x-2=0を因数分解すると

(x+2)(x-1)=0となり、

x=-2,1が求まります。

ここでやったことはxy平面上で考えるならば、

"y=x²+x-2というグラフ"と"直線y=0(x軸)"の交点

を求める作業と同じことです。

 

直線y=x+2と直線y=2x+3の交点を求める時に

x+2=2x+3を解いてそのx座標を求めるように、

放物線y=x²+x-2と直線y=0(x軸)の交点を求めるために

x²+x-2=0を解いてx座標を求めているのです。

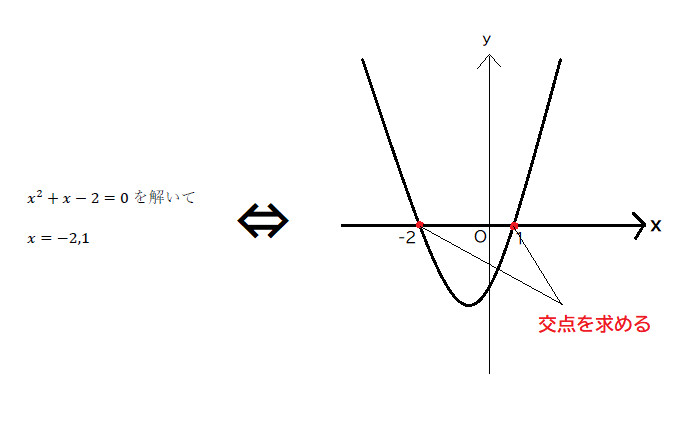
2次関数分野ではこのように、

"2次方程式f(x)=0を解くこと"と"y=f(x)のグラフの概形をイメージすること"

をリンクさせて解釈することが重要です。

判別式Dとグラフ

少し話を進めて、判別式Dと2次関数の関係性を見ていきます。

そもそも判別式Dって何者だったか覚えていますでしょうか？

機械的に判別式を使っていたという方は

ここでしっかり覚え直しておきましょう！

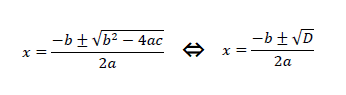
こちらは2次方程式ax²+bx+c=0(a≠0)の解の公式です。

この公式の中に現れるルートの中身、

"b²-4ac"の部分を判別式Dとおいていたんでしたね。

 

なのでax²+bx+c=0(a≠0)の解について

ルートの中身が正の値ならばそれは実数として成立し、√Dは＋と－に、解は2つに分岐する
→D>0のとき、異なる2解をもつ

ルートの中身が0ならば＋√D=－√D＝0となり、解が分岐しない
→D=0のとき、重解をもつ

ルートの中身が負ならば、それは実数ではない
→D<0のとき、(実数)解をもたない

ということが言えるのでした。

 

今回もそれぞれの状況で、

y=ax²+bx+c(a>0)のグラフの概形をイメージしておきましょう。

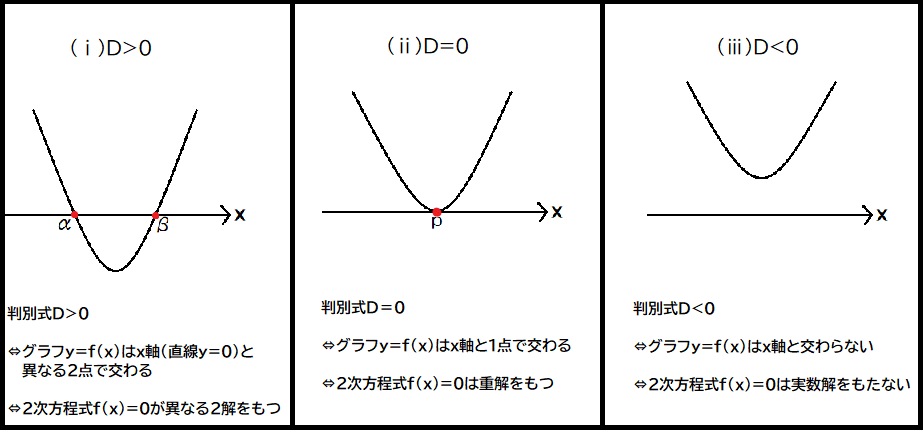
判別式がこうであるということは、

2次方程式の解がこうなっていて、

それはつまりグラフで表すとこうだ。

 

この辺りの変換をスムーズに出来るようになるのが

2次関数マスターへの近道です！

2次不等式とグラフ

x²+x-2<0
⇔(x+2)(x-1)<0…①
⇔-2<x<1…②

x²+x-2>0
⇔(x+2)(x-1)>0…③
⇔x<-2,1<x…④

いわゆるオーソドックスな2次不等式の解き方です。

 

皆さんは①→②、もしくは③→④の処理の過程で

何が起きているのかをグラフ的にイメージできますか？

もちろんイメージ云々の前に条件反射で解けるとしたら、

それは練度の現れでもあるので良いことです。

ただ、例に挙げたような基礎的な問題だけではなく、

応用問題にも対応していくためには

「何でそうなるのか。」まで押さえておくことが重要です！

この機会にグラフを見て、仕組みを確認しておきましょう。

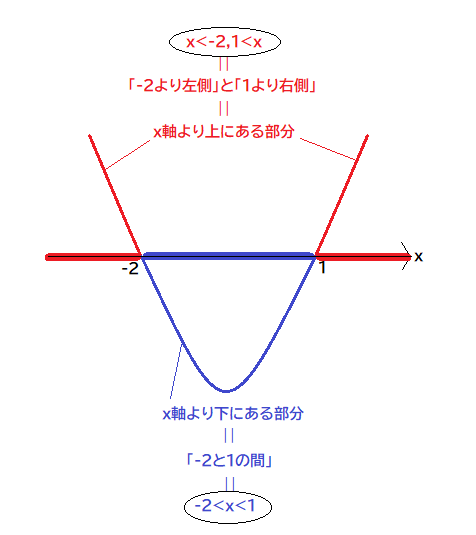
①式：(x+2)(x-1)<0　が表すのは、上図で示したように

「"(-2,0),(1,0)を通る下に凸の放物線"がx軸より下側にあるようなxの範囲」です。

同様に　③式：(x+2)(x-1)>0　が表すのは、

「"(-2,0),(1,0)を通る下に凸の放物線"がx軸より上側にあるようなxの範囲」です。

 

もしこの視点が欠けていた場合は、しっかり押さえておきましょう！

まとめ

今回は「２次関数徹底攻略マニュアル初級編」ということで、

２次関数の基礎の部分を解説していきました。

これら３つのポイントとグラフの概形の関連付け

は２次関数マスターには欠かせません！

しっかりと図形的にイメージし、根本から理解しておきましょう！

 

今後「２次関数の最大・最小」や「絶対値符号のついた２次関数」

などにも触れていこうと思いますので、続編をお待ちください！

無料受験相談実施中！

武田塾防府校では無料受験相談を

実施しています！

防府市近辺で塾・予備校をお探しの方、

受験に関して分からないことや不安がある方、

是非下記フォームよりお問い合わせください！

 

受験相談では現状の分析をした後に、

”いつまでに何をどういう風にやれば良いか”

詳しくお教えいたします！

 

皆様からのご応募、心よりお待ちしております！

武田塾防府校の自習室・休憩スペース

自習室

自習室は落ち着いた静かな空間になっており、

机には仕切りもついているので、

集中して勉強できること間違いなしです！

 

【自習室利用可能時間】

曜日	自習室利用可能時間
月	13:00~22:00
火	13:00~22:00
水	休館日
木	13:00~22:00
金	13:00~22:00
土	13:00~22:00
日	13:00~19:00

リフレッシュスペース

武田塾防府校には

塾らしからぬオシャレな

リフレッシュスペースがあり、

勉強に疲れたらここで休憩

できるようになっています！

（飲食も可能！）

お茶やコーヒー、りんごジュース等が出せる

ドリンクサーバーも自由に使えます！

防府校SNSアカウント

武田塾防府校の

LINEアカウント

を開設いたしました！

こちらからのご相談も受け付けておりますので、

友だち登録よろしくお願いします！

 ↓↓↓↓↓

防府校LINE

 

武田塾防府校へのアクセス

〒747-0034
山口県防府市天神1-10-14

JR防府駅から徒歩7分
（旧国道2号線沿い、アルク防府店の隣）

武田塾防府校の
ホームページTOPは＜コチラ＞

武田塾は”山口市”にも！

武田塾は山口市にもあります！

こちら武田塾山口校の自習室の様子です。

生徒たちはいつでも集中モード！

 

武田塾山口校のHPは＜コチラ＞

武田塾に興味があって

山口市近辺にお住まいの方は

是非チェックしてみてください！