【学校では習わない】「数学嫌い」な人必見！誰でも「数学好き」になる話。

皆さん、こんにちは！

武田塾防府校の中村です！

 

今回は『数学の見方』に関するお話です。

「数学が嫌い、苦手！」という方こそ色んな発見があると思いますので、是非読んでいってください！

数学の”面白さ”を見出そう！

”数学”って本当に好き嫌いの分かれる科目です。

国語、英語、英語、社会、理科の５教科の中だと、

好きな人が一番多いのも、嫌いな人が一番多いのもどっちも”数学”なんだとか。

それでいて、受験において数学はとても重要な科目、

というのもまた事実なんですよね。

 

中には数学が嫌だからと言う理由で文系を選んだり、

受験で数学が必要無い大学・学部を探したりしている方も

いるのではないでしょうか？

そう考えると数学のせいで選択肢の幅を狭めてしまっているようで

なんだかもったいないですよね。

 

もちろん科目の好き嫌い、得意不得意は人それぞれなので、

「数学を好きになれ！」と言うつもりは毛頭ありません。

が、今数学が嫌いな人の中には

「数学を面白いと思う"きっかけ"が無かった」

だけの人もいると思うんです。

この記事が、そんな方の"きっかけ"の１つになれば幸いです。

数学のあれこれ

①無限等比級数（？）

1+1/2+1/4+1/8+・・・の値を求めよ。

この問題、皆さんはどう考えますでしょうか？

無限等比級数の考え方を学んだ方なら、

「初項」を「1と公比の差(1/2)」で割って、答えは「2」

とすぐに解けるかもしれません。

 

ですが実はこれ、図形的に考えてみると誰でも答えが想像できます。

こちらの画像をご覧ください。

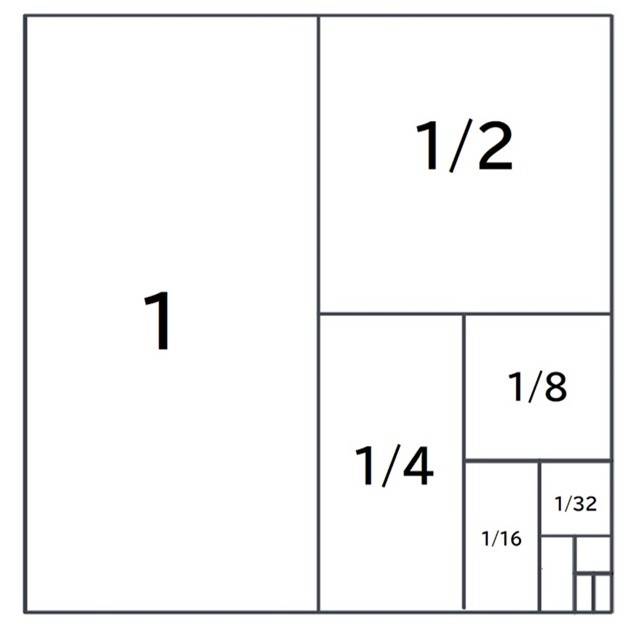
1+1/2+1/4+1/8+・・・

の最初の「１」は図の四角形の左半分の面積です。

2番目に出てきた「1/2」は四角形の右上部分の面積です。

同じように、1/4、1/8、1/16・・・と無限に足していくと

「面積２」の四角形にどんどん近づいていくことが分かるかと思います。

実際、最初に出した答え「２」と一致しますね。

 

数列だ極限だ無限等比級数だなんだと言われると

堅苦しく聞こえるかもしれませんが、

こう見てみるとやっていることは簡単ですよね！

②Ants問題

次はちょっと数学から近からず遠からずのお話になります。

 

Ants問題とは"Ants"、つまり"アリ"に関する問題です。

簡単のために少し内容を改変しますが、以下のような問題になります。

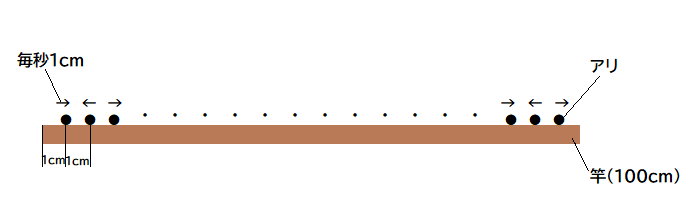
例えば左から数えて1番目のアリは、

2番目のアリと0.5秒後に竿の左端から1.5cmの地点で衝突し、

その後左を向いてさらに1.5秒歩いて竿から落ちます。

この場合、1番目のアリは歩き始めて2秒後に落ちたことになりますね。

じゃあその事象が99匹のアリ全てに起こると考えて、

最後のアリが落ちるのは何秒後でしょう。

というような問題です。

 

1番目のアリについては1回目の衝突で済みましたが、

10番目や20番目、あるいはおそらく一番最後まで残るであろう

真ん中付近のアリについては

結構な回数の衝突を繰り返しそうですよね。

結果的に落ちるまで何秒かかるのか、

順当に考えて導出するのはかなり骨が折れそうです。

 

ですが実はこれ、少し視点を変えると一瞬で答えが出るんです。

「最後に落ちるのは"どの"アリか」は聞かれていないのも1つのポイントです。

 

アリ同士はぶつかると向きを変えてまた歩き出す、という設定でした。

しかしアリ1匹1匹の区別が必要無い今、どのアリもお互いにすり抜け、

ただただ直進し続けていると考えても大丈夫なのです！

どういうことか、下の図を見るとイメージしやすいかもしれません。

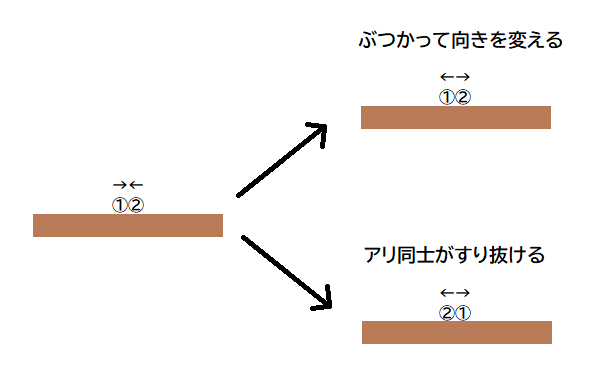
アリ①とアリ②がぶつかって向きを変えた場合と

お互いにすり抜けた場合で違ってくるのは

アリ①とアリ②の位置関係のみです。

アリに区別が無ければまったく同じ状態です。

 

これが全アリについて起こると考えると、

竿から落ちるまでに一番時間がかかるのは

最初に一番左にいた、竿の右端を目指して歩くアリですよね。

よって、答えは99秒です。

実際に99秒後に落ちるのは別のアリですが、

秒数を求めるだけならこれでOKなんですね！

 

まとめ

少し例が極端だったかもしれませんが、

数学にはこのように、視点を変えると処理が楽になるシーンが多くあります。

例えば確率の問題で事象Aが起きる確率を考える時に、場合によっては

Aの余事象が起きる確率を考えた方が早かったりしますよね。

 

この「視点を変える」という所に数学力が要求されているような気がして、

難しさを覚えてしまっている人もいるかもしれません。

ですが、いつもアドリブで視点を変えているわけではないのです。

英語で英単語、古文で古文単語を暗記するように、

高校数学も結局は、

色んな問題に触れる中で「問題パターンや視点の変え方を暗記」することが大事なんです。

見た目上の難解さで数学から距離を置いてしまっている人は

数学も他科目と同じように少し頑張って勉強してみて、

数学も要はパターンなんだ、と思える状態を目指しましょう！

 

数学を味方につけると、

また視野・選択肢が広がるかもしれませんよ！

無料受験相談実施中！

武田塾防府校では無料受験相談を

実施しています！

防府市近辺で塾・予備校をお探しの方、

受験に関して分からないことや不安がある方、

是非下記フォームよりお問い合わせください！

 

受験相談では現状の分析をした後に、

”いつまでに何をどういう風にやれば良いか”

詳しくお教えいたします！

 

皆様からのご応募、心よりお待ちしております！

武田塾防府校の自習室・休憩スペース

自習室

自習室は落ち着いた静かな空間になっており、

机には仕切りもついているので、

集中して勉強できること間違いなしです！

 

【自習室利用可能時間】

曜日	自習室利用可能時間
月	13:00~22:00
火	13:00~22:00
水	休館日
木	13:00~22:00
金	13:00~22:00
土	13:00~22:00
日	13:00~19:00

リフレッシュスペース

武田塾防府校には

塾らしからぬオシャレな

リフレッシュスペースがあり、

勉強に疲れたらここで休憩

できるようになっています！

（飲食も可能！）

お茶やコーヒー、りんごジュース等が出せる

ドリンクサーバーも自由に使えます！

防府校SNSアカウント

武田塾防府校の

LINEアカウント

を開設いたしました！

こちらからのご相談も受け付けておりますので、

友だち登録よろしくお願いします！

 ↓↓↓↓↓

防府校LINE

 

武田塾防府校へのアクセス

〒747-0034
山口県防府市天神1-10-14

JR防府駅から徒歩7分
（旧国道2号線沿い、アルク防府店の隣）

武田塾防府校の
ホームページTOPは＜コチラ＞

武田塾は”山口市”にも！

武田塾は山口市にもあります！

こちら武田塾山口校の自習室の様子です。

生徒たちはいつでも集中モード！

 

武田塾山口校のHPは＜コチラ＞

武田塾に興味があって

山口市近辺にお住まいの方は

是非チェックしてみてください！