【検証】中央大の数学、武田塾の参考書で解ける説！？武田塾拝島校

中央大検証数学

こんにちは！
拝島駅から徒歩3分！逆転合格でおなじみ、武田塾拝島校です！

受験勉強、飽きずに頑張っていますか？偉いです！

「このまま参考書で続けていれば、本当に入試に直結するのかなぁ？」と気になっている方、お立ち寄りください。

「武田塾の参考書ルート検証企画」！！！

今回は第３弾(後編) 中央大学数学・化学です。前編の英語はこちら。

入試問題と参考書を照らし合わせて、実際にどのくらい役に立つのか、検証してみました！

基礎問題精講、リードLightノートなどをマスターしていれば解ける問題が続々！！

☆シリーズバックナンバー☆

【検証】東工大入試、武田塾の参考書で解ける説！？武田塾拝島校

【検証】一橋大入試、武田塾の参考書で解ける説！？武田塾拝島校

～私たち武田塾は生徒一人ひとりの自学自習の充実に向け、勉強法やペース作りをサポートしています。

そこで、何より一番知っておいていただきたいのが参考書を完璧にすることの重要性です～

武田塾の参考書で入試問題にどこまで太刀打ちできるようになるのか。一緒に確認しましょう！

今回は、中央大学の2022の入試問題で検証していきます！

中央大学理工学部数学

1. 数学 2022 大問1

中央大学理工数学2022の大問１は「定積分で表された関数」に関する問題でした．

中央数学大問１

定積分で表された関数を求める問題では，「定積分は定数になっている」ことに着目することがポイントです．

今回の中央大の問題では誘導がついていますが，このポイントが分かっていれば，問題の全体像を瞬時に把握することができ，誘導にも乗りやすかったでしょう．

この問題の類題は『数学Ⅲ基礎問題精講』の例題100番や『数学ⅡB 入門問題精講』の第６章の練習19番にあります．

（基礎問題精講や入門問題精講の問題は，定数となる定積分が１つしかないので，一次方程式を解くことになりますが，今回の中央の問題では定数となる定積分が２つあるため，連立方程式を解くことになります．）

またこの中央大学の問題では，(ウ)~(オ）の空欄を埋める際に三角関数の積分を計算する必要があります．

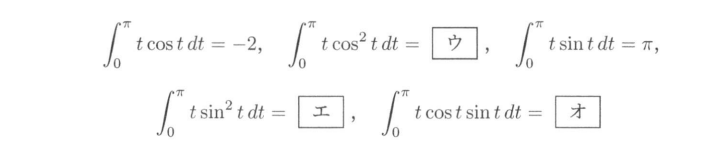
中央数学大問１積分の計算

この積分は，「三角関数の二次式（sinθの２乗，cosθの2乗やsinθcosθなど）は，「半角の公式」を用いて次数を下げてから積分する」というポイントを押さえていれば，容易に計算することが可能です．

このポイントは『数学Ⅲ入門問題精講』の練習問題４で解説されています．

中央大の問題は次数下げを行うことで，t sin2tおよびt cos2tの積分に帰着することができます．

この形の積分のやり方は『数Ⅲ入門問題精講』の第6章練習問題12において解説されています．この問題でxsinxの積分をできるようになっていれば，今回の中央大の積分も簡単にできたでしょう．

中央大理工数学×基礎問題精講

1. 数学 2022 大問３

中央大理工数学2022の大問３は数Ⅲの微分積分に関する設問でした．

中央理工大問3

(2)では，y=f(x)の変曲点を求める必要があります．

変曲点に関する問題は，『数学Ⅲ基礎問題精講』の例題71番にあります．

今回の中央大の問題のf(x)と基礎問の問題では，符号が違うだけで関数の形は同じです．

そのため全く同じように解き進めることで変曲点を求めることができたでしょう．（変曲点のy座標の符号が異なるだけです．）

中央大理工数学×基礎問題精講

1. 数学 2022 大問４

中央大理工学部2022の大問４(1)は３次方程式の因数分解および解の判別に関する問題でした．

中央大問４

この問題のように３次式を因数分解する場合は，因数定理を用いて１次の項の因数を見つけます．

その上で，3次方程式の解の判別を行う際は，因数分解した時の2次式の判別式を考えます．

この問題とほぼ同じ問題が『数学ⅡB基礎問題精講』の例題30にあります．この問題で，3次式の因数分解および３次方程式の解の判別の流れをつかめていれば，今年の中央大の問題も容易に解答できたでしょう．

中央大経済数学×入門問題精講＆基礎問題精講

1. 数学 2022 大問1

中央大学経済学部2022の大問１は，様々な分野の基礎的な問題が並ぶ小問集合でした．

中央大学経済数学1

(1)は３進法に関する問題です．『数学ⅠA基礎問題』の例題91がその類題です．

(2)は条件付確率に関する問題です．『数学ⅠA基礎問題』の例題129がその類題です．

(3)は三角関数の不等式に関する問題です．

cosθの２乗をsinθの２乗に直してから不等式を解きます．

『数学ⅡB入門問題精講』の練習問題8や『基礎問題精講』の例題74が類題になります．

(4)は対数関数を用いて累乗の桁数を求める問題です．

『入門問題精講』の練習問題18や『基礎問題精講』の例題75がその類題になります．

(5)は３次関数の接線の方程式を求めたら，あとは連立方程式を解くだけです．

『数学ⅡB入門問題精講』の練習問題５がその類題です．

(6)は二次関数と直線で挟まれた部分の面積を積分により求める問題です．

『数学ⅡB基礎問題精講』の練習問題16や『基礎問題精講』の例題105が類題になります．

中央大理工化学×リードLightノート化学

1. 化学 2022 大問1(3)

中央2022化学の大問1の(3)は反応速度および活性化エネルギーに関する問題でした．

中央化学1-3

反応速度や活性化エネルギーに関する問題は『リードLightノート化学』に多数掲載されています．(第７章基礎CHECKなど)

これらの問題を解いていれば，

「温度を高くすればすると，活性化エネルギー以上のエネルギーを持った分子が増加するために，反応速度が上がること」

が分かるため，(イ)は誤りであることが分かります．

また，『リードLightノート化学』の126番において，

１　エネルギー図において活性化エネルギーはどこの部分を意味するか？

２　エネルギー図において生成熱はどこの部分を意味するか？

を理解しておけば，(ウ)の「正反応と逆反応の活性化エネルギーによって生成熱が求められる」は正しいことが分かるでしょう．

中央大理工化学×リードLightノート化学

1. 化学 2022 大問1(4)

中央2022化学の大問1(4)も化学に関する基礎的な知識を問う問題でした．

中央化学1-4

(ア)はトタンの仕組みに関する問題です．

これは『リードLightノート』の例題191にあります．

この問題の解説では，トタンの仕組みをイオン化傾向を用いて詳しく説明されています．

武田塾の方針に乗っ取って，「なぜトタンにおいては亜鉛が先に参加されるのか？」を説明できるようにしておけばこの問題は解答することができたでしょう．

なおトタンについては『化学　重要問題集』の168番においても解説されています．この重要問題集の問題では，(ア)の問題文の内容(トタンの仕組み)を自力で記述させています．

そのため，この問題を解けるようになっていれば，中央大学の問題において選択肢を選び間違えることはなかったでしょう．

(イ）は溶解度積によって沈殿が生成するかが判定できることを問う問題でした．

『リードLightノート』の151番では，実際に[Ag+]と[CL-]の積とAgClの溶解度積を比べることで沈殿の生成を判定しています．

この問題を解いていれば，中央大の今年の入試問題も解けたでしょう．

（ウ）は蒸気圧降下に関する問題でした．これは全く同じ問題が『リードLightノート』の第４章の基礎チェックにあります．

中央大理工化学×リードLightノート化学

1. 化学 2022 大問1(7)

中央大化学2022の大問1(7)は鉛蓄電池に関する問題でした．

中央化学1-7

鉛蓄電池の負極/正極の質量の増加，および希硫酸の質量を求める問題は『リードLightノート化学』の117番にあります．『リードLightノート』の問題においては，初めに陽極に発生した気体の体積から放電した電子のmolを求める必要があります．一方，今回の中央大の問題では，すでに放電した電子のモルは与えられています．

中央大の問題のほうがリードLightノートの問題よりも簡単に求めることができるので，本番は落ち着いて解き進めることができたでしょう．