「数学の区分
数学にはⅠ・A・Ⅱ・B・Ⅲと区分けがなされています。
これらは、文部科学省の学習指導要領に基づく区分けであり、一般に高校1年でⅠ・A、2年でⅡ・B、3年でⅢを扱うことが多いかと思います。
では数学Ⅰ・Aが最も簡単で、数学Ⅲが最も難しいのかと言われると、見方によってはYES、違う見方によってはNOと答えることになるでしょう。
これらはそれぞれ異なる特徴を有しており、一概に「難しいのは〇〇」と言う事自体が難しいのです。
今回は数学Ⅰ・A・Ⅱ・B・Ⅲそれぞれのキャラクターと、それを踏まえた対策をこれから述べていこうと思います。
(平成30年度に文部科学省によって2022年度から新学習指導要領へと変更するという告示がありました。
「ベクトル」が数学ⅠAⅡBから消えるという衝撃的な変更ですので、詳しくは文部科学省の新学習指導要領をご覧ください。
今回は2021年現在適用されている現行の学習指導要領に基づいて話していきたいと思います。)
数学Ⅰ・Ⅱ・Ⅲ vs 数学A・B
まずは大きな分類の特徴として、数学Ⅰ・Ⅱ・Ⅲと数学A・Bの違いから。
数学Ⅰ・Ⅱ・Ⅲは主に関数・グラフを扱えるようにする事を大きな目的としています。
この為、これらは関連しており、数学Ⅱを理解するには数学Ⅰの知識が、数学Ⅲを理解するには数学Ⅰ・Ⅱの知識が必要なので、積み上げていく事が重要となります。
しかし、問題のバリエーションは実はそこまで多くはなく、問題をパターン化していくパターン学習がかなり有効です。
つまり、問題集に載っている例題の解法暗記が得点力に比較的直結しやすい分野なのです。
一方数学A・Bは、整数、図形、場合の数・確率、数列、ベクトル、(加えて、必須ではありませんが確率分布)と分野毎に独立しています。
その為、(融合問題などを除き)1つの分野の内容をおさえれば、ある程度得点できるようになると思います。
最悪詰め込み学習でなんとかなってしまう分野かもしれません。
しかし、問題のバリエーションは数学Ⅰ・Ⅱ・Ⅲに比べると多く、問題の内容を基礎的な内容へと切り分ける能力や整理する能力が要求されます。
また、証明問題も数学Ⅰ・Ⅱ・Ⅲに比べ多く出題されるので、論理的に説明できる能力が試されます。
では次に個々のキャラクターについて述べていきます。
数学Ⅰ:数と式/図形と計量/二次関数/データの分析
中学でやった内容も多く含まれており、比較的とっつきやすいかもしれません。
しかし、これらはこれ以降の数学を理解する上で欠かすことのできない分野であり、中途半端な理解では後で苦しむことになります。
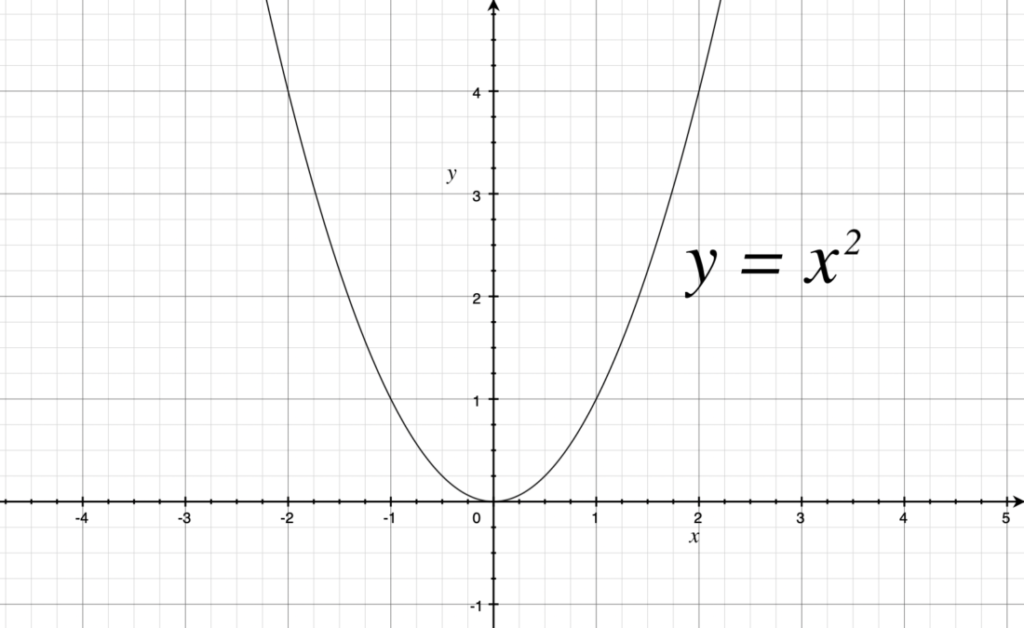
特に「二次関数」では、関数とは何なのか、グラフの移動、グラフの書き方、最大値・最小値の求め方など、今後の学習に活きるエッセンスが詰まっています。
少なくとも「二次関数」については、なぜこのような解答の書き方になるのか、なぜこのような方針をとるのかについてしっかりと理解して下さい。
時間はかかるかもしれませんが、それを怠って先へ進むとより時間がかかることになると思います。
数学Ⅱ:いろいろな式/図形と方程式/指数関数・対数関数/三角関数/微分・積分の考え
数学Ⅰとは比べ、覚えるべき定義や公式がかなり増えており、ここで数学嫌いになる人も多いかもしれません。
数学Ⅱを乗り切るには、定義や公式に慣れる事がとにかく重要です。
定義や公式の証明は大事なのですが、まずは基本的な問題を解いて公式を使えるようにしていきましょう。
また、問題のパターン学習は定義や公式が難しい分、数学Ⅰに比べより有効であるように感じます。
まずは問題が解けるようになる事を第一目標とし、その上で余裕があれば公式の証明についても勉強しましょう。
公式の導出方法について学ぶべき理由は、難関大学でたまに公式の証明自体が出題される事があるというのに加え、また公式の証明の考え方を基礎とした問題が出題される事が結構あるからです。
特に後者については、問題に対する見方が変わると思いますので、公式の導出方法について一度は体験しておくことをおすすめします。
ただ、繰り返しになりますが、まずは公式をきちんと用いられるようになる事が重要です。
それが出来るようになる前と後では公式の証明方法の理解度も変わってくると思います。
数学Ⅲ:平面上の曲線と複素数平面/極限/微分法/積分法
理系学部志望の方のみが学習する、いわばボーナスステージです。
今「ボーナスステージ」と言ったのは追加でやらねばならないという意味だけではなく、文字通り点が取りやすい「ボーナスステージ」だからです。
実際、数学Ⅲを勉強した殆どの方は、「数学Ⅲが一番簡単」と言います。
確かに、数学Ⅲの入口(定義や公式)は難しい感じを醸し出していますが、意外と出口(応用問題の難易度やひねり方)はそこまで高くありません。
東大でさえも、最近であれば2019年度に積分だけをさせる問題が出題されているぐらいです。
また、実は入り口も数学Ⅱの微分・積分と被る内容であり、新しい公式を使いミスなく計算ができるようになるだけでかなりの得点力をつけることが出来ます。
ただ、数学Ⅱ以上に定義や公式の理解を確認する問題が出題されますので、数学Ⅲでは定義や公式を含め基礎をきちんと押さえた学習を行えばより得点力UPに繋がるはずです。
ただ、くどいようですが、まずは公式を使えるようになる事、計算をミスなくこなせるようになる事が第一目標です。
数学を理由に理系をあきらめるのはナンセンス!
「理科が苦手だから」という理由ならまだしも、「数学が苦手だから」という理由だけで理系を志すのを諦めるというのは非常にナンセンスだと個人的に思います。
数学Ⅲは数学の分野の中でひねりが最も少ないですが、計算力によって意外と差がつく「ボーナスステージ」です。
数学が苦手な人こそ(取れる数学Ⅲの問題に時間を割けるという意味で)得点しやすい分野なのです。
それに、文系では実は数学で差がつくと言われています。
数学が試験科目にない学部でない限り、数学からの呪縛からは解き放たれません。
じゃあどうすればいいんだ!って話かもしれませんが、間違いなく言えることは「数学が苦手だから、文系に進む」というのは全くもって間違っているという事です。
できれば「歴史をもっと学びたいから」「本が好きだから」「将来文系の仕事に就きたい」などというポジティブな理由が理想です。
ネガティブな理由にしても「理科がもう生理的に無理」くらいの、理系に進んだときにどんなにデメリットがあるのかを考えられるといいかと思います。
数学A:場合の数と確率/整数の性質/図形の性質
これらはとっつきやすく入口は簡単に見える分、問題の難易度やひねり方、バリエーションはピンキリで、「どうやったらこの発想に至るんだ!」というものも少なくありません。
大事なのはやはり基礎の問題ではありますが、基礎の問題を解く上においても着眼点や方針について注意してください。
おそらく、入試で見る問題が問題集で解いた問題とほぼ一緒という事はほぼ無いでしょう。
その為、基礎のうちからなぜこのような発想に至るのか、なぜこのような解答の書き方になるのかをきちんと学ぶ事で、応用問題にも対応しやすくなると思います。
では数学Aのそれぞれの単元についてまとめていきます。
場合の数と確率
「このようなシチュエーションではこのような計算の仕方をする」
というパターン認識能力と、
「計算しやすいように漏れなく重複なく切り分ける」
場合分けの能力を共に要求されます。
パターンについては基本的な問題で学んでほしいのですが、場合分けについては応用問題を解きながら学んでいくほかありません。
ある程度基本が身についたと思えば、応用問題に手を付け、解答の場合分けと自分の場合分けを比較する事が大切です。
計算しにくさや、重複や漏れの出やすさが一つの指標ですが、とにかく自分で考えてみましょう。
自分の解き方がなぜダメなのかについて、自分で一旦考えたうえでどうしても分からなければ学校の先生や塾の講師に相談してみて下さい。
また、場合の数と確率は数列の漸化式と密接に関わっており、最初は理解が難しいかもしれませんが、出来るようになると得点源となります。
何からやればいいのか分からなければ、個人的には「場合の数と漸化式」「確率と漸化式」を解けるようになる事をおすすめします。
整数の性質
この単元で差がつくのは証明問題でしょう。
整数問題では、どこの参考書にも載っているような3つの有名な解法
①因数分解して積の形に
②余りで分類
③大小関係などで絞り込み
がありますので、まずはそれを意識して基本問題を解きましょう。
また、本当に難しく手も足も出ない問題も中には有りますので、とらわれすぎないというのも重要かもしれません。
図形の性質
大学入試ではこれ単独の問題はほとんど出題されていませんので、まずは他の単元(図形と計量、図形と方程式、ベクトルなど)で出て来た図形の性質についてその都度確認するくらいでいいのかもしれません。
ただし、方べきの定理だけは頭に叩き込んでおきましょう。
証明は難しいわけではないのですが、使えると便利ですのでぜひ覚えておいてください。
数学B:数列/ベクトル/確率分布と統計的な推測
これらは分野が独立しているので、いきなりそれぞれの単元について述べていきます。
数列
高校1・2年にとってΣ計算と漸化式と数学的帰納法はこの単元で初めて出てくる事項ですが、
「この3つが出来る=数列が得意」といっても過言ではないくらい重要事項です。
Σ計算は数列において欠かせないですし、漸化式は数列に限らず、場合の数と確率などの他分野にも関わってきますので、問題を解いて慣れていく事が大切です。
また、数学的帰納法は自然数nが関わる証明問題に対し猛威をふるいます。
また、漸化式の解法の最終手段として用いられる事もあるので、是非とも身に付けて頂きたい証明方法です。
ベクトル
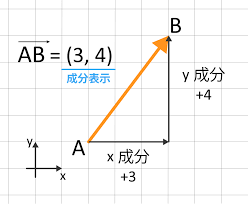
ベクトルという概念自体初めて出てきますので、最初は面食らうと思います。
しかし色々な解法パターンが生じやすい図形問題の解法で一番簡単に解ける解き方はベクトルなのではないかと思うぐらい、強力かつ万能なツールなので、問題を解きながら慣れていきましょう。
一番重要なのは、どんな問題であってもまず最初にやる事は何かという事です。
「始点をそろえる」
「一次独立なベクトルを(平面の場合)2つまたは(空間の場合)3つおく」
「ベクトルの絶対値と内積を求める」
などでしょうか。
これは基本問題から意識しておくと、複雑な問題をみてもあたふたせずに済むと思います。
確率分布と統計的な推測
あくまでも現在の学習指導要領での話になりますが、この単元は二次試験では(期待値以外は)まず出題されないでしょう。
その為、共通テストの選択問題でも殆どの人が選択しないと思います。
実は大学に入ってからは重要になるのですが、高校生の間での優先順位は限りなく低いと考えてもらって構いません。
以上、長々と書いてきましたが、今回伝えたかった事は3つあります。
・「理解して問題を解く」よりも「問題を解いて理解する」
・「入口」が険しい程、「出口」は険しくない
・「数学が苦手」≠「理系学部は無理」
ここまでお付き合い頂きありがとうございました。
香芝市五位堂駅周辺の大学受験個別指導学習塾・予備校ならE判定から逆転合格!授業をしない。武田塾五位堂校
勉強・受験に関して悩んでいる方、香芝市五位堂駅付近の予備校・個別指導学習塾選びに迷っている方、逆転合格を目指す方、お気軽に無料の受験相談へお越しください!
全て無料で相談をお受けしております!
何から勉強に手を付けてよいか分からない高校生
どの大学にすべきか分からない高校生
苦手教科の勉強方法を教えて欲しい高校生
大学受験受験教科毎の勉強の割合をどうするべきか分からない高校生
大学受験共通テストの勉強方法と時期はどうすべきか分からない高校生
そもそも単語が覚えられない高校生
大学受験すべきか分からない高校生
お金をかけずに大学に進学する方法を知りたい高校生
具体的な英検対策を知りたい高校生
1年で偏差値を11以上伸ばす方法を知りたい高校生や親御様は是非武田塾五位堂校にご相談にお越しください。
香芝市瓦口2153ノーブル壱番館1F
香芝市五位堂駅徒歩3分

















