【高1・高2向け】数学はスゴイ！文系にも知ってほしい数学の魅力

みなさん、こんにちは。

武田塾古市校です！

今回は、文系にも理系にも知ってほしい数学のスゴさについて、お話しようと思います。

「数学ニガテだし、文系に進むつもりだし、数学はなぁなぁでいいや」

と思っている方にも、数学って結構...スゴイじゃんって思ってくれたら幸いです。

job_suugakusya

高校数学では様々な数学の分野を学びますね。

代数、数列や、幾何学に始まり、確率と微積分にも触れるでしょう。

中学で学んだ数学から、かなりステップアップして、苦手意識を持ってしまう学生も多いです。

でも、数学のスゴさ、重要さを知らないままはもったいない！

理系はもちろん、文系の方にも数学は是非々々知っててほしいんです！

数学は世界共通の言語！
実生活に即した数学、確率・統計は世の中の見方が変わる！
1. 人の直感に反する確率
2. 稀な現象にも数学法則が働いている！
まとめ

数学は世界共通の言語！

かの有名なガリレオ・ガリレイの名言に、

“La matematica è l'alfabeto in cui Dio ha scritto l'universo”（数学は神が宇宙を書いた言語である）

というのがあるそうです。

実際、物理などの学問は数学という「言語」を使って、宇宙の法則を記述しようとしています。

例えば、アインシュタインが導いた、エネルギーと質量を結ぶ方程式、

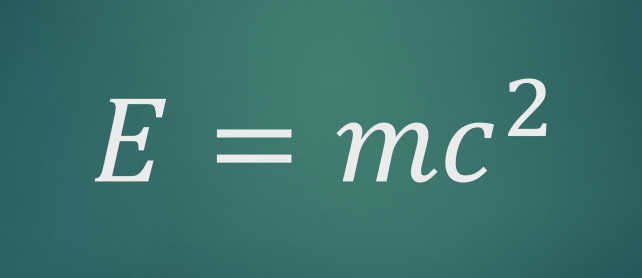
MicrosoftTeams-image

は世界一美しい方程式ともいわれ、シンプルながら、「宇宙の真理」に迫る方程式です。

この簡素な方程式は、いくつかの原理（証明の要らない基本法則）から出発して、

物理的な考察と数学的な手続きを経て導かれています。

エネルギーと質量が等価である、なんて突飛な話が言えるのは、

数学という言語を用いたから!日本語や英語では、言葉を尽くしてもできる芸当ではないのです。

物理をはじめとする様々な科学は数学という唯一無二の言語の力を存分に利用しているのです。

現代の発展した科学の礎は、数学のパワーによるとことが大きいのは、言うまでもないでしょう。

実生活に即した数学、確率・統計は世の中の見方が変わる！

数学は言語！なのはいいけど、やっぱり使わないよ、と思うかもしれません。

宇宙の法則を記述する言語として、すさまじい威力を発揮する数学ですが、

とはいえ、もっと実生活に即した魅力がなければ、どうにも興味が...。

わかりやすく、身の回りに存在している数学といえば、確率・統計でしょう。

偏差値や、天気予報や、病気の感染者数の予測など、

実生活に根付いた予測において、広く使われている数学です。

c2e85ce4ef8d6233ee1a94932ba585e9_t

極論、確率・統計が駆使できれば、自分で未来予測も立てれます!

「ムムムッ...!この企業の売上は上がる！」

なんて、データがなければ、そううまくいくものではありませんが、

例えば、まだ記憶に新しいコロナの感染者予想は統計的に出てくるものです。

統計から来る予測をもとに、旅行してもリスクは低いかどうか、

どれだけ経済を犠牲にするべきか、議論ができるわけです。

逆に、この統計の話もせずに議論を進めれば、とんちんかんな話になって終わるでしょう。

確率・統計は世の中の見方が変わる、イチオシの数学です。

ただ、残念ながら現在、統計は高校数学の範囲ではないのですが…。

人の直感に反する確率

なぜ、ものの見方が変わるといえるのか、

一つ例を挙げると、人の直感に反する確率が存在するからです。

有名なのは、「誕生日のパラドックス」でしょう。

具体的には、

「現在１つの部屋にn人の人がいるとする。

この時に、誕生日が同じ人がいる確率はいくらか。」、

あるいは

「何人の人がいれば、その中で誕生日が同じ人がいる確率が50％以上になるのか。」

という問題です。

birthday_party_woman_sunglass

あえて数学を用いずに、直感で考えてみるとどうでしょう？

一年は365日もあるのだから、誕生日が被る確率はかなり低そうに思えませんか？

その確率が50%を超えるには相当多くの人数が必要そうです。

極端なことを言えば、365日の1／2の183人が必要だと思う人もかなりいるのではないでしょうか。

答えの証明は読者に調べてもらうなりするとして…、

dac6a4cb42e8215ff87f1bd8c203f1e1_t

この答えはなんと23人です。

23人の人がいれば、少なくとも誕生日が同じ一組が存在する確率が50％を超える…、

言葉で納得するのは難しい、確率の妙です。

ちなみに、41人の人がいれば、90％以上の確率で、

70人の人がいれば、99.9％以上の確率で、誕生日が同じ人がいることになります。

これも、直感からずいぶんと乖離した結果ではないでしょうか。

一方で、この数値を100％にするには、

当然のことながら、366人（うるう年も考慮すれば、367人）必要ということになります。

最後のたったの0.1％のために、約5倍の人数が必要になるのも面白い点です。

確率において、100%を追及することがいかに難しいか、垣間見える例でもありますね。

稀な現象にも数学法則が働いている！

人の恋路を邪魔する奴は馬に蹴られて死んでしまえ！

こんな慣用句を聞いたことはありませんか？言葉通りの意味で、

人の恋路を邪魔するヤツは無粋の極みだから、往来を歩いていると、馬にでも蹴られるだろう、と。

馬が交通手段として、広く使われていたであろう昔でも稀な出来事だったのでしょうが、

こんな「馬に蹴られて」という事象を真面目に研究した人がいます。

ドイツの統計学者ボルトキーヴィッチは，

1875年から1894年までの間に200の騎兵隊を調べて「馬に蹴られて死んだ兵士」の数の統計を作ったそうです。

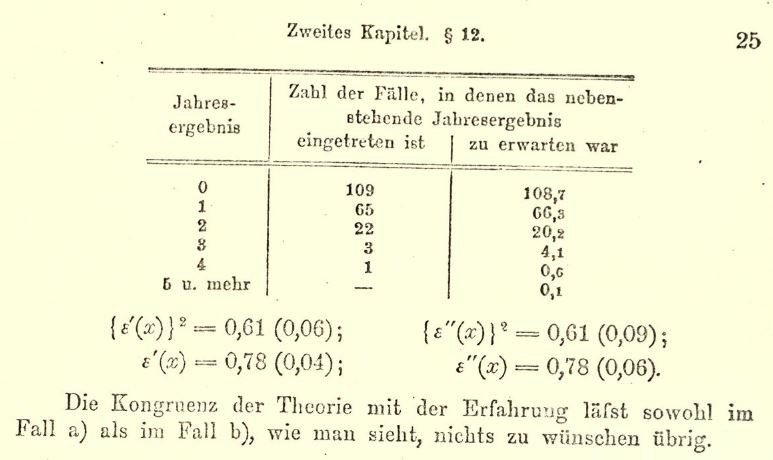
poison

引用元：Das Gesetz der kleinen Zahlen : Bortkiewicz, Ladislaus von, 1868-1931 : Free Download, Borrow, and Streaming : Internet Archive. (1898). Internet Archive. https://archive.org/details/dasgesetzderklei00bortrich/page/n85/mode/2up?view=theater

彼の統計によると一軍団あたりの死者の期待値は0.61人と、

軍団の人数に対して非常に低い数です。

こうした稀な事象にぴったりとあてはまる統計がありまして、ポアソン分布と呼びます。

例えば「30分に平均2回電話がかかって来るコールセンターにおいて、

1時間に6回電話がかかって来る確率」なんてモノも予測できてしまいます。

ポアソン分布が適用されるにはもちろん条件があるのですが、

その条件さえ満たせば、驚くほど正確に予測できるのです！

是非！詳しく調べてそのスゴさを眼にしてほしい！

まとめ

数学が秘めるスゴさ、魅力をお話しました。

c5119ed71378c337395bd69d7b814e53_t

もちろん、数字のポテンシャルも、面白さもこの記事では語りつくせないほど、

たくさんあります。

そして、多くの人が思っている以上に有用でもあるのです。

これを機に、数学がニガテな人も、「ちょっと数学の面白い話、調べてみようかなぁ」なんて思ってくれたらと思います。

そして...「数学やってみようかなぁ」なんて思ってくれたら...!

【PR】ぜひ一度、武田塾古市校にお越しください！！

武田塾古市校では、随時無料受験相談を承っております！！

武田塾古市校における無料受験相談の内容は、

〇志望校について
〇勉強の方法について
〇武田塾のシステムについて
〇勉強を行うことができる環境について

などが多くなっておりますが、これらの質問に1つ1つ丁寧にお答えをさせて頂いております！！