コーシー・シュワルツの不等式の使い方を例題を使って解説！

こんにちは！

海老名駅から徒歩7分の武田塾海老名校講師の鈴木です！

今回は，一度は聞いたことがある気がするけど結局覚えられない，覚えても使い所がわからないという人が多い

「コーシー・シュワルツの不等式」について解説したいと思います！

そもそも，コーシー・シュワルツの不等式ってなに？という方や，覚えられない！という方は，

コーシーシュワルツの不等式の証明とその覚え方を解説した記事がありますので，まずはそちらをご覧ください！

コーシー・シュワルツの不等式の証明と覚え方を解説！

上記の記事を読んでいただいた方は，コーシー・シュワルツの不等式を書きなさいと言われたらすぐに書けるようになっていると思います．

では，今回はコーシー・シュワルツの不等式の大学受験での使い方について，実際の過去問を使って紹介したいと思います．

この記事を読んでいただければ，受験数学においてひとつの武器になるコーシー・シュワルツの不等式を使いこなせるようになるはずです！

コーシー・シュワルツの不等式の使い方を例題を使って解説！
コーシー・シュワルツの不等式
コーシー・シュワルツの不等式の使い方
1. 例題1 早稲田大（2007年）
2. 例題2　東京大（1995年）
まとめ
1. 海老名駅周辺で塾・予備校をお探しなら武田塾海老名校の無料受験相談へ！

コーシー・シュワルツの不等式

まず，コーシー・シュワルツの不等式を復習しましょう．

$\begin{align*} (a_1 b_1 + a_2 b_2)^2 \le (a_1^2 + a_2^2)(b_1^2 + b_2^2) \end{align*}$

$\begin{align*} (a_1 b_1 + a_2 b_2+ a_3b_3)^2 \le (a_1^2 + a_2^2 + a_3^2)(b_1^2 + b_2^2 + b_3^2) \end{align*}$

という不等式が成り立つ．

等号成立条件は，それぞれ

$\begin{align*} a_1 : a_2 = b_1 : b_2 \end{align*}$

$\begin{align*} a_1 : a_2 : a_3 = b_1 : b_2 :b_3 \end{align*}$

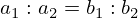
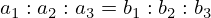
が成り立つことである．

より一般に，

$\begin{align*} (\sum_{i=1}^{n}a_i b_i)^2 \le (\sum_{i=1}^{n}{a_i}^2)(\sum_{i=1}^{n}{b_i}^2) \end{align*}$

が成り立つ．

このようになっていましたね，この不等式の使い方について，実際の問題を解きながら解説していきます！

コーシー・シュワルツの不等式の使い方

もう一度コーシー・シュワルツの不等式を見てみましょう．

$\begin{align*} (a_1 b_1 + a_2 b_2)^2 \le (a_1^2 + a_2^2)(b_1^2 + b_2^2) \end{align*}$

$\begin{align*} (a_1 b_1 + a_2 b_2+ a_3b_3)^2 \le (a_1^2 + a_2^2 + a_3^2)(b_1^2 + b_2^2 + b_3^2) \end{align*}$

この不等式とその等号成立条件は覚えているものとして例題を解いていきましょう．

ここで，aを定数，bを変数としてコーシー・シュワルツの不等式を書き換えておきます．

$(ax+by)^2\le(a^2+b^2)(x^2+y^2)$

$(ax+by+cz)^2\le(a^2+b^2+c^2)(x^2+y^2+z^2)$

このようにみて使うことが多いです．

例題1 早稲田大（2007年）

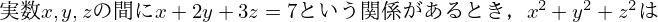
実数$x, y, z$の間に$x + 2y + 3z = 7$という関係があるとき，$x^2 + y^2 + z^2$は

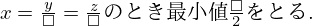
$$x = \frac{y}{\Box} = \frac{z}{\Box}$のとき最小値$\frac{\Box}{2}$をとる.$

この問題をコーシー・シュワルツの不等式を使わずに解くとすれば，点と平面の距離の公式を使うのがいいかと思いますが，

今回はその解法は省略して，コーシー・シュワルツの不等式を使う解答を紹介します．

解答

$コーシー・シュワルツの不等式\n $(ax+by+cz)^2\le(a^2+b^2+c^3)(x^2+y^2+z^2)$ $

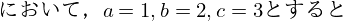
において，$a=1, b=2, c=3$とすると

$ 
(x+2y+3z)^2=(1^2+2^2+3^2)(x^2+y^2+z^2) 
$ 
となる．

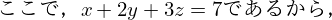
ここで，$x+2y+3z=7$であるから，

$$7^2 \le (1^2+2^2+3^2)(x^2+y^2+z^2)$

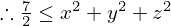
$\therefore \frac{7}{2} \le x^2+y^2+z^2$

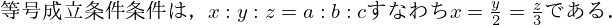
$等号成立条件条件は，$x:y:z=a:b:c$すなわち$x=\frac{y}{2}=\frac{z}{3}$である．$

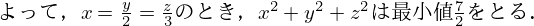
$よって，$x=\frac{y}{2}=\frac{z}{3}$のとき，$x^2+y^2+z^2$は最小値$\frac{7}{2}$をとる．$

この問題のように，

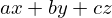
$ax+by+cz$

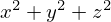
$x^2+y^2+z^2$

の2つの形が出てくる問題では，コーシー・シュワルツの不等式が使えるのではないかと試してみてください！

例題2　東京大（1995年）

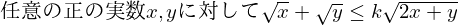
$任意の正の実数$x, y$に対して$\sqrt{x} + \sqrt{y} \le k \sqrt{2x+y}$$

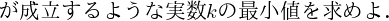
が成立するような実数$k$の最小値を求めよ．

この問題は一見コーシー・シュワルツの不等式の形とは異なる気がしますが，

実はコーシー・シュワルツの不等式はルートの和を上から抑えるときに使えます．

解答

$コーシー・シュワルツの不等式$(a_1b_1+a_2b_2)^2 \le (a_1^2+a_2^2)(b_1^2+b_2^2)$

$の両辺の平方根をとって，$a_1b_1+a_2b_2 \le \sqrt{(a_1^2+a_2^2)(b_1^2+b_2^2)}$が成り立つ．$

・ここで，右辺を問題の不等式の形に合わせていきます．

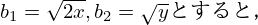
$$b_1 = \sqrt{2x}, b_2 = \sqrt{y}$とすると，$

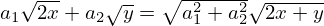
$a_1 \sqrt{2x} + a_2 \sqrt{y} = \sqrt{a_1^2 + a_2^2} \sqrt{2x+y}$

・ここで，左辺を問題の不等式の形に合わせていきます．

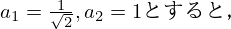
$$a_1=\frac{1}{\sqrt{2}}, a_2=1$とすると，$

$$\frac{1}{\sqrt{2}}\sqrt{2x} + 1 \sqrt{y} \le \sqrt{(\frac{1}{\sqrt{2}})^2 + 1^2} \sqrt{2x+y}$

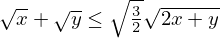
$$\sqrt{x} + \sqrt{y} \le \sqrt{\frac{3}{2}} \sqrt{2x+y}$

$$\sqrt{2x}:\sqrt{y} = \frac{1}{\sqrt{2}}:1$すなわち$y=4x$のとき等号が成立するので， $

$$k$が$\sqrt{\frac{3}{2}}$より小さいときは条件を満たさない． $

$よって求める$k$の値は$\sqrt{\frac{3}{2}}$である． $

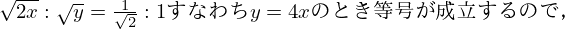
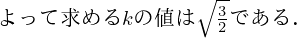
まとめ

今回は，コーシー，シュワルツの不等式の使い方を紹介しました．

・2乗の和と一次式を繋ぐ使い方

・ルートの和を上から抑える使い方

の2つを覚えておきましょう！

基本的な使い方を身につけておけば，不等式の証明問題や最大値・最小値を求める問題で使えることがあると思います．

海老名駅周辺で塾・予備校をお探しなら武田塾海老名校の無料受験相談へ！

今回は受験で使えるテクニックとして，有名不等式である「コーシー・シュワルツの不等式」を解説しましたが

そもそも受験に向けてどうやって勉強したら良いかわからない人もいるのではないでしょうか？

武田塾では生徒の「勉強のやり方」にアプローチする指導を行なっています。

それに加え、武田塾では「受験生を応援したい！！」と言う気持ちから、

この「勉強のやり方」を全て無料で公開しています！！！

「授業をしない」武田塾では、参考書を使って一人ひとりを毎日徹底管理するので、

サボれないので大変ではありますが、最も効率的に勉強すつことができ逆転合格を可能にします！

逆転合格をしたい！！と強い気持ちを持っている人にこそ向いている塾です！！

武田塾では無料受験相談を行っています！受験に関する不安や相談を全て無料で受け付けているのでぜひご連絡ください！！

塾をお探しの方へ

武田塾海老名校では毎日無料受験相談を実施しております。

受験に向けた勉強方法が分からない！

科目別の勉強法を知りたい！

など受験相談、勉強相談が必要な方！学力の上がる正しい勉強法を知りたい方！

是非、お気軽にお申込み下さい！お電話にて承っております。

受験相談は完全予約制。お気軽にお電話ください！

（TEL：046-240-1135）

－　・　－　・　－　・　－　・　－　・　－　・　－　・　－　・　－　・　－　・　－

また、武田塾海老名校に通っている生徒たちは、

旧帝大、を中心とした難関国公立大学や、早慶上理、医学部、獣医学部

中央大学、明治大学、青山学院大学、GMARCH レベルの大学を目指して頑張っています！

武田塾海老名校は、

１）正しい勉強方法を教える塾です！
２）勉強方法を教えて、あなたの志望大学に逆転合格できるまでの勉強計画をつくります！
３）その勉強計画に基づき、毎週宿題を出して、マンツーマンで徹底個別管理します！
４）毎週の成果は、”確認テスト”でチェックします！高得点がとれるまでやります！
５）絶対早く効率よく逆転合格することを目指します！
６）最短で合格するために、勉強のやり方や参考書の使い方までこだわって教えます！

もし、あなたが

学力の上がる “ 正しい勉強法 ” を知りたいのなら

目標とする大学へ最短で合格する方法を知りたいのなら

効率よく成績を上げる方法を知りたいのなら

是非無料の受験相談・勉強相談にお越しください！

無料受験相談・勉強相談は、一人一人のお時間を大切にしている為、事前の予約が必要です。

海老名の予備校・個別指導塾といえば

武田塾海老名校（逆転合格の1対1完全個別指導塾）

神奈川県海老名市中央2-4-40

第二東宝ビル2F

小田急海老名駅から徒歩6分

◆ お申込みは、こちらまでお電話ください！