コーシー・シュワルツの不等式の証明と覚え方を解説！

こんにちは！

海老名駅から徒歩7分の武田塾海老名校講師の鈴木です！

今回は，一度は聞いたことがある気がするけど結局覚えられない，覚えても使い所がわからないという人が多い

「コーシー・シュワルツの不等式」について解説したいと思います！

この記事を読んでいただければ，コーシー・シュワルツの不等式を書きなさいと言われたらすぐに書けるようになります！

ある証明に関連づけて覚えると自分で不等式の形が作れるようになると思いますので，一緒に見ていきましょう！

コーシー・シュワルツの不等式

$\begin{align*} (a_1 b_1 + a_2 b_2)^2 \le (a_1^2 + a_2^2)(b_1^2 + b_2^2) \end{align*}$

$\begin{align*} (a_1 b_1 + a_2 b_2+ a_3b_3)^2 \le (a_1^2 + a_2^2 + a_3^2)(b_1^2 + b_2^2 + b_3^2) \end{align*}$

という不等式が成り立つ．

等号成立条件は，それぞれ

$\begin{align*} a_1 : a_2 = b_1 : b_2 \end{align*}$

$\begin{align*} a_1 : a_2 : a_3 = b_1 : b_2 :b_3 \end{align*}$

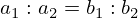
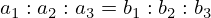
が成り立つことである．

より一般に，

$\begin{align*} (\sum_{i=1}^{n}a_i b_i)^2 \le (\sum_{i=1}^{n}{a_i}^2)(\sum_{i=1}^{n}{b_i}^2) \end{align*}$

が成り立つ．

こんな不等式を見せられてもなんのこっちゃと思ったあなた，大丈夫です．

この不等式をただ覚える必要はありません！

証明と一緒に覚えればこの式の形はすぐに思い出せます．

証明

まず，ベクトルを使った証明を紹介します．

$\begin{align*} \vec{a}, \vec{b} \end{align*}$

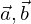
という2つのベクトルを考えてみましょう．

これらのなす角をθとすると，

$\begin{align*} \vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos{\theta} \end{align*}$

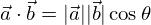
が成り立ちます．両辺を2乗して，

$\begin{align*} (\vec{a} \cdot \vec{b})^2 = |\vec{a}|^2 |\vec{b}|^2 \cos^2{\theta} \end{align*}$

となります．ここで，

$\begin{align*} \cos^2{\theta} \le 1 \end{align*}$

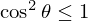
であることから，

$\begin{align*} (\vec{a} \cdot \vec{b})^2 = |\vec{a}|^2 |\vec{b}|^2 \cos^2{\theta} \le |\vec{a}|^2 |\vec{b}|^2 \end{align*}$

が成り立ちます．

2つのベクトルを成分で表すと，コーシー・シュワルツの不等式になります！

等号成立条件は，

$\begin{align*} \cos{\theta} = \pm 1 \end{align*}$

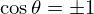
が成り立つとき，すなわち

$\begin{align*} \vec{a} // \vec{b} \end{align*}$

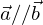
のときですね．

この証明を理解しておけば，コーシー・シュワルツの不等式とその等号成立条件をすぐに思い出すことができますね！

コーシー・シュワルツの不等式を使いたいときは，ベクトルの内積と大きさを比べているというイメージを持つと

不等式の形が思い出しやすいです．

ただし，nが4以上のときは2つのベクトルのなす角の定義がややこしそうです．

そこで，もうひとつ証明を紹介します．

$\begin{align*} \sum_{i=1}^{n}(a_i - b_i t)^2 = 0 \end{align*}$

という二次方程式を考えます．

この式の左辺は，0以上の数の和になっているので，xの値によらず0以上です．

したがって，この方程式の解は高々1個です．（二次関数のグラフをイメージしてみれば明らかです）

つまり，判別式Dは0以下になります．

実際に左辺を展開して判別式を計算してみましょう．

$\begin{align*} \sum_{i=1}^{n}(a_i - b_i t)^2 = (\sum_{i=1}^{n}{a_i}^2) - 2(\sum_{i=1}^{n}a_i b_i) t + (\sum_{i=1}^{n}{b_i}^2) t^2 \end{align*}$

になるので，

$\begin{align*} \frac{D}{4} = (\sum_{i=1}^{n}a_i b_i)^2 - (\sum_{i=1}^{n}{a_i}^2)(\sum_{i=1}^{n}{b_i}^2) \end{align*}$

になります．Dは0以上なので，

$\begin{align*} (\sum_{i=1}^{n}{a_i}^2)(\sum_{i=1}^{n}{b_i}^2) \le (\sum_{i=1}^{n}a_i b_i)^2 \end{align*}$

が成り立ちます．

等号成立条件は，すべての i = 1, 2, 3, ... ,nに対して

$\begin{align*} a_i - b_i t = 0 \end{align*}$

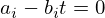
を満たす実数tが存在することです．

この証明はさすがに自分で思いつくのは難しいとは思いますが，なかなかエレガントな証明だと思います．

まとめ

今回は，コーシー，シュワルツの不等式の証明を紹介しました．

特に，ベクトルを使った証明は直感的にもわかりやすいですし，式の形を覚えやすいので覚えておくと良いと思います！

また，実際の受験でのコーシー・シュワルツの不等式の使い方についても解説をしたいと思います．

よろしければそちらの記事も読んでみてください．

今回覚えられた不等式をどのように使うか，解説しています！

コーシー・シュワルツの不等式の使い方を例題を使って解説！

海老名駅周辺で塾・予備校をお探しなら武田塾海老名校の無料受験相談へ！

今回は受験で使えるテクニックとして，有名不等式である「コーシー・シュワルツの不等式」を解説しましたが

そもそも受験に向けてどうやって勉強したら良いかわからない人もいるのではないでしょうか？

武田塾では生徒の「勉強のやり方」にアプローチする指導を行なっています。

それに加え、武田塾では「受験生を応援したい！！」と言う気持ちから、

この「勉強のやり方」を全て無料で公開しています！！！

「授業をしない」武田塾では、参考書を使って一人ひとりを毎日徹底管理するので、

サボれないので大変ではありますが、最も効率的に勉強すつことができ逆転合格を可能にします！

逆転合格をしたい！！と強い気持ちを持っている人にこそ向いている塾です！！

武田塾では無料受験相談を行っています！受験に関する不安や相談を全て無料で受け付けているのでぜひご連絡ください！！

塾をお探しの方へ

武田塾海老名校では毎日無料受験相談を実施しております。

受験に向けた勉強方法が分からない！

科目別の勉強法を知りたい！

など受験相談、勉強相談が必要な方！学力の上がる正しい勉強法を知りたい方！

是非、お気軽にお申込み下さい！お電話にて承っております。

受験相談は完全予約制。お気軽にお電話ください！

（TEL：046-240-1135）

－　・　－　・　－　・　－　・　－　・　－　・　－　・　－　・　－　・　－　・　－

また、武田塾海老名校に通っている生徒たちは、

旧帝大、を中心とした難関国公立大学や、早慶上理、医学部、獣医学部

中央大学、明治大学、青山学院大学、GMARCH レベルの大学を目指して頑張っています！

武田塾海老名校は、

１）正しい勉強方法を教える塾です！
２）勉強方法を教えて、あなたの志望大学に逆転合格できるまでの勉強計画をつくります！
３）その勉強計画に基づき、毎週宿題を出して、マンツーマンで徹底個別管理します！
４）毎週の成果は、”確認テスト”でチェックします！高得点がとれるまでやります！
５）絶対早く効率よく逆転合格することを目指します！
６）最短で合格するために、勉強のやり方や参考書の使い方までこだわって教えます！

もし、あなたが

学力の上がる “ 正しい勉強法 ” を知りたいのなら

目標とする大学へ最短で合格する方法を知りたいのなら

効率よく成績を上げる方法を知りたいのなら

是非無料の受験相談・勉強相談にお越しください！

無料受験相談・勉強相談は、一人一人のお時間を大切にしている為、事前の予約が必要です。

海老名の予備校・個別指導塾といえば

武田塾海老名校（逆転合格の1対1完全個別指導塾）

神奈川県海老名市中央2-4-40

第二東宝ビル2F

小田急海老名駅から徒歩6分

◆ お申込みは、こちらまでお電話ください！