今回は
『2024年 武田塾参考書ルート数学編』を
大公開していきたいと思います。

数学が苦手な人って多いですよね。
半分以上の高校生、いやもっと多くの受験生が苦手じゃないかなと。
「参考書で本当に成績が上がるの?」
と皆さん思っているとは思いますが、
成績が上がります!
今から紹介する参考書・特に数学が苦手な人に届いてほしい参考書がたくさんあるので、これらの参考書を極めてガンガン成績を上げちゃってください!
保証付きです!
【武田塾参考書ルートの構成】
まずは参考書ルートの基本の構成から話をしていきます。
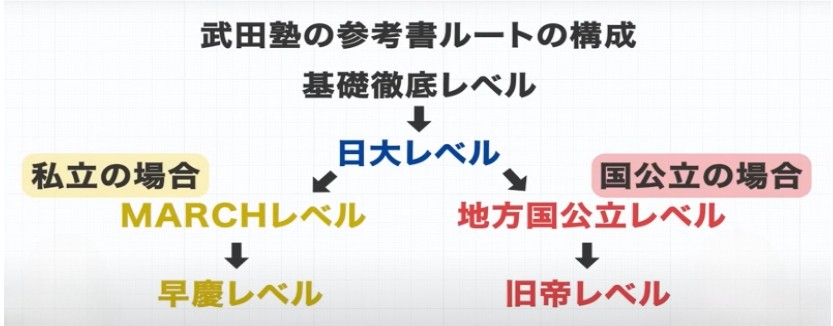
今回のルートから『基礎徹底レベル』というルートを設けました。
これは「学校の定期テストもキツいです・大変です」という人に向けた、定期テスト対策レベルと思ってもらえれば良いです。
普通に入れる人は『日大レベル』からですね。
多くの人は『日大レベル』からで大丈夫かなと思っているのですが、日大レベルのものに取り組んでください。
日大レベルのあとは、私立の場合『MARCHレベル』、国公立の場合『地方国公立レベル』MARCH・地方国公立のあとは『早慶レベル』『旧帝レベル』という形でルートを順番に進んでいってもらえたらと思います。

前半で文系、後半で理系について話をしていきますが、日大レベルまでは文系・理系共に使う参考書のシリーズは同じです。
なので理系の方も前半特に聞いてもらえたらと思います。
MARCH以降の文系と理系では使う参考書が変わりますので、理系の人はそこを飛ばして理系のところを見てもらえたら良いかと思います。
【基礎徹底レベル】
まずは基礎徹底レベルの話からです。
対象者は定期テストが結構赤点を彷徨っている人・平均点に届かないという人たちがやってほしいレベルになります。
基本的な問題から心配ですという人ですね。
「公式をまずは覚えましょう!」
「学校の授業についていくことがキツいです」
という人にぜひやってほしい本です。
日大レベルで『入門問題精講』シリーズや『基礎問題精講』シリーズというとてもおすすめの参考書を後ほど紹介するのですが、この『入門問題精講』や『基礎問題精講』を見てみてチンプンカンプンという人に取り組んでもらいたいレベルになります。

最初に使う参考書は、『やさしい中学数学』です。
その後、『やさしい高校数学』と『高校これでわかる問題集』を並行してやっていくというルートになります。
中学範囲もやっておいた方が無難です。
学校の定期テストでつまずく人は、
数学が昔から苦手だったという人が多い と思います。
今回中学校レベルになってますけれど、小学校レベルから復習しないといけない人も中にはいると思いますので、そういう人は小学校レベルからやってほしいです。
『やさしい中学数学』の良いところは、
中学3年間の数学を一冊で復習できる という点です。
3年分だとかなりの量に見えますが、そこまでかわらずササっとできます。
目安3週間ぐらいあれば十分に3年間の勉強を一冊で復習することができるので、高校受験の時に数学が苦手だったなという人は必ず復習しておいてほしいです。
英語や数学のような積み上げの教科は土台が厳しかったらまずはそこからやっていくことを無理せずに苦手な人はやってほしいと思います。
ここで次に高校の内容に入っていきますが、『やさしい高校数学』という本と『高校これでわかる問題集』という本を並行してやっていきます。『やさしい高校数学』はものすごく解説がわかりやすい本です。
『やさしい高校数学』は
・全数学嫌いに知ってほしい
・解説がものすごく丁寧
な本です。
「学校の先生が何を言っているのかわからなかった」
「聞いたことがあるけれど忘れた」
「まだ習っていないです」など、
そういうレベルでもこれを読めば最初の新しい単元の理解もできます。
数学Ⅰ・Aで2次関数という分野があります。
「2次関数とはそもそもこういうものだよ」という説明も載ってるし、
一問一問ごとの解説が非常に丁寧で「ここからここの式の変形はこういう意図で式を変形してるんだよ」とか
「2次関数のグラフとかもこんな風にグラフを考えようね」などを
余すことなく疑問が出ないように出ないように丁寧に説明してくれている参考書が『やさしい高校数学』なので、これで一問一問理解をしていって問題を解いていきましょう。
武田塾の数学の勉強で一番大事なことは
間違えた問題をできるまでやる! ことです。
全問正解するまでやるということがポイントなので、
『やさしい高校数学』も一問一問読んで終わりではなく、
ひたすらできるまで繰り返してください。

『やさしい高校数学』で解き方をマスターしたら、『これでわかる問題集』にチャレンジしていきます。
『やさしい高校数学』と『これでわかる問題集』を分野ごとに並行してやってください。
『やさしい高校数学』で2次関数を学び、そのあと『これでわかる問題集』の2次関数の問題を解くというやり方です。
『これでわかる問題集』の役割は何かと言いますと、
数学が苦手な人はある程度量をしないとダメ
だと思っています。
パターン化するまで、ある程度同じレベル帯で練習したいです。
『やさしい高校数学』もこれから日大レベルで登場する『入門問題精講』『基礎問題精講』も問題数をある程度凝縮してあります。
良くも悪くもなのですが、凝縮してあるということは苦手な人でも短時間でコンパクトに覚えられる、でも苦手な人からしたら経験して覚えたいじゃないですか。
いろいろなパターンをいっぱい解きまくって覚えるところが苦手な人からしたらありますので、その経験値を詰めるのが『これでわかる問題集』です。

『これでわかる問題集』の中身は完全にドリルみたいになっています。
難しすぎる問題は省いてあります。
よく学校で配布される『改訂版教科書傍用4STEP』や『サクシード』は意外と難しい問題が載っています。
難しい本はやらなくて大丈夫です。
『これでわかる問題集』は基礎の絶対に押さえてほしい問題を実際に何パターンか演習できるようになっています。
『やさしい高校数学』の解説で解き方をしっかりと身につけました、そうしたら『これでわかる問題集』で基礎の押さえてほしい問題を何度も解いて練習し、5回・6回同じことを繰り返したら
「やっと身についてきたぞ」「手が覚えた」みたいな、
そういう形で2次関数を制服して、その次に三角比を制服するという形で分野ごとに進めていってもらえたら苦手な人でも数学が身につくというような設計になっています。
定期テストでも全く同じ問題ではない可能性があるので、ある程度どんなパターンでも同じ単元のものであれば解けるという状態にできると『やさしい高校数学』だけよりは実力がつきます。
定期テストの範囲やこれからこの動画を観てくれている高1・高2生とかが
「今週この範囲が定期テストだ」ということが決まっていたら
『やさしい高校数学』と『これでわかる問題集』をやってもらえたら
平均点ぐらいは取れます。
差を分ける一問とかは、それこそ『チャート式』や『サクシード』など学校配布の問題集に載っていると思いますが、平均点を取るための基礎は身につきます。
これを分野ごとに進めていってください。
【日大レベル】
次に『日大レベル』について話します。
日大レベルをやる基準としては、進研模試で偏差値50以上で学校の定期テストは平均点以上取れていますという人は日大レベルからいきなり取り組んでもらって大丈夫です。

日大レベルで使う主な参考書としては『数学入門問題精講』シリーズ『数学基礎問題精講』シリーズという形で分野ごとに『数学入門精講』と『数学基礎問題精講』を使っていきます。

そのあとに、『ドラゴン桜式数学力ドリル』を計算練習として使っていきます。
Ⅰ・AならⅠ・A、Ⅱ・BならⅡ・Bというようにタイミングと合わせて使っていく形になります。

新課程の兼ね合いで『坂田アキラのベクトルが面白いほどわかる本』を『数学Ⅱ・B入門問題精講』の後にやることをベクトルが苦手な人に推奨しています。
『数学Ⅱ・B入門問題精講』にはベクトルがありません。

『数学Ⅱ・B基礎問題精講』+『坂田アキラのベクトルが面白いほどわかる本』が終わった段階で『大学入試数学落とせない必須101題スタンダードレベル』入れるようになってるのですが、『数学基礎問題精講』レベルの内容のアウトプットの目的で入れています。
文系の人はここで一旦終了で、理系の人は『数学Ⅲ・C入門問題精講』『数学Ⅲ・C基礎問題精講』という形で進んでいきます。

文系数学の場合、『数学Ⅰ・A入門問題精講』『数学Ⅰ・A基礎問題精講』これらと並行して計算力を鍛えるために『ドラゴン桜式数学力ドリル』をやります。
『数学Ⅱ・B入門問題精講』『数学Ⅱ・B基礎問題精講』『入門Ⅱ・B』と『基礎問Ⅱ・B』、の間にベクトルが苦手な人は『坂田アキラのベクトルが面白いほど分かる本』を間に入れます。これはカットしても大丈夫です。

理系の場合はその先ですね、『入門3・C』『基礎問3・C』という順番でやっていってもらえたら大丈夫です。

まず『入門問題精講』からどんな本なのか話していきます。
教科書の例題レベルのものを取り扱った問題集になっていて、各テーマの最初に「このテーマってこういうテーマだ」というようなテーマの概念から教えてくれて、問題と解説を繰り返して進んでいきます。
数学の本質が身につく一冊になっていて、苦手な人が絶対抑えておかないといけないこと・分かっておかないといけないことを解説してくれているので、丸暗記になりずらいというところが良いところです。
学校の授業で、とりあえずこの問題のパターンとこの問題のパターンと・・・みたいになってしまい、
「結局何をやっているのだっけ?」
ということが抜けがちな人はまずここから入ってもらうと整理されやすいです。
数学を今後上のレベルまで力を伸ばしていこうってなった時に表面的な理解では絶対に先につまずきます。
『入門問題精講』は文字が多いのでパッと見たら「うわぁ!」となりやすいと思います。
ですが、きちんと一つ一つ読み解いていき、かなりわかりやすく説明されているので、
読むということから逃げなければ理解できる内容 になっています。
この分野・この単元はこういうことがポイントなんだなという重要なところを解説してくれているので、
それをわかった状態で問題を解くということが非常に大事
です。
よく例に挙げるのは、
数学Ⅰ・Aの「場合の数」のところで、順列(P)の考え方と組み合わせ(C)という考え方があるのですが、数学が苦手な人は「これどっちだっけ?」と困惑してしまい、結局逆で考えてしまっていたりして計算ミスをしてしまうということがあるのですが、
これは『基礎問題精講』ではよくある話です。

『入門問題精講』では
こういう時は順列(P)で考える・こういう時は組み合わせ(C)で考える
そもそも場合の数はこういう考え方である
そもそも確率こういう考え方である
というように、考え方から説明されているので、
「なるほど、場合の数の考え方自体がそもそもこうなんだ」
「順列ってこう考えるんだ」「組み合わせでこう考えるんだ」
「 じゃあ実際に問題を解いてみよう、これはこういう場面なら絶対順列だ。」
「こういう場面だったら絶対組み合わせだ」
というように、わかった状態で一問一問解いてやるのが『入門問題精講』です。
次にやる『基礎問題精講』は、考え方の説明などはある程度省略されています。
学校の授業がある程度までついていけている・定期テストだったらある程度点数が取れてる人向けの本なので、そういう考え方が省略されているので、
『入門問題精講』の役割は非常に大事です。
考え方を学ぶという意味で取り組んでもらえたらものすごく良い効果を発揮すると思います。
単元理解をしっかりした上で基礎of基礎みたいな問題を『入門問題精講』で扱ったあとに、ある程度本格的な問題に『基礎問題精講』で入って定着を狙います。

次に『基礎問題精講』の紹介です。
この『基礎問題精講』を知らない人は絶対に知ってほしいです。
武田塾チャンネルの枠では『基礎問題精講』の話を年間千回ほどしています。

学校などで多く使われているのは『青チャート』シリーズ『Focus Gold』シリーズ、あと『4STEP』シリーズや『サクシード』シリーズや『3TRIAL』シリーズや『4プロセス』シリーズなど。
いろんな傍用問題集という本が配られていると思いますが、
僕らはそれ絶対にやめた方が良いよという話を武田塾の面談などでは毎回しています。
数学が苦手な人は特にです。
偏差値70以上の人は何を使ってもいいと思います。
だけど偏差値70未満の人は危険です!
『入門基礎精講』が解ける人は『基礎問題精講』からでも良いですが、黙って『問題精講』シリーズをとにかく使ってほしいです!
なぜかと言うと、学校で配られる問題集は量が多すぎます。
分厚い量・辞書みたいな量を一体何人の人が仕上げられるのか、
挫折率がものすごく高い!
です。
私たちは塾で働いているので、失敗してきた人をたくさん見ているわけです。
みんなは受験初めてだから
「大丈夫でしょ!いけるでしょ!」
と思うかもしれないけれど、やはりあの量は仕上げられないです!

武田塾は復習にものすごく力を入れています。
1周しただけだと全然力がつかないので何周もできなかった問題を繰り返してできるまで復習を繰り返してやるから数学は成績が伸びます。
あれだけ分厚い本を
何周もできる受験生がどこにいるんだ!
どれだけ時間があるんだ!
と思います。
基本は終わらないと思うので
薄い一冊『基礎問題精講』をきちんと仕上げるほうが成績は伸びます!
『4STEP』や『サクシード』はさらに最悪です。
解答・解説がほぼありません。
解答・解説が詳しくない本で勉強すると疑問点が沸きすぎて数学の勉強が詰まると思います。そういう意味でもおすすめではありません。
ということはわかっておいてほしいと思います。
なので『入門問題精講』とは逆の勉強になるので、使うとしても理解してある程度実力ついた後の計算問題集として使うという役割の本かなと思います。
『基礎問題精講』はそういう意味でまずは良いところで言うと
量がコンパクトです!
『チャート』や『FocusGold』の大体1/3ぐらいの量でさらに解説も詳しいです。
というところが『基礎問題精講』のおすすめポイントです。
同じように『基礎問題精講』は役割としてはインプットの本なので、一問一問きちんと解き方を理解しながら覚えていくという使い方をしてほしいです。
初見で考えすぎてしまう人がいるのですが、解き方は思いつかないので考えなくて大丈夫です。2〜3分考えてわからなかったら解答・解説を見てもオッケーです。
解答・解説をまず読んで理解をしてください。この問題はこういう風に解くんだなということをわかってください。
そうしたら必ず解答・解説を閉じて、もう一度自分で解答と解説を再現してください。
解答・解説が再現できたらその問題はクリアです。
必ず、正解できるだけではなくどうやってその解き方を思いついたのかという解き方の説明までできるようになってほしいです。
与えられた問題文の情報をヒントに
「問題文にこう書いてあるからこの考え方が使える」
「この解き方が使える」
「だから答えがこれになるんだ」
というように解答の1行目とかを、なぜその解き方を思いついたのか解答の方針を言えるようにする・説明できるようにするという部分にこだわって『問題精講』シリーズを進めてほしいです。

パターンで覚えてしまうと、模試で使えません。
『基礎問題精講』の問題が解けるだけでは意味がないです。
実際に模試・過去問・入試問題・初見の問題で使えるようになりたいです。
『基礎問題精講』で技を盗んでいくというイメージですね。
「こういう問題文・こういうヒントが与えられた・こういう条件の時はこの解き方が使える」
「違う条件・違う場面の時はこの解き方だ」というように
使う場面・状況と解き方をセットで覚えないと新しい問題になった時に使えないので、きちんと『基礎問題精講』では入試問題・初見の問題になった時に何をヒントにしてこの解き方を使うのかというところを絶対に押さえておいてほしいと思います。
なぜそうなるのかということを理解した上で濃い一問を絞った数でやるというところで、初見でも効果が出やすいのが『基礎問題精講』です。
・間違えた問題を全問正解できるまでやる
・4日進んで2日復習のペースを1週間で3回繰り返す
・解き方を説明できるようにする
この3点を守ってもらえたら数学の基礎はかなり力がつきます。

同時にやってほしい本として、『ドラゴン桜式数学力ドリル』がおすすめです。
こちらは計算練習用として使ってほしい本になります。
『基礎問題精講』はコンパクトな量で短期間で仕上がるので非常におすすめなのですが、計算量や演習量が不足してしまうという欠点があります。当たり前のようにできてほしい公式の計算とかはこの『ドラゴン桜式数学ドリル』でいっぱい解きまくって身につけてほしいです。
他の本だと、『受かる計算』シリーズや『試験時間と得点を稼ぐ最速計算』シリーズとか良い参考書が他にもあるのですが、『受かる計算』は計算が複雑すぎて「実際の入試ではここまで複雑な計算は出ないだろう」というレベルものも入っていたり、計算テクニックに寄っていたりするので、
純粋にたくさん公式を使う練習をしたいということでしたら『ドラゴン式数学力ドリル』が一番ベストな量になっていて良いということで採用しました。
サイン(sinθ)・コサイン(cosθ)・タンジェント(tanθ)でやはり計算につまずいてしまう人がすごく多いですし、
数学Ⅱ・Bで言うとシグマ(Σ)の計算や指数対数(log)の計算が複雑に感じている人が多いと思うので、
たくさん解いていくことによってそれを当たり前にできるようにします。
問題が難しくなると、
「このサイン(sinθ)・コサイン(cosθ)をどう変換するんだっけ?」
「logってどうするんだっけ?」
「シグマはどう計算するんだっけ?」など。
しかし、そこで止まっている時間はありません。
難関大を目指す人はその辺りの計算が当たり前のように秒でできるようにならないといけないので、秒でできるようになるためのトレーニングを『ドラゴン桜式数学力ドリル』で身につけてほしいです。
計算力をしっかりと準備しておかないと戦えないです。
『ドラゴン桜式数学力ドリル』はすごくコンパクトな量にまとまっているので、そこが一番の推しポイントなのですが、もっと演習量を確保したいという人は学校で配られている傍用問題集『サクシード』や『4STEP』などを使ってもらってもいいですし、計算力にさらに磨きをかけたいという人は『受かる計算』や『試験時間と得点を稼ぐ最速計算』シリーズを使ってもらうのも全然オッケーです。
数学が苦手な人に合わせて『ドラゴン流数学力ドリル』を採用しています。
ここまで、

『入門問題精講Ⅰ・A』『基礎問題精講Ⅰ・A』
『入門問題精講Ⅱ・B』『基礎問題精講Ⅱ・B』
と進めてきました。
『入門問題精講Ⅱ・B』の範囲の中にベクトルの範囲のみはなく、ベクトルは数学Cの内容になります。
『基礎問精講Ⅱ・B』が『基礎問題精講Ⅱ・B+ベクトル』という構成に新課程なっているので、『基礎問題精講Ⅱ・B』の場にベクトルが心配だよという人は『坂田アキラのベクトルが面白いほどわかる本』を加えてください。
『基礎問精講』から入試レベルまでベクトルの根本を教えてくれる参考書になっていますので、ベクトルの理解をしっかりと深めたいという人は入れてください。
なくても『基礎問題精講』のベクトルで十分いけますという人はいきなり『基礎問題精講』のベクトルでも問題ありません。

あともう一冊、『大学入試数学落とせない必須101題スタンダードレベル』も使っていきます。
この本は書いてある通り101題ありますが、数学Ⅰ・A/Ⅱ・Bの重要な問題、日東駒専レベルの問題を合わせて101題にまとめた本になっています。
『大学入試数学落とせない必須101題スタンダードレベル』は『基礎問題精講』と一緒にするのが一番ベストです。
『基礎問題精講』は他の参考書と比べると非常に良い本なのですが、そもそも数学の勉強の仕方自体が難しいですよね。
アウトプットを数字・文章が変わっても上手くアウトプットをしないといけないわけじゃないですか。
その問題は解けるようになりやすいので、
他の問題にしっかりと応用できるだけの力がついているのかということを確かめるための本として
『必須101題』をしてほしいです。
『基礎問題精講』で学習したことをアウトプットするための参考書になっています。
この『必須101題』を初見正当率が7割を超えていたら、『基礎問題精講』の内容が身についていた判定になります。
もし7割を下回って3〜4割ぐらいしかできていなかったら『基礎問題精講』の使い方が間違っている可能性が高いです。
つまり『基礎問題精講』を丸暗記してしまっていて全然理解できていないということです。
「2次関数のことは全然わからないけれど、とりあえず覚えました」
「一言一句覚えました」というような、
そういう感じでは『必須101題』で初見の問題を解いてみてくださいと言われると困るわけです。
実力チェック的な一冊として使ってほしいです。
『基礎問題精講』をインプットとするならば
『大学入試数学落とせない必須101題スタンダードレベル』はアウトプットの本ですね。
しっかりと実力がついているのか確認をして、この日大レベルを終えましょうという一冊になっています。
大事なことは、この『必須101題』で正答率が低かった時に
「もう終わりだ」とか「数学を諦めなさい」とか
そんな話はしていません。
もし『必須101題』で仮に正答率が4割だったとしましょう。
じゃあまず分野を確かめましょう。
どの分野が落としている割合が高いのか・分野によって偏りがあるのか
もし分野によって偏りがある場合は、『入門精講』『基礎問精講』でその分野を復習します。
復習をして明らかに理解不足なところがあれば、その範囲をしっかりと理解し直した状態でリベンジしてほしいです。
それができたら、落としている分野の例題や演習問題をもう一回解き直して、解けるようになっていたら、ある程度穴は埋まるのではないかなと思います。
なので、『必須111題』で苦手な分野を見つけ、その苦手な分野を『入門精講』『基礎問精講』でもう一回復習をして『基礎問精講』の演習問題までやれば苦手な穴は埋まると思います。
それでも心配な場合は、学校で配られるような『青チャート』や『FocusGold』などの類題を潰してみて穴が埋まるまでこの段階はじっくりと取り組んでほしいです。
以上が『日大レベル』でした。
理系向けの人にも少しお話しておくと、Ⅰ・A/Ⅱ・Bがしっかりと正しいやり方で初見の問題もアウトプット できるような力がついていないと数Ⅲ・Cはもっと難易度が上がるので、Ⅰ・A/Ⅱ・Bの段階でまず『必須111題』を解いてほしいです。
実力試し的な立ち位置になりますし、しっかりとクリアした状態で数Ⅲ・Cの勉強に入らないと、数Ⅲ・Cに入ってから終わった段階で
「勉強のやり方を間違えてるよ」
「数学を丸暗記だね」
「理解しながら全然解いてないね」
となったら1から全部やり直しになってしまうじゃないですか。
だからⅠ・A/Ⅱ・Bが終わった段階で『必須101題』をやってもらいたいです。
日大レベル全体を通しての進め方ですが、『入門Ⅰ・A]』『基礎問Ⅰ・A』『入門Ⅱ・B』『基礎問Ⅱ・B』『入門Ⅲ・C』『基礎問Ⅲ・C』、
『基礎問Ⅱ・B』が終わっ たら『必須100題』を入れたり『入門Ⅱ・B』が終わったら『坂田アキラのベクトルが面白いほどわかる本』を入れると話しましたが、さらに細かく進めていくやり方も高1・高2生はアリだと思っています。

『基礎徹底レベル』だと分野・単元ごとに話をしていきました。
ある程度できる受験性向けの進め方で高1・高2生は単元ごとに『入門精講』『基礎問精講』をやっておいた方が良いですね。
『入門』の「数と式」をしてから『基礎問』の「数と式」をしたり、
『入門』の「二次関数」をして『基礎問』の「二次関数」をするなど、
単元ごとに細かく分けて進めていったほうがしっかりと定着度を確認しながら進めていけますので、高1・高2生はそのやり方を特にお勧めしたいです。
ある程度学校の進度とかを踏まえながら今取り組むべき単元を横断してやっていくイメージです。
ただ、『入門精講』と『基礎問精講』の章が少し食い違っていたりするので、うまく対応してもらえたらと思います。
実力試しに、日東駒専の『過去問』を解いてみてきちんと力がついているかどうかを確認しながら次のレベルに進んでもらいたいと思います。
【文系数学MARCH・地方国公立レベル】
MARCHレベルも地方国公立レベルも基本的に使う参考書は共通なので、まとめて紹介します。

使う参考書は、
『文系の数学重要事項完全習得編』
『文系の数学実戦力向上編』赤・青の順でやってもらえたらと思います。
ここまででMARCH&地方国公立レベルが終了になります。

『文系の数学重要事項完全習得編』これも非常に良い本です。
このレベル帯で解説も非常に詳しくて例題が150題、演習も同じくらいの量ですが、150 題でⅠ・A/Ⅱ・Bの重要な問題をまとめてくれている一冊になっています。
本当に典型的な問題という感じですね。
入試の中でもこれは受験生は確実に取らないといけないという典型問題をまとめて押さえてくれていて、
解説が特に素晴らしく、必勝ポイントという形で
「こういうタイプの問題はこういう考え方で解いてください」というような解き方をまとめてくれているのが非常に良いポイントです。
是非その考え方を身につけるというイメージでこの問題を一問一問習得していってもらえるとすごく数学の力が伸びやすいと思います。
『基礎問題精講』がしっかりと仕上がっている人であれば『重要事項完全習得編』はスムーズに入れます。
人によっては赤から入る人もいなくもないですし、本当に時間がない時とかはそういう手段もありますが、基本的には『基礎問題精講』をやったあとで『重要事項完全習得編』の赤をやってもらうというイメージです。
MARCHの数学が易しめのところや、青山学院大学の全学部日程、あとは関関同立の関西大学と関西学院大学は比較的数学が易しいと言われているので、本当に時間がなかったらこの『重要事項完全習得編』だけで挑む人もいます。
よく言われるのは
「『基礎問題精講』と『重要事項完全習得編』は同レベルなのでは?」
「問題が被っているのではないか?」という疑問ですが、
『重要事項完全習得編』はどちらかというと
『基礎問題精講』の誘導を省いたバージョン
と思ってください。
『基礎問題精講』は誘導が丁寧です。

例えば「数列」の漸化式の問題ですね、上記のようなタイプの問題ですが
「まず(1)でこうしましょう」「(2)でこうしましょう」「(3)でこうしましょう」
という形なのですが、
実際は入試問題で(1)・(2)というような問題は出てきません。
いきなり(3)が(1)の問題として聞かれるのが入試の数学なのですが、『基礎問題精講』は誘導が丁寧めに苦手な人でも解けるように作られているので(1)・(2)が設けてあります。
補助輪付きみたいなイメージですね。
『基礎問題精講』はわりと丁寧めにまず文字を置くという、自分で文字を置かないといけないところをアシストしてくれています。
ですが『重要事項完全習得編』はそのような誘導は特にありません。
普通の入試問題に準拠して作られていますので、『基礎問題精講』が解けたからといっても、最後の問題だけ比べてみると同レベルの問題も多いのですが、『基礎問題精講』ほどアシストがありませんので
「『重要事項完全習得編』をさあ解いてみろよ!」というような感じで使ってもらえたら良いと思います。
余裕があれば演習問題もやりたいですが、時間がない受験生が多いと思いますので、やるとしたら例題をしっかりと固めてもらって例題の150題を身につけてほしいです。

次に『文系の数学実戦力向上編』ですね。
もちろん問題のレベルは上がります。
赤と青を比べてみるとやはり青のほうが難しいですが、この辺りの問題をしっかりと仕上げてもらえると、MARCH・関関同立・地方国公立は戦える範囲は広まります。
MARCH・関関同立は同志社大学の一部の難しい問題を除けば十分合格点を取れるようにはなります。
国公立も大学のランクで言うと難しいですが、神戸大学・筑波大学・横浜国立大学・ 千葉大学辺りが少し演習量が不足しますが、それ未満の大学や皆さんの地元の国公立とかは十分『実戦力向上編』をやれば戦えます。

では、先ほど挙げた神戸大学・筑波大学・横浜国立大学・ 千葉大学はどうすれば良いのかという話なのですが、『文系の数学』の例題だけではなく演習問題までやってもらったり『国公立標準問題集CanPass数学Ⅰ・A・Ⅱ・B・C[ベクトル]』を追加でやってもらうなど、この辺りまでやれば十分対策はできます。
ほとんどの国公立の大学は『実戦力向上編』までやれば十分だというように思ってください。
この参考書も赤と同じシリーズなので、引き続き解説が非常に詳しいです。
考え方重視の問題になっていますので、考え方を学ぶという意味で使ってもらえたらと思っています。
『重要事項完全習得編』と『実践力向上編』で過去の武田塾の生徒たちを見ていても良い使い方をしていると思うのは、
「この問題のポイントを一言でまとめるとこういうところ」というように
まとめを書いている人は伸びる傾向にあります。

今までの『基礎問題精講』とは使い方を分けて考えないといけません。
『文系の数学重要事項』や『実践力向上編』など、この辺りの入試問題集は、
「どうしたらこの解き方が思いついたのか」
「この問題のポイントはこういうところだよね」
という解き方・ポイントをまとめておくクセをしっかりとつけておいてもらえると、それが引き出しになって実際の初見の問題に使いやすいと思っています。
この話をする時に
「あなたが数学の参考書の著者ならどうするか」
という話をよくしますが、
例えば清水先生が大学に合格したころに戻ります。
数学もそれなりにやっていました。
高田先生が出版社をやりますね、「武田書店です」と。

「清水先生すごいですね。数学の実際に成績が伸びたようで。そんな清水先生に参考書を出してほしいのですが入試レベルの参考書をお願いしても良いでしょうか?」
というように頼まれたとします。
ただ本なのでページ数が限られています。
150問ぐらいで収めてほしいです。
「文系数学Ⅰ・A/Ⅱ・Bで入試でよく出るMARCHや地方国公立レベルの入試問題を150問ぐらいで本を作ってほしいです」
「問題数を絞る感じですね、300問じゃだめですか」
「いえ、150問でお願いします」
と言われたとします。
どのような問題を載せようか考えますよね。
実際に入試で戦える力をつけることを考えると、ある程度実践力がつく問題をチョイスし、その問題さえマスターしていれば汎用性がある、これは使えるという問題をチョイスするのではないですかね。
皆さんも150 問考えるとしたら
「二次関数で何問ぐらいだろうか?」
と考え、二次関数のその問題の中でも
「この一問で この考え方をマスターしてほしいな」
「次はこの 一問でこの考え方をマスターしてほしいな」
というように考えて150問をセレクトすると思います。
例えば二次関数で有名な問題だと、
最大値や最小値を求める問題や解の配置を求める問題やある程度有名な問題がありますよね。
「この考え方をマスターしておいてほしい」という問題がありますよね。
それをイメージしながら150問選ぶと思います。
つまり何が言いたいのかと言うと、
参考書には一問一問メッセージがあります。
そのメッセージに皆さんは気付くことができていますか?
問題をただの問題と思うのではなく、裏側にはなぜこの問題を収録しているのかという選んだ人の意図があるわけです。
この選んだ人の意図を感じながら、
「この問題のメッセージはこれだ!」
「入試問題でこういうパターンが出てきたらこう考えて解くんだ!」
というメッセージを受け取り、「この問題のポイントはここだ!」というようにメモをするクセをつけておけば数学力はグッと上がります!
出題者の意図を何も考えずに解いてしまうと、考えている人と比べて同じ二冊をMARCHレベル・国公立レベルでやっていてもかなり差が出てしまいます。
模試や入試問題で引き出しができていない状態です。
問題が出てきても「似たような問題を解いたことがあるが、どうやって解くのか忘れてしまった」というのは引き出しがない状態です。
一問一問「こういうタイプの問題はこう解く」という、「こういうプロセスだ!こういう考え方だ!」というようにメモをしておけば、しっかりと引き出しができている状態なので、入試問題で初見の問題であっても、「こういう問題はここが引き出しだよね」いうように「参考書のあの解き方を使うんだよね」というように解くことができます。
解き方・ポイントをまとめて、問題を見たらこの解き方となるようにしましょう!
そのことをしっかりと、この段階では丁寧にやってほしいです。
勉強法まで話すと長くなりますね。
先ほど少し話しましたが、MARCHレベルで演習量が足りない場合は追加でそれぞれ『重要事項完全習得編』の演習問題、『実戦力向上編』の演習問題まで取り組むとより良いと思います。

あと、似たような参考書として、『国公立標準問題集CanPass数学Ⅰ・A・Ⅱ・B・C[ベクトル]』が国公立でよく出る形式の数学の問題で、なおかつ計算が複雑な問題や『重要事項完全習得編』ほど綺麗ではなくて入試問題のような荒々しさを持った生の問題が載っていたりするので、『重要事項完全習得編』と『実戦力向上編』の二冊を終えた後に『CanPass』とかで演習問題までやっておくと、より国公立の中でも上位の国公立やMARCHの中でも難しい数学とかに対応しやすいと思いますので、追加でいくつか問題集を探している人は『CanPass』がおすすめです。
【早慶・旧帝レベル】
続いて、早慶・旧帝レベルで使う参考書は二冊です。

『大学入試問題集ゴールデンルート数学Ⅰ・A・Ⅱ・B応用編』と
『文系数学の良問プラチカ数学Ⅰ・A・Ⅱ・B・C』です。
メインは『プラチカ』です。
『プラチカ』は問題も抜群に難しいですが解説もかなり骨があるので、いきなり『プラチカ』に行く前に、まず『ゴールデンルート』を挟みましょうということです。

『ゴールデンルート』は全40題しか問題がありません。
かなりコンパクトな量になっています。
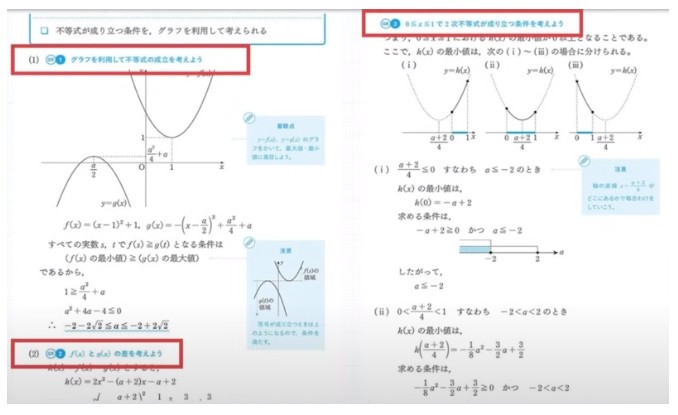
40題なので正解へのゴールデンルートという、問題のプロセスのようなアプローチ方法がまとめてありますので、これをみんなにはマスターしてほしいです。
早慶・旧帝レベルになってきますと2~3段階ぐらい操作が必要な問題が多いので、
「ある値を求めなさい」という問いがこの問題文に書かれていたとして、その値を求めるまでにまず中継地点としてこの値が絶対に必要で、けれどこの値を求めるためにはこの値が必要で、ではまずこの値を求めるためにはこうしよう・・・というような、2段階 か3段階ぐらい操作が必要で、もちろん融合問題などもあります。
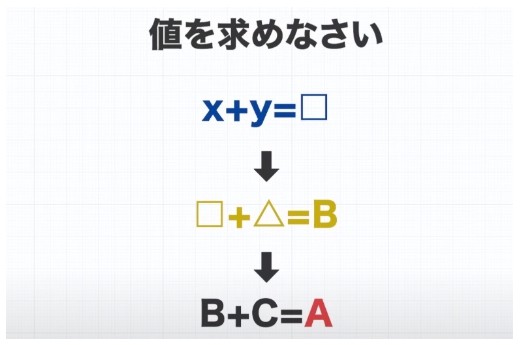
整数と〇〇の分野と〇〇の分野と確率など、いろいろと融合されている問題があるので、ダイレクトにその数値が求められることはないと思ってほしいです。
ゴールデンルートというその考え方の部分が必要で、この『ゴールデンルート』の参考書を通して、
この問題はまずこの値を求めて、次にこの値が出てきて最終的に求めたいこの値が求まる、
という全体の設計図みたいなものがこのレベルでは大事になってきます。
どういう段階で進めていくのかを全体の設計図をイメージし一歩目の動作に取りかかることができれば肥やしという風になります。
全体の設計図を意識する癖クセが身につく本なので40題を通してその詳しい解説をもとに技術を身につけてほしいです。

次に『プラチカ』に入ります。
早慶・旧帝大学の中でトップレベルに難しい大学、東京大学・京都大学・早稲田大学・慶応義塾大学もそうですけれど、その辺りの大学を受験する人は全部やってほしいのですが、時間がない人は最初からやるのではなく、優先順位をつけて出る分野から固めていった方が良いです。
「微分・積分」が数学Ⅱ・Bの範囲でよく出るのであれば、微分・積分をまずやってほしいですし確率がこの大学はよく出ますとなれば確率をやってほしいというように、自分の中で優先順位をつけて取り組んでもらえると良いと思います。
東京大学・京都大学・早稲田大学・慶応義塾大学・一橋大学や文系数学の中でもトップクラスの大学はもちろん全部やっておいた方が良いですが、大阪大学・名古屋大学・東北大学とかでしたら全部やるというよりは自分が得意にしたいところを選んでやった方が伸びると思います。
もちろん残り時間との兼ね合いもあります。
以上が文系数学です。
時間がほぼないケースでいきますと、
「『ゴールデンルート』だけやって受かりますか?」
と聞かれたら、うまくいけば受かるしうまくいかなければ受からないという確率論になってしまいます。
なので「だけで受かります」とは言えないです。
ただ時間がなくてそれが最善なのであれば、仕方がないという感じです。
残り時間の中で一番効率的にうまく活かせる方法があるのならば、
「地方国公立レベルレベルまで完璧です、『ゴールデンルート』をやりました。残った時間で『プラチカ』は全部は終わらないです。どうしたらいいですか?」
という質問に対しては
「『プラチカ』の最初からやるよりかは出る分野を選んでやるほうが合格の可能性は上がる」
という感じです。
早慶・旧帝レベルというレベル以上になります。
あとはどの大学にしても過去問演習は非常に大事ですし、国公立の場合は夏前に発表すると思いますが共通テスト対策もとても大事になってきます。
共通テストは共通テストで別で対策をしないといけないので、それはまた続報をお待ちください。
以上が武田塾の文系の数学ルートになります。
【理系数学MARCH・地方国公立レベル】
まずは理系数学のMARCH・地方国公立レベルの話に行きたいと思います。
使う参考書はこちらです。

『数学の良問問題集[数学Ⅰ+A+Ⅱ+B+Ⅲ]』 です。
数学Ⅰ・A/Ⅱ・B/Ⅲ・Cの重要な問題が300問載っています。
いくつかレベルがあり、必須問題・確認問題・レベルアップ問題というような形になっていて、レベルアップ問題がやや難しめの応用問題になっています。
一旦レベルアップ問題を飛ばして必須問題と確認問題を先に解いて、最後にレベルアップ問題をまとめてやるという形式が一番良いかなと考えています。
今までは過去のルートで話をすると、
『文系の数学重要事項完全習得編』『数学3重要事項完全取得編』『理系数学入試の核心標準編』この三冊を使っていたのですが、この3冊の役割を1冊にまとめて担ってくれている本が
『数学の良問問題集[数学Ⅰ+A+Ⅱ+B+Ⅲ]』になります。

それなら、まとめて『良問問題集300』をやろうという形になっています。
数Ⅲ・Cまでのあの膨大な量を入試問題は実戦を積まないといけないので、『良問問題集』は時間がかかります。
3つのレベルがあり時間がかかるので、理系の人たちは時間をかけてじっくりと仕上げてほしいと思います。
一冊で約3ヶ月くらいはかかるという本です。
『数学Ⅲ・C基礎問題精講』を一通り仕上げた人は、この『良問問題集』をじっくりと固めていくと、ある程度の国公立レベルアップ問題までやってもらえれば狙えます。
MARCHは基本的に全般大丈夫で、国公立でも神戸・横国・筑波・千葉以上の大学だと少し厳しいですが、それ未満の大学の金沢大学・岡山大学・広島大学辺りの国公立や皆さんの地元の大学は『良問問題集』で十分対応できるかと思います。
神戸・横国・筑波・千葉もレベルアップ問題までしっかりやって、あと追加で過去問演習を十分な期間が取れるのであれば合格点には乗せられると思います。
それくらい『良問問題集』は一冊で比較的幅広く対策できて優秀な一冊です。
解答・解説も非常に詳しいですし問題のチョイスが良いですね。
よく出る理系の典型問題を扱ってくれているな、という感じです。
石橋先生から見ても『良問問題集』は個人的にかなり使いやすい本だなといったところで、MARCH帯はなかなかこう参考書の設定が難しいところなのですが、とっつきやすいところから最終的に必要になるところまでをしっかりとまとめてあって、去年だと『重要事項』から『入試の核心』でつまずいていた人が結構いたみたいで、その辺りもステップアップしやすくなっている参考書かなと思います。
レベルの感じもとても秀逸な一冊になっているので、理系数学の新定番になるかなと思うので是非『良問問題集』に取り組んでほしいです。

MARCHレベルの追加の参考書としては『国公立標準問題集CanPass』がおすすめになってきます。
神戸・横国・筑波・千葉辺りの大学も、このあと旧帝レベルとして紹介しますが、北海道大学・九州大学辺りのレベル帯の人たちや、あとは明治大学の理系や東京理科大学・同志社大学の理系で難しい演習問題をもう少し積みたいという人たちは『CanPass数Ⅰ・A・Ⅱ・B・C[ベクトル]』『CanPass数Ⅲ・C』を取り組んでもらえたら良いと思っています。

あと分野で強化したいところがある人は『実戦数学重要問題集数学Ⅰ・Ⅱ・Ⅲ・A・B・C理系』のB以上のレベルの対策をするとその分野はかなり強化ができるのではと思います。
以上がMARCH・地方国公立レベルでした。
【旧帝・早慶レベル】
旧帝・早慶レベルは志望校別で使う参考書が変わります。
レベル帯によっては戦略別に使う参考書が変わります。
《東京大学・京都大学・東京工業大学・早稲田大学・慶応義塾大学》
一番上のフルスペック型の東京大学・京都大学・東京工業大学・早稲田大学・慶応義塾大学志望の話をまずしていきます。

MARCHレベルの『良問問題集』をした後に
『CanPass数Ⅰ・A・Ⅱ・B・C[ベクトル]』『CanPass数Ⅲ・C』
をやってください。
その後に使う参考書としては
『ハイレベル数学Ⅰ・A・Ⅱ・B・C[ベクトル]の完全攻略』 と
『ハイレベル数学Ⅲ・C[平面上の曲線と複素数平面]の完全攻略』 です。
同時平行か最後に過去問演習をやるという流れです。
時間がなければ『CanPass』はカットしてもオッケーです。
『ハイレベル数学Ⅰ・A・Ⅱ・B・C[ベクトル]の完全攻略』と『ハイレベル数学Ⅲ・C[平面上の曲線と複素数平面]の完全攻略』は難しい問題がたくさん載っているのですが、応用問題を戦う術・考え方を教えてくれる秀逸な一冊です。
歯ごたえ解き応えも非常にあり挫折する人もまあまあいますが、この参考書としっかり戦ってくらいついて応用問題の考え方を身につけてほしいという一冊となっています。
東大・京大・東工大・早慶志望は基本的に『ハイレベル完全攻略』をできれば全範囲をしっかりとやってほしいです。
この辺りで応用問題がどの分野で出てきても大丈夫な力をつけておくことが必要な力なのではないかと思います。
最難関大と戦うための武器をここで身につけるというイメージです。
東大理系の石橋先生でも『ハイレベル完全攻略』は非常に難しく、それなりに勉強をしていたつもりではありますが、やはり今見てもびっくりする難易度の問題が並んでいるなという印象を持っています。
ですが反対に言えば、これをしっかりと身につけることができれば、意外と本番の問題が簡単というところまで到達できると思いますので、上位大学を志望する人はしっかりと取り組んでほしいと思います。
解説の考え方の部分が受験生に特に身につけてほしいところです。
解説部分を読み解くのに非常に時間がかかると思いますので、一回読んでわからなくても少し期間を空けてやってみたり、できる人に質問をしたりなど、そのようにして確実に理解するところまで持っていってほしいです。
一問一問じっくりと身につけてほしいです。

同じレベルでいうと『やさしい理系数学』や『数学Ⅲ+C上級問題精講』などその辺りの参考書もあるので、解説の好みが分かれるところだとは思いますが『ハイレベル完全攻略』が一番人気といいますか、理系を極めたい人たちからしたら好きという感じの本です。
どれを使っても足りないということはないので、本当に好みだと思います。
というわけで『ハイレベル完全攻略』を最上位の人は使ってください。
《大阪大学・名古屋大学・東北大学》
阪大・名古屋・東北大学志望の人たちにおすすめしたい参考書を紹介していくのですが、ここで得点戦略別に使う参考書を分けたいと思います。
阪大・名古屋・東北大学志望の「高得点狙いの人」たちか「数学は確実に」タイプかで分けるのですが、「高得点狙いの人」たちは『CanPass』『ハイレベル完全攻略』『過去問』という順で進めてください。

過去問を始めるタイミングはもちろんいつからでも大丈夫です。
『ハイレベル完全攻略』と平行でももちろん大丈夫です。
『CanPass』は十分演習量が詰めている人はカットしても大丈夫ですし、『ハイレベル完全攻略』は全部一冊終わらせるのが厳しければ優先順位をつけて特にやりたい分野からやってください。
今回理系数学の話をしているので数Ⅲ・Cの出題割合が高いと思います。数Ⅲ・Cの微分・積分から優先してやるなどして組み込んでもらって大丈夫です。
「高得点狙い」がどういうことかというと、阪大・名古屋・東北大学も、例えば問題が6問出るとしまして、『良問問題集』の力で解ける問題もあります。
受験生なら絶対に落とせない問題ですね。
差をつける一問としては『ハイレベル完全攻略』のレベル帯の問題が出題されます。阪大で数学に特化して稼いで英語は苦手だから英語は低めにして逃げ切りたいという人は当然『ハイレベル完全攻略』を取って数学を武器にして逃げ切らないといけないわけですね。
なので『ハイレベル完全攻略』までやる必要はあります。

「数学は確実に」タイプの人は『良問問題集300』とかのレベルで取れる問題だけ取ってあとは英語や科学などで稼いで逃げ切るという、戦略でやる本が変わります。
「数学は確実に」タイプの人は『CanPass』と『過去問』をしっかりとやってください。
『CanPass』は『良問問題集300』とレベル的には似ていますので、『良問問題集 300』で学んだことを『CanPass』でアウトプットする演習の本として位置づけています。
数学で稼ぐか稼がないかによってしっかりやらないといけない人とやりすぎ注意な人に分かれていくということです。

考え方を鍛えたい人には『世界一わかりやすい阪大の理系数学合格講座』や論証が必要な問題や発想力を問われる問題など考え方を鍛えてくれる一冊になっているので、阪大志望に限らず名古屋・東北大学とかで応用問題の考え方や論証問題のアプローチ方法・記述の方法などを身につけたい人にはぜひやってほしいと思います。
《北海道・九州大学》
北海道大学・九州大学志望の人です。
『ハイレベル完全攻略』は基本的には必要はなく、そこまで難しい問題は出ないと思ってもらって大丈夫です。
たまに難しい問題が出る年もありますが、出たとしてもそこまで受験生のレベルに差はつかないだろうと思っています。

なのでやる本としては
『CanPassⅠ・A・Ⅱ・B』『CanPassⅢ・C』
あとは『世界一わかりやすい九大の数学』
この辺りをやってもらえたらと思います。
北海道大学志望の人でも『世界一わかりやすい九大の数学』をやってもらって大丈夫です。
北大・九州大に関しては『良問問題集300』だったり同じレベル帯の『CanPassⅠ・A・Ⅱ・B』『CanPassⅢ・C』この辺りのいわゆる入試の標準的な理系数学の問題がきちんと完成度高く仕上げられることが大事だと思います。
この辺りのレベルを丁寧に仕上げていくという方針で進めてください。
以上、理系数学最難関大レベル解説でした。
なかなか後半は一冊を完璧にすることが大変そうな参考書がラインナップになっていましたね。
『ハイレベル完全攻略』や理系のアウトプットの本は思考力を鍛えていく時間を大事にしてほしいと思っていて、わからなかったとしても諦めない気持ちで参考書に一問一問挑んでほしいです。
とにかく手を動かして実験をしてみるとか、そういう機会にしてほしいと思います。
時間的な焦りなどで答えを見てしまおうとなりがちだとは思いますが、そこですぐに答えを見ずに時間を決めてこの時間は絶対に考える・この時間でできる範囲でここまでできた・ここまではできなかったというところを自分なりにまとめても良いですし、そのようにやっていってほしいです。
考え方を鍛える期間がこの最難関大レベルだと思いますので、粘り強く取り組んで仕上げていってほしいです。
以上が旧帝・早慶レベルの参考書でした。
ここまでで数学が全部話が終わりますが、苦手な人でもしっかりと基礎固めをして数学が得意な人でも最初はやはり一問一問覚えるところからです。
「『基礎問題精講』2次関数でこんな解き方・考え方があるのか!」
というよう に一問一問解き方を身につけていくところからスタートします。
その武器を揃えた段階で、MARCH・地方国公立レベルの人は『良問問題集』や文系数学だと『文系の数学重要事項完全習得編・実践力向上編』そのあたりのいわゆる典型的な入試問題を一問一問『基礎問題精講義』で覚えた武器を使って解いていきます。
考える問題も出ますので、そこでしっかりと考えていきます。
最後の最上位は文系数学だと『ゴールデンルート』の応用編や『文系数学のプラチカ』や理系数学だったら『ハイレベル完全攻略』これはラスボスですね、この辺りはすごく考えさせられます。

難しいけれどここは折れずにグッと戦って
「いろいろな数値を当てはめてみよう」
「少し実験をしてみよう」
「グラフをいろいろなパターンで書いてみよう」
など、そうやって試行錯誤をして
「よし、この問題をこの解き方だったら解けるかも!」
という方法で解ける問題を一問でも増やしていく・考える回数を増やす、このようにしていけば苦手な人でも最終的に数学の点数が取れるようになるので、信じて諦めずにやってもらえたらなと思います。
ただどの教科よりも時間はかかります。
わりとテンポ良く、特に基礎を完成度高く仕上げるというところはやっていかないと、なかなか差がついてしまうかもしれないです。
英語と比べると参考書の冊数は減りますが、やはり一冊あたりのかかる時間が膨大ですが、武田塾はこれが一番効率の良いルートだと思っています。
学校で配られる本をけなした部分もありますが、世の中の数学の勉強法って非効率なことが多いので、効率を追求してもやはり時間かかる科目が数学なので、一番効率を追求したルートがこれだと思います。
【まとめ】
①2024年 数学参考書ルートで実力をつけよう!
②基礎をしっかり学び参考書ルートを完璧にしよう!
③完成度高く仕上げて志望校に合格しよう!
数学はしんどいですが粘り強く諦めずに一問一問丁寧に進めてもらえたら間違いなく伸びる科目なので、是非この参考書ルートを信じてやってもらえたら嬉しいです。
というわけで数学のルートこれで以上にしたいと思います。










