こんにちは!武田塾愛知日進校講師の高尾彩です!

センター試験まで残りあと少しですね。
残された時間はわずか、不安を感じる人も多いと思いますが、いままでの自分の努力を信じて頑張りぬきましょう!
***
ところで
今日は数学、主にベクトルの問題(センター試験なら大問4)で役立つ知識をブログに書きたいと思います。
ベクトルの問題では主に平面図形、或いは立体図形の問題が出されることが頻出ですが
みなさんどちらの方が解きやすいと感じますか?おそらく大勢の人は平面図形と答えると思います。
ではなぜ空間図形は解きにくいと感じるのでしょうか...?
それは、「正確な図形を描き起こすことが難しいから」
が、あげられると思います。平面と比べると単純に必要な要素が1つ増えていますから、これは当然だと思います。
そもそも図形にしないよーって人も、図形にしようとしてもうまく描けないよーって人もいると思います。
しかし、図形が絡む問題は、その図形を実際に描いて形や分かっていることを視覚的に確認することがとても重要です!
皆さん...
与えられた条件を元に、正確な立体図形を起こすことできますか?
そこで今回は…
早く!正確に!立体図形を描ける方法を伝授しちゃいます!!
これであなたも空間図形の座標を素早くとれるようになりますよ!
【数学ⅡB】立体図形のラクチンな書き方
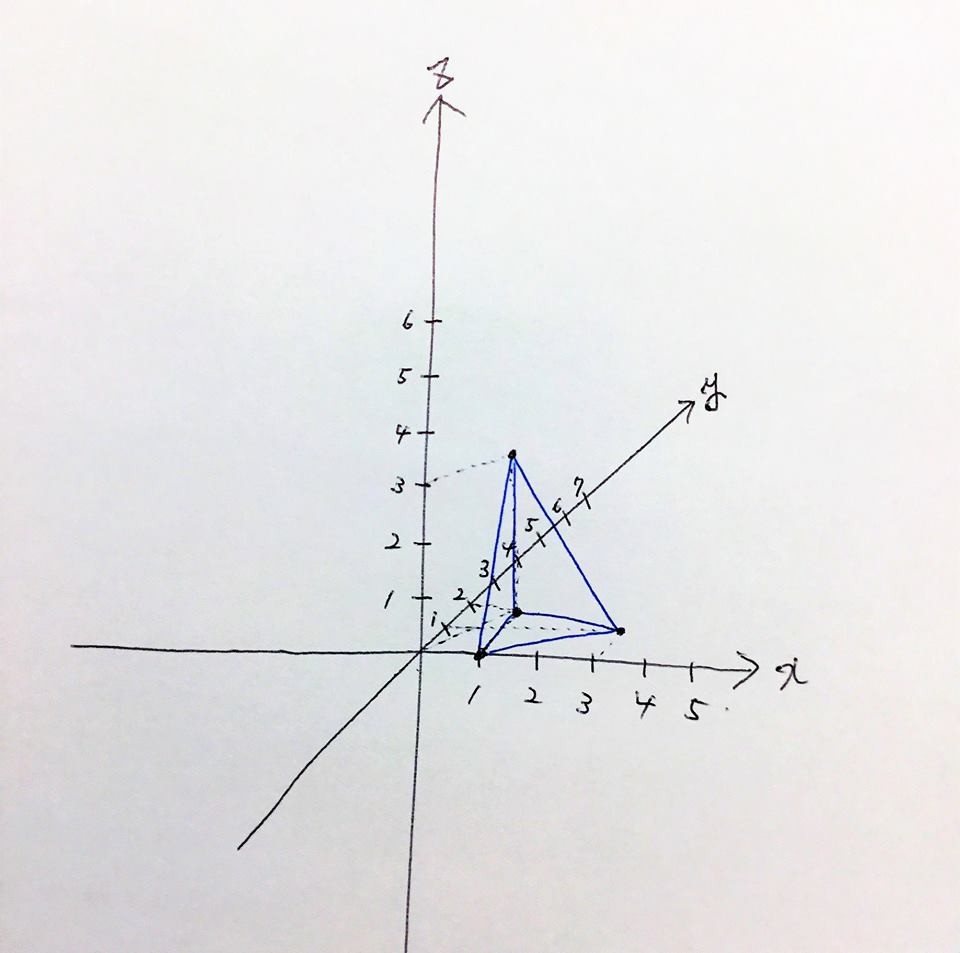
今回は例として(x,y,z)=(1,3,2)をとります。
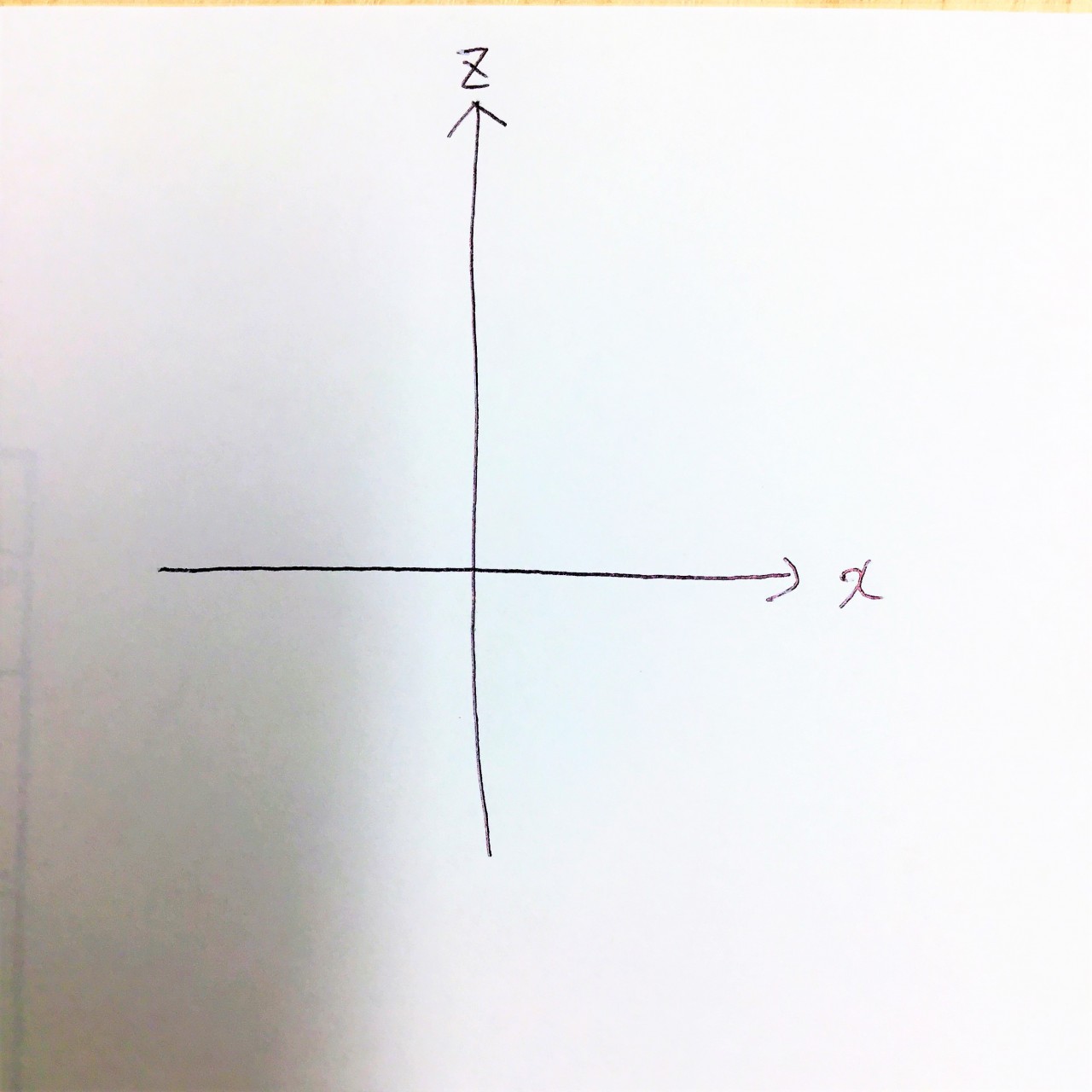
① 横にx軸、縦にz軸をひく
ここで縦にy軸を引くのではなくZ軸という所がポイントです!!
立体的に捉えるなら高さは縦に引いた方がわかりやすいですよね?
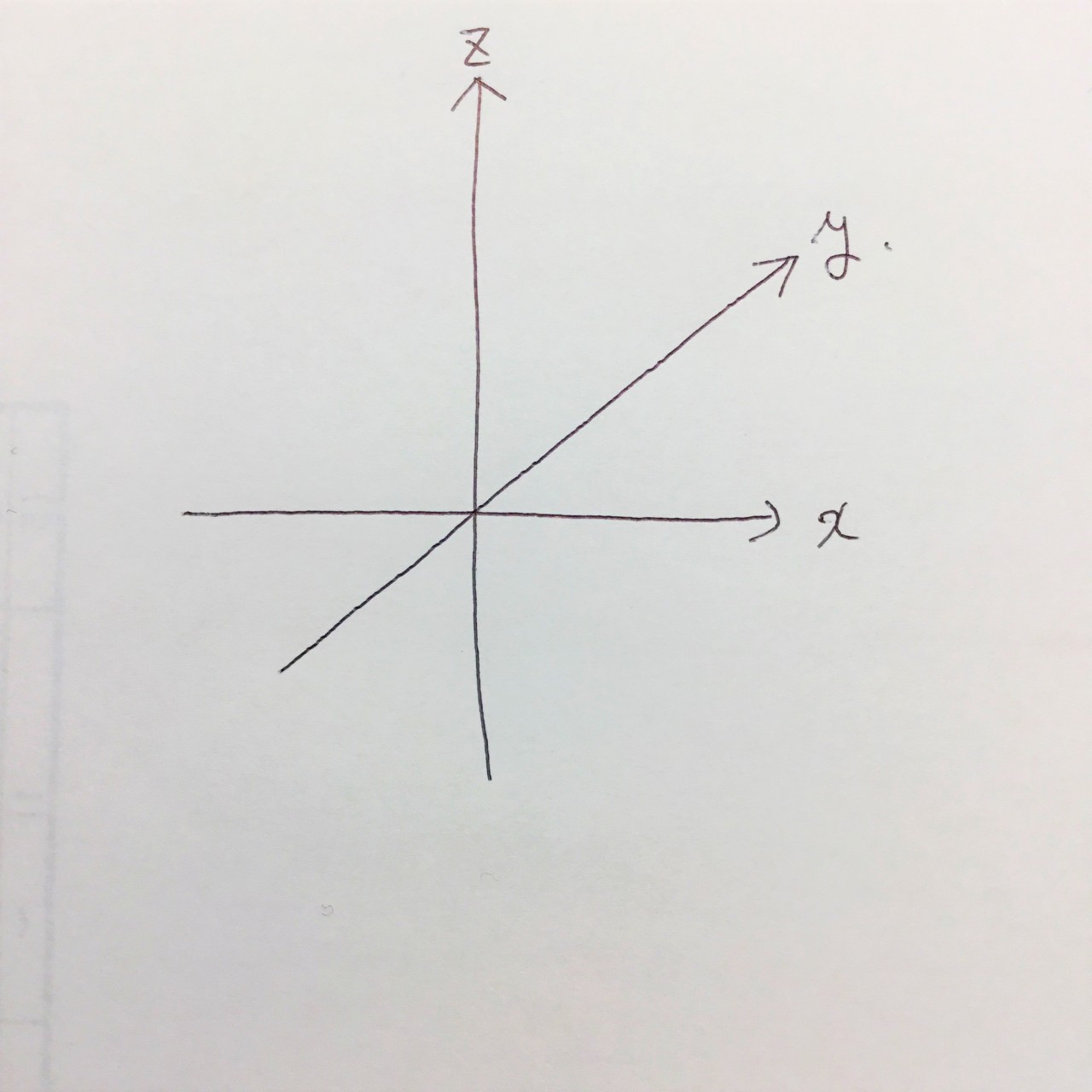
② ①で引いたx軸とz軸を45°で分けるように右上がりの直線(y軸)をひく
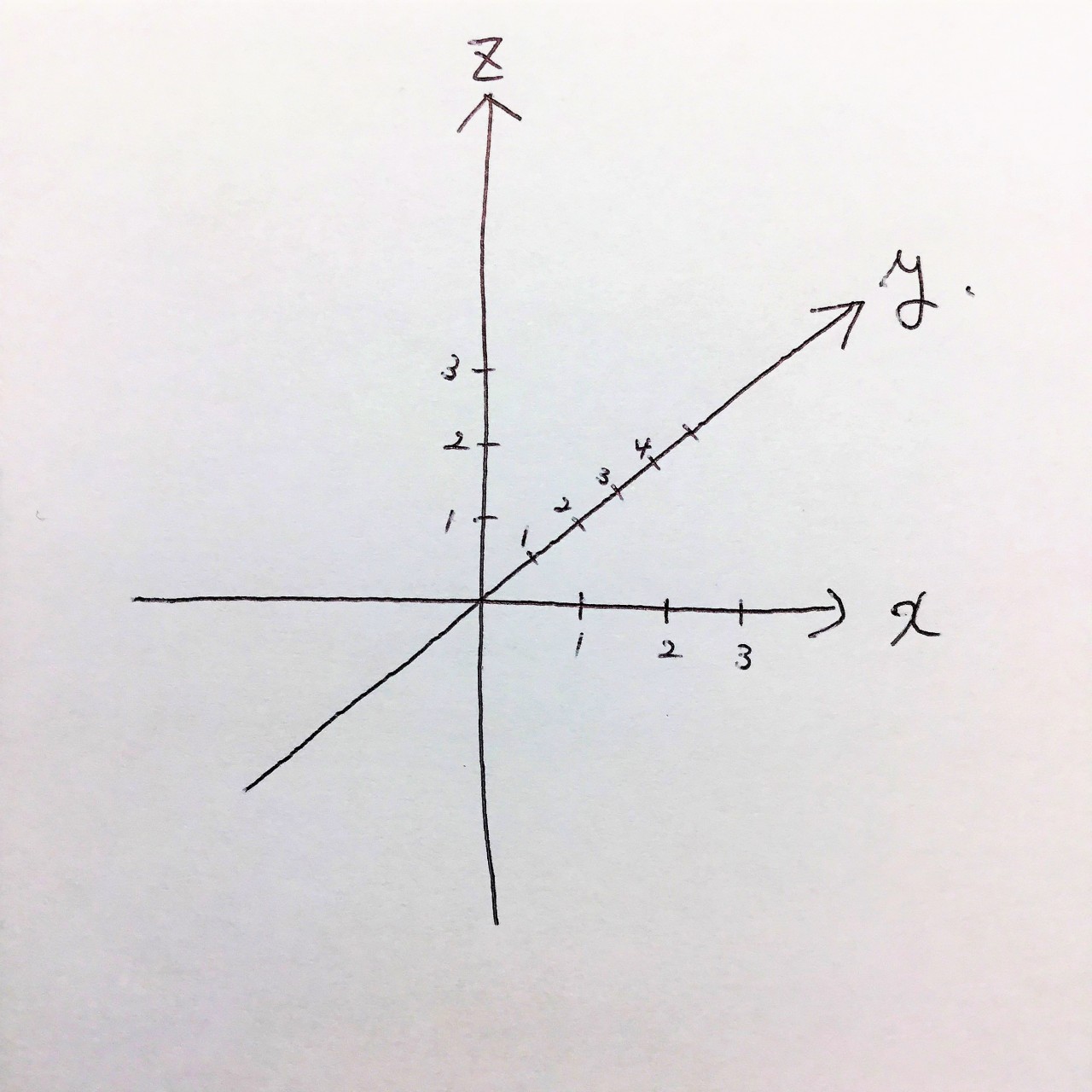
③ それぞれの軸に目盛りを付ける。(慣れてきたら目盛りは必要なくなります)
ここでの重要なポイントは、y軸の目盛りをx軸とz軸の目盛りの半分の長さにすることです。
このポイントを押さえるとよりリアルな図形を描けます。
④x-y平面上に(1,2)の点を取る。
この写真のようにそれぞれの軸に平行な直線の交点が点(1,2)です。

⑤ ④でとった点から、z軸と平行な直線を正の方向に伸ばします。
原点から点(1,2)にひいた直線と平行な線を点(0,0,3)から引きます。この2本の直線の交点が点(1,2,3)です。
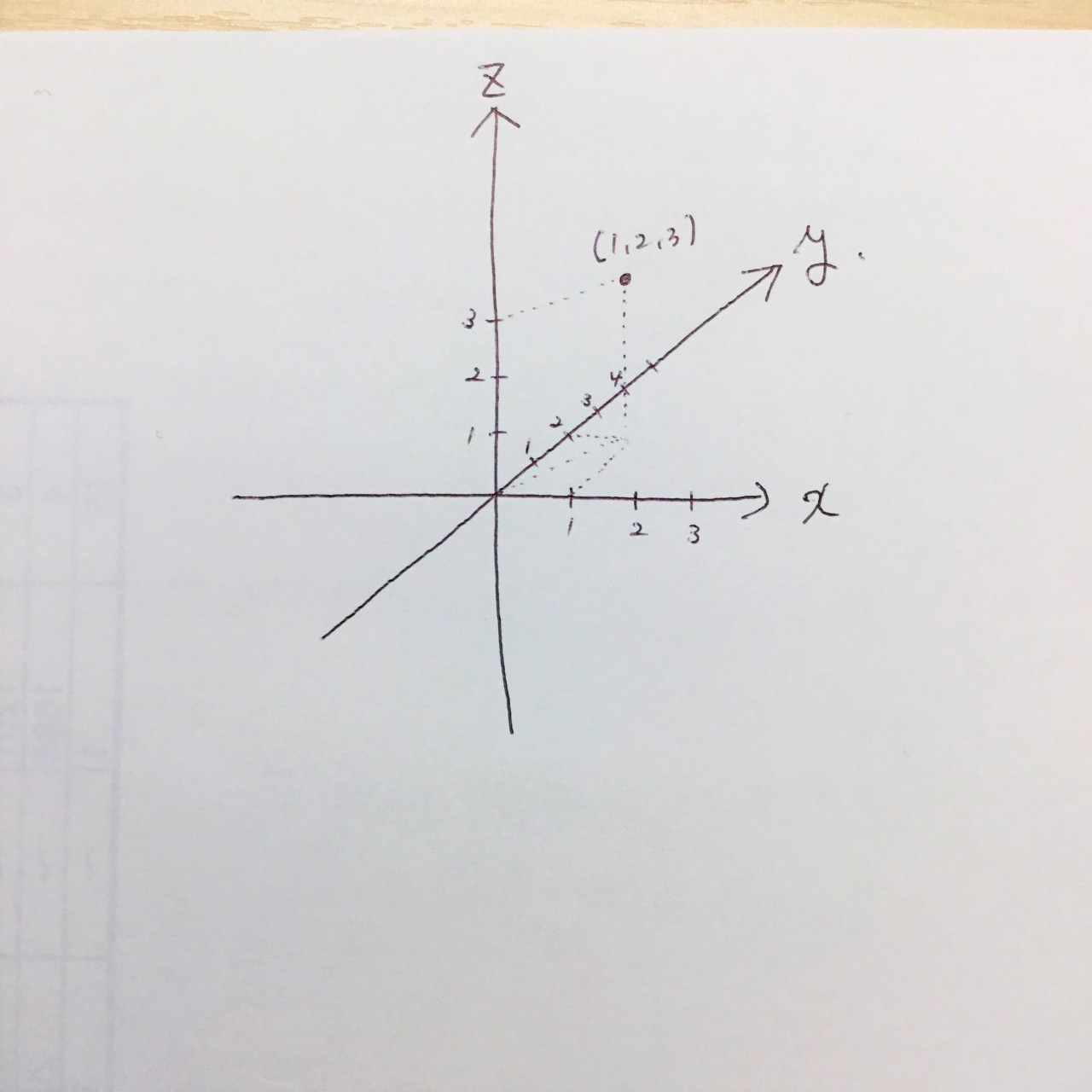
これで空間図形の点の取り方は完璧です!
この方法を使って一つの空間座標の中で4点とると、きれいな四面体を描くことができます。
見本で、(1,2,3)・(1,2,0)・(1,0,0)・(3,1,0) を頂点に持つ四面体を描きました。
***
どうだったでしょうか?
特に重要なのは①の縦軸をYではなく、Zでおくところが最大のポイントです!
これまでの癖で縦軸をYにしてしまいがちですが、これをZに置き換えるだけでぐっと図形が書きやすくなるはずです。
※ちなみに、縦軸をYにしてしまうと図形の形が分かりにくくなってしまう問題の代表として、
2014年度センター試験数学ⅡB 第4問 が挙げられます。
自分の作った図形が上手くいかず間違えた人...多いと思います!
是非作図しなおして解きなおしてみてください!












